基于反共振频率的复合材料损伤检测理论研究

哈尔滨飞机工业集团飞机设计研究所 何永亮 王 刚

东北大学理学院 李永强

目前，关于复合材料无损检测的方法有很多，但是每一种方法都有其自身的适用范围和局限性。本文旨在针对日益复杂的检测环境和不断提高的检测效率要求，研究一种既能满足外场检测环境和飞机部件原位检测要求，又能兼顾实用性和高效性的损伤检测理论。本文以复合材料结构动力学数据为基础，通过损伤引起的复合材料结构刚度变化而导致的动力学特性改变量为损伤检测依据，对复合材料进行损伤检测。

Yang和Lee[1]利用反共振频率对弹簧质量系统进行了损伤识别研究。Bamnios等[2]对裂纹梁结构进行了数值和试验研究，并利用得到的反共振频率成功地识别单裂纹损伤。Inada等[3]基于反共振频率成功对一复合层状悬臂梁进行了分层损伤识别。Dilena和Morassi[4]利用反共振频率变化对单裂纹自由梁进行了损伤识别。结论指出，该识别方法能有效地识别结构的损伤位置和损伤程度。

由于传统的损伤标识量均有其自身固有的缺点，而结构驱动点反共振频率在理论上兼具有振型和固有频率两者的优点，它既能在一定程度上反映结构的内在禀性，又能反映结构局部物理特性的变化，同时还具有与同阶的固有频率相近的测量精度。由此可见，结构驱动点反共振频率适合作为损伤标识量。由于目前应用反共振频率都是对梁结构进行损伤诊断，在复合材料蜂窝夹芯结构上的应用，从国内外文献上还未见报道。

1 反共振频率

振动系统中的反共振是一个对工程实际很有价值的概念。所谓反共振指的是弹性系统在某些特定频率的谐和激励作用下，系统某些部位出现谐和响应等于零的情形。换句话说，反共振情形也就是指在某些频率上系统某些部位的动柔度为零。那些出现谐和响应为零的频率就是反共振频率。

一般的无阻尼多自由系统在正弦激励下的频域运动方程为：

式中，K和M为分别为系统刚度矩阵和质量矩阵，f和x分别是输入和响应向量。

由式（1）可以求得位移导纳或位移频响函数为

式中，表示伴随矩阵，表示行列式。的第k，j项可表示为

式中，下标k，j表示矩阵的第k行、第j列已经被删去。则可得到多自由度系统的第k，j自由度的频响函数（或导纳函数）为

当k=j时，上式即为多自由度系统k点的驱动点频响函数（或驱动点导纳函数）。

令式（4）分子为0，即求解的特征值问题，可得到的频率即为第k，j自由度处的反共振频率。当k=j时，得到的ωr则为驱动点反共振频率。令式（4）分母为0，即求解的特征值问题，可得到多自由度系统的共振频率，即固有频率。而且对于n自由度系统驱动点导纳函数来说，其反共振频率数为（n-1），且与共振频率是一个接一个相互交替出现的，即两个共振频率之间必有一个反共振频率。

2 反共振频率对损伤敏感性分析

为了便于对多自由度结构系统进行敏感性分析，下面将引入模态坐标表示方法。为此，在谐振力激励下，多自由度结构系统的位移响应可表示为

式中，p为模态坐标向量，φ为振型向量矩阵，则有

式中

是由矩阵特征值组成的对角矩阵。因为有

则可令（φadj(Λ-ω2I)φT）的第kj项为零，由式（9）可得到导纳函数Hkj的零点（即反共振频率）。

对于任意的ω（包括ωr），(Λ-ω2I)i的行列式能展开为

于是对于第k，j导纳函数

利用式（10）可得到导纳函数表达式

考虑式（9）左边求和表达式中的一项，并让它对参数θ求导有

对上式右边第二项进行差分，然后代入式（9），经过重新整理可得到反共振频率的敏感性为

式中

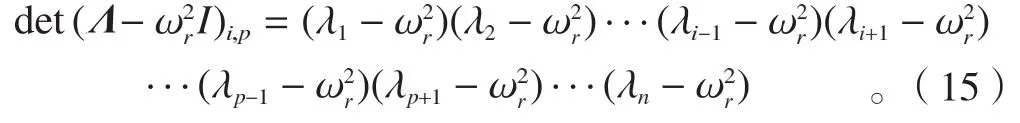
由式（14）可以看出，结构反共振频率的敏感性是其振型敏感性和固有频率敏感性的线性组合。结构反共振频率，特别是驱动点反共振频率在理论上兼具有振型和固有频率两者的优点，它既能在一定程度上反映结构的内在禀性，又能反映结构局部物理特性的变化，同时还具有与同阶的固有频率相近的测量精度。由此可见，结构反共振频率是一个重要的结构动力参数，对结构局部损伤敏感，适合用于结构损伤识别。

3 反共振频率对蜂窝板损伤分析

基于反共振频率信息的蜂窝夹层板结构冲击损伤识别方法的基本思想是：损伤的出现必然导致结构局部刚度的变化，从而引起蜂窝板结构各驱动点反共振频率发生不同程度的变化。通过获取蜂窝板结构各驱动点第一阶反共振频率曲面，与无损蜂窝板结构的各驱动点第一阶反共振频率数据比较，观察比较后曲面的突变来识别损伤发生，并对损伤进行定位及定量分析。

本文以铝制0.2m×0.2m，0.01m厚，蒙皮厚1mm，蜂窝胞元壁厚t为0.05mm，蜂窝胞元壁长l为6mm的蜂窝夹层板为模型，数值仿真模拟计算出各种损伤情况下蜂窝板各节点第一阶反共振频率值（本节中损伤程度以损伤面积D表示，D以蜂窝面积为单位）。

当蜂窝板存在芯层压溃损伤，损伤位于蜂窝夹层板中心位置时，随着损伤程度的增加，损伤对蜂窝板反共振频率差值的影响如图1所示。

当蜂窝板存在蒙皮脱层损伤，考虑损伤位于非中心位置（图2中凸起位置），随着损伤程度的增加，损伤对蜂窝板反共振频率差值的影响如图2所示。

由图1、图2可看出，数据图中较锐利的突起处与损伤位置完全符合，表明反共振频率法可准确地识别出蜂窝板的损伤位置。随着损伤程度的有规律增加，突起峰值点所对应的反共振频率差值也相应的规律增加，表明反共振频率法可判定蜂窝板的损伤程度。

下面考虑损伤位置改变时，反共振差值法对损伤识别的效果。当存在芯层压溃损伤，且损伤位置沿对角线由中心位置向边界斜向移动时，损伤对反共振频率差值的影响如图3所示。

图1 蜂窝板中心位置损伤程度增加反共振频率差值Fig.1 Effect of increased damage in the center position on honeycomb panel anti-resonance frequency difference

图2 蒙皮脱层损伤程度增加反共振频率差值Fig.2 Effect of increased skin damage on anti-resonance frequency difference

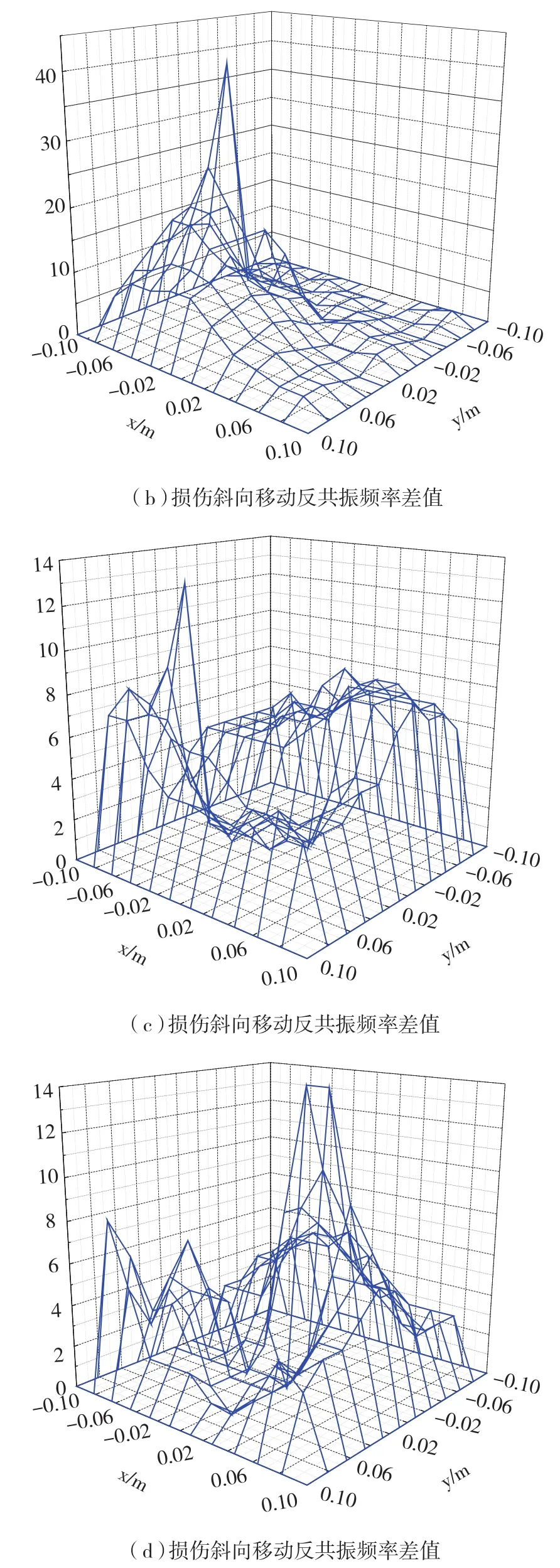
图3 损伤位置沿对角线方向改变时反共振频率差值Fig. 3 Effect of damage position moving on diagonally on honeycomb panel anti-resonance frequency difference

由图3可看出，由于边界效应，当损伤位置越靠近边界时，反共振频率法对蜂窝板损伤的判定效果越不明显。

4 蜂窝板损伤程度的定量分析

由于蜂窝夹层板的复杂结构所致，当损伤程度按一定比例增加时，其频率变化大都呈无规律变化，这给蜂窝夹层板的损伤程度识别带来很大困难。这里只对个别位置的个别损伤情况的损伤程度识别加以研究探讨。

在损伤形式、损伤位置判定正确的基础上，先以蜂窝夹层板中心位置处芯层损伤为例，其第2阶固有频率随损伤程度增加的频率变化量如图4所示（本节损伤程度以损伤蜂窝个数为单位）。

图4 蜂窝板中心位置芯层损伤第2阶频率变化量Fig.4 The second mode frequency variation of honeycomb panel with damage in the center position

从图4中我们可看出，各损伤对应的频率变化量与拟合直线能较好地吻合。通过图4所示3点数据可求得拟合直线方程如下：

其中，下标为相应数据点号。

通过式（16）可计算出损伤程度D。

由反共振频率定义可知，对于蜂窝板每个单元节点都有对应该点的反共振频率，故反共振频率反应结构局部性能的能力要强于固有频率，因此反共振频率可以更准确地反映蜂窝板损伤程度的变化。

中心损伤时损伤所在行单元各点随损伤程度增加的变化关系如图5所示，可见曲线峰值（即损伤位置反共振频率差值）近似等差递增。其损伤位置反共振频率随损伤程度增加的变化量如图6所示，得此拟合直线就可在损伤形式、损伤位置判定正确的基础上，只要计算出其与无损蜂窝板反共振频率的差值，就可准确计算出损伤程度。

5 结论

反共振频率法可有效直观地判定损伤位置，并具备损伤程度判定的能力。通过与笔者对蜂窝夹层板损伤检测研究的其他方法[5]（振型法、曲率模态法等） 相比较，反共振频率法较其他方法可更有效地识别蜂窝板各位置的损伤，这是本方法的突出优点。

图5 中心损伤所在行单元反共振频率差值Fig.5 Line unit anti-resonance frequency difference of increased damage in the center position on honeycomb panel

图6 损伤位置反共振频率变化量Fig.6 Anti-resonance frequency variation at damage location

[1]Yang S M, Lee G S. Structural damage identification using pole/zero dynamics in neural networks. AIAA Journal, 2001, 39(9)： 1805-1808.

[2]Bamnios Y, Douka E, Trochidis A. Crack identification in beam structures using mechanical impedance. Journal of Sound and Vibration,2002, 256(2)： 287-297.

[3]Inada T, Shimamura Y, Todoroki A, et al. Development of the two-step elimination identification method by resonant and anti-resonant frequency changes. Key Engineering Materials, 2004, 270-273：1852-1858.

[4]Dilena M, Morassi A. The use of ant resonances for crack detection in beams. Journal of Sound and Vibration, 2004, 276(1/2)： 195-214.

[5]张英杰,颜云辉,李永强,等.基于振型数据的蜂窝夹芯板损伤检测.东北大学学报,2012, 33(3)：418-421.