复杂交变载荷条件下微动运行状态

田帅，李欣，杨建伟，刘乐强，张育轩

复杂交变载荷条件下微动运行状态

田帅，李欣，杨建伟，刘乐强，张育轩

（北京建筑大学 机电与车辆工程学院，北京 100044）

研究典型的加载参数对复杂交变载荷作用下微动运行状态的影响。利用ABAQUS建立了二维（平面应变）有限元模型，模拟微动垫和试件在循环法向载荷和轴向载荷下的接触状态，对不同加载条件下的微动运行状态进行分析，提出一种曲线的分析方法，再结合双轴微动疲劳试验验证其适用性。比例加载条件下，在微动垫夹具刚度较小时的t的曲线为直线，而微动垫夹具刚度较大时的t曲线表现为不规则的四边形，这些条件下的曲线均为线性函数，并且随着微动垫夹具刚度增加，曲线的斜率增大；非比例加载条件下，t-曲线的形状不再是四边形，形状较为复杂，此时曲线为椭圆函数。随着微动垫夹具刚度的增大，椭圆的短轴增加。当相位差不为90°时，椭圆两半轴与坐标系不平行，椭圆发生旋转；特别地，相位差为90°时，曲线为标准椭圆函数。当曲线与直线=±相交时，由于滑移的产生，椭圆曲线将发生变化。在复杂交变载荷作用下，不同的加载参数（法向载荷、轴向载荷、微动垫夹具刚度等）或其相互间的组合会影响曲线的大小和位置，提出的曲线方法可以为分析复杂交变载荷条件下的运行状态研究提供手段，为进一步地讨论微动疲劳或微动磨损行为提供指导。

微动；多轴交变载荷；动力学；接触状态；有限元仿真

微动是指在交变载荷的作用下，两个相互接触的表面之间发生微小滑动而引起的磨损和疲劳现象[1]。微动常见于各种紧固连接的结合面上，由微动磨损导致接触表面的损伤，在交变载荷作用下，结构更容易发生疲劳破坏。相同试件的疲劳试验，存在微动作用时的疲劳寿命比不存在微动作用时的疲劳寿命降低30%～50%[2-4]。

航空发动机叶片和轮盘一般采用榫连接结构，这是一种接触结构的连接形式[5-6]。在发动机工作过程中，叶片受到离心力、气动力、振动等复杂的载荷作用，使叶片根部的榫头与轮盘的榫槽之间产生微小的运动，造成两者接触界面上的微动疲劳[7-9]。榫连接结构是航空发动机故障的多发部位之一，微动疲劳会加速榫连接结构接触部位裂纹的萌生和扩展，大大降低零件的疲劳寿命[10-11]。显然，在飞行过程中，轮盘和叶片接触界面之间的法向载荷不断变化，这意味着微动通常发生在多轴可变载荷条件下。一些研究者注意到了这一局限性，并进行了相关研究。

米雪等[12]通过690合金管/405不锈钢块（线接触）的切向微动试验，探究了690合金管在不同法向载荷作用下的切向微动磨损机制和损伤演变规律。景鹏飞等[13]在不同的载荷和位移幅值下，结合微动图以及不同微动接触状态和滑移状态下材料的损伤机理，得出切向摩擦力、微动振幅是影响微动磨损的重要因素。石炜等[14]在自行设计的微动疲劳试验装置上进行了各向异性材料的微动疲劳试验，分析了轴向和法向应力对微动疲劳寿命以及微动接触区最大等效应力、滑移幅值、法向应变幅值等微动疲劳参数的影响。

Peteghem等[15]研发了双伺服液压执行器试验系统利用微动磨损试验，通过控制切向位移和法向载荷研究了恒载荷和变载荷条件下的磨损过程和磨损动力学。Fouvry等[16]讨论了接触区尺寸、频率和循环法向载荷对微动裂纹形状和磨损率的影响。Abbasi等[17-18]研究了接触压力以及轴向和法向接触载荷之间的相位差对循环法向接触载荷条件下Al7075-T6 微动疲劳行为的影响。Liao等[19]研究了合金690在285 ℃纯水中不同法向载荷下的微动腐蚀疲劳行为，研究表明随着法向载荷的增加，疲劳寿命降低，表面损伤和亚表面变形更加严重。Sun等[20]开发了一种新型的高温摩擦疲劳试验装置，研究了镍基单晶（NBSX）超合金在高温下的摩擦疲劳机制，在600 ℃下进行了5种加载条件的疲劳试验，发现摩擦疲劳寿命随着轴向载荷和法向载荷的增加而降低。

目前大部分的研究工作都集中在可变切向力与轴向载荷的组合上，然而，许多实际工况下，广泛存在着可变法向载荷和轴向载荷的多轴加载条件，因此，本文在传统微动疲劳模型分析的基础上，讨论了受循环法向载荷和轴向载荷作用的修正微动疲劳模型的接触行为，重点研究了法向载荷和轴向载荷的相位差、微动垫夹具（“弹簧”）刚度等对微动动力学和接触状态的影响，提出了一种曲线分析方法，研究复杂多轴交变载荷条件下微动运行机制。

1 微动疲劳研究模型及动力学分析

1.1 研究模型概述

微动疲劳是燕尾接头、螺栓接头、花键接头等机械接头的主要失效形式之一[21-22]。几十年来，许多研究都集中在这个问题上，并逐渐形成了一个统一的研究模式。如图1a所示，2个圆柱形微动垫靠在一个扁平的试样上，他们之间通过一个恒定的法向载荷形成接触。同时，微动垫的固定装置可以被当作一个“弹簧”来抵抗微动垫的运动。然后，在“弹簧”和施加在试件下端部的轴向载荷的共同作用下，会产生一个可变的切向力，因此，在微动垫和试件的接触区域中产生了微动效应，该模型已被广泛用于研究微动疲劳和磨损机理，基于该模型，研究者们进行了一系列的试验和仿真。但是，该模型仍有一定的局限性，不能完全反映实际工况下的微动条件。

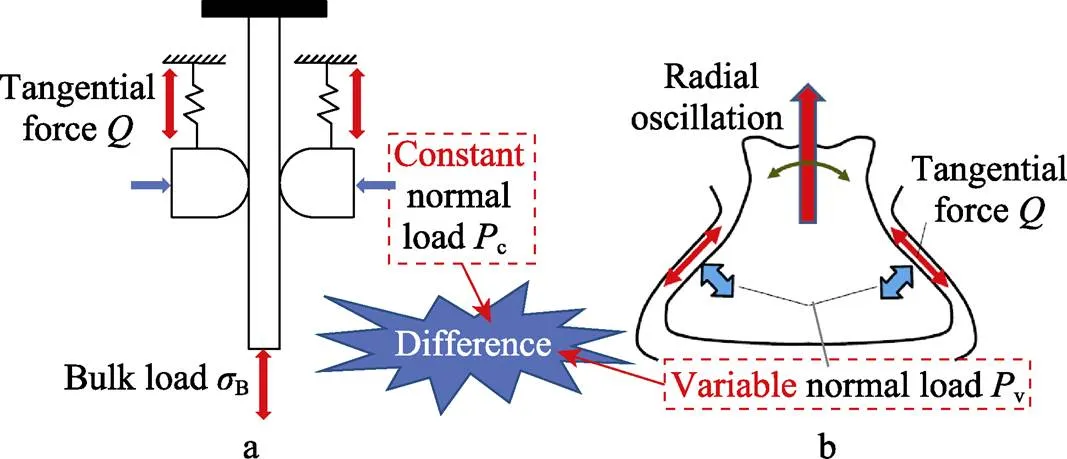
图1 当前的微动疲劳模型（a），实际航空发动机燕尾榫工况的载荷模型（b）

一个典型的例子如航空发动机燕尾接头的微动问题，如图1b所示。在飞行中，发动机榫连接处的法向载荷不断变化，与恒定法向加载条件下相比，实际微动系统的动力学和接触应力分布有很大的不同。

Barber等[23]研究了周期性法向载荷和切向载荷下的接触情况，并给出了分析接触状态的解析解。Hojjati-Talemi等[24]建立了有限元模型，分析了变法向载荷和切向力作用下的应力分布。

1.2 微动动力学分析

微动疲劳模型各部分的位移如图2所示，其中“弹簧”（微动垫夹具）的刚度为f，试件的刚度为s。点和点是在接触区中心的2个对应点。这两点的位移量分别为和。s为试样的整体位移。将定义为与点在试样中的位置相关的参数，α=δ/s，则=αδs，1。切向力可描述为：

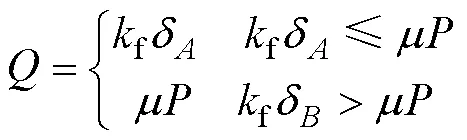
式中：为微动垫与试件的摩擦因数；为施加在微动垫上的法向载荷。

图2 微动疲劳模型示意图

Fig.2 Schematic diagram of fretting fatigue model

运动过程如图3所示。如果在试样的末端施加周期性的轴向载荷B，试件和“弹簧”开始变形。当加载循环开始轴向载荷B较小时，接触区中心处于黏滞状态，即点和点具有相同的位移和切向力，f=kf。在、||<||的条件下，随着B的增加，接触状态由部分滑移变为完全滑移。在部分滑移情况下，点和点始终具有相同的位移；在完全滑移情况下，微动垫在第一个循环中调整其相对位置，并在点移动到一个新的平衡位置，然后随着轴向载荷的变化，其平衡位置将在第二个循环中保持稳定或再次改变。

在上述分析中，没有考虑法向荷载的变化，如果考虑到法向载荷的变化，接触状态将会非常复杂。由式（1）可知，当接触状态在整个周期内保持部分滑移时，切向力不受法向荷载变化的影响，仍与轴向荷载呈线性关系，而在法向载荷和轴向载荷的作用下，微动垫会移动到一个新的平衡位置或不断变化，这种情况下的运行状态模式与正常的恒定完全滑移条件相似，但更复杂。

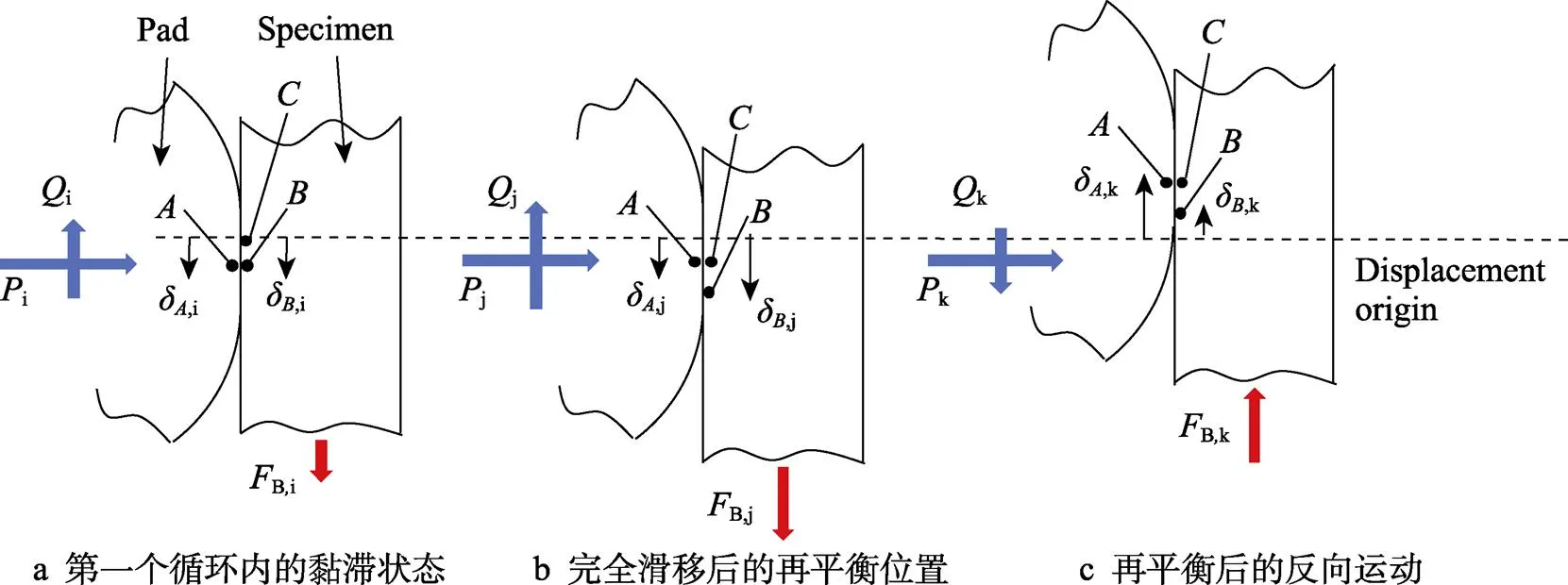
图3 试件与微动垫运动过程示意图

2 微动疲劳有限元仿真分析

2.1 微动问题的接触有限元模型

接触区应力应变场分析是进行微动疲劳损伤研究的重要基础。通过接触分析得到的接触区的应力应变分布是裂纹萌生位置、裂纹初始扩展方向和微动疲劳损伤的主要控制参数[25-26]。

由于多轴加载条件下的微动过程非常复杂，可以建立有限元分析模型来辅助分析这一问题。本文利用有限元软件ABAQUS建立了二维（平面应变）模型（见图4），模拟了微动垫和试件在循环法向载荷和轴向载荷下的接触状态。模型分为3个主要部分：微动垫、试件和横向弹簧。圆柱体的半径为100 mm，微动垫夹具模拟为横向弹簧，通过为微动垫夹具材料定义小的弹性模量，横向弹簧具有低刚度，横向弹簧左边缘节点的所有自由度都是固定的，这限制了微动垫的刚性运动。对于平面试件，左边缘节点的方向自由度和下边缘节点的方向自由度是固定的，以限制试件的刚性运动。然后，在微动垫的上边缘施加法向载荷，在试件的右边缘施加轴向载荷。可变法向载荷和轴向载荷见式（2）。

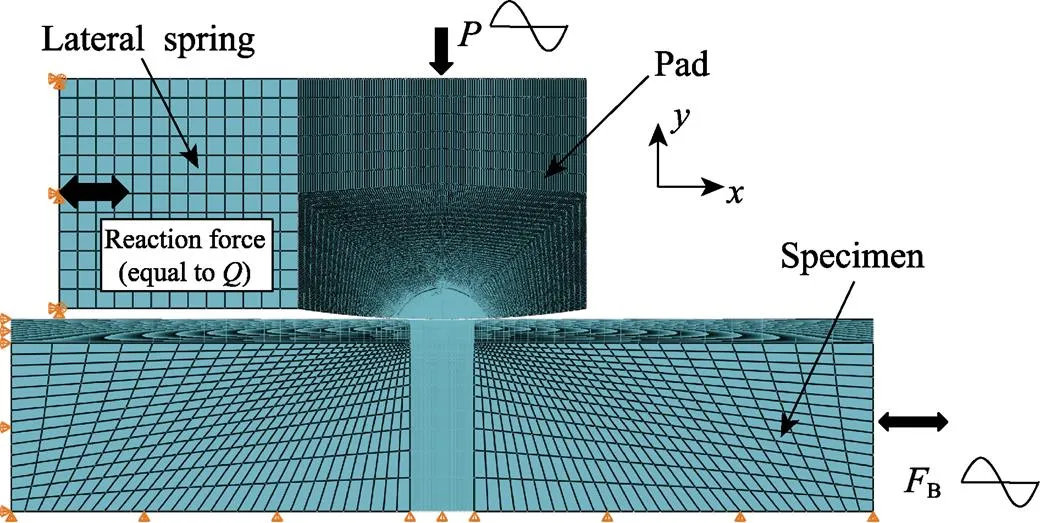
图4 多轴加载有限元分析模型

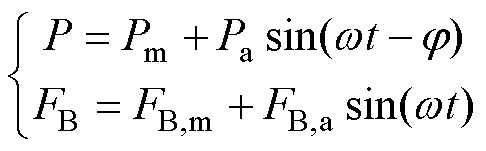
式中：m是法向载荷的均值；a是法向载荷的振幅；B,m是轴向载荷的均值；B,a是轴向载荷的振幅；是法向载荷和轴向载荷之间的相位差。

接触分析为高度非线性问题，接触区有限元网格的质量和单元尺寸直接影响到计算的收敛性和精度。因此对接触区的网格进行了加密，使用尺寸为10 μm× 10 μm的正方形网格可以满足计算要求。将微动垫和试件的对应区域定义为接触，接触行为遵循库仑摩擦定律，定义滑动摩擦因数为=0.65。垫片和试件的材料均为2024-T351铝合金，其弹性模量=74 100 MPa，泊松比=0.33。

2.2 有限元模拟的加载分析过程及参数设置

载荷分三步施加到模型上。第一步，施加一个小的法向载荷来建立微动垫和试件之间的接触；第二步，将法向载荷的均值a应用于模型；第三步，施加循环轴向载荷B和法向载荷来模拟多轴循环荷载工况。利用ABAQUS子程序DLOAD对模型施加动态载荷。由于微动状态在第二个循环中是稳定的，因此模拟了2个加载循环，并将每个循环分为100个子步骤进行详细分析。

该模拟的主要目的是研究可变法向载荷和相位差对接触行为的影响，因此在所有模拟情况下都使用了一个水平的轴向载荷，应力比=‒1，B,a=100 MPa，以及循环法向载荷m=225.2 N/mm，a=77 N/mm（对应从140 MPa到200 MPa的最大接触应力0）。采用3个相位差（=0°、45°、90°）和2个弹簧刚度（f=2 084、3 770 N/mm，分别对应于弹簧的弹性模量模量s= 1 990、3 600 MPa）来评估多轴加载对微动运行状态的影响。

3 有限元结果分析

根据2.2节中的加载设置，进行了一系列有限元仿真模拟，输出横向弹簧左侧边缘的反作用力（如图4所示）等于切向力，以便进一步分析。

3.1 不同载荷条件下的Ft-D曲线特征

t曲线（t是切向力，是相对位移幅值）的轴为，轴为，是分析微动状态最重要的动力学信息[27]。Vingsbo等[28]提出了“微动图”的概念，阐明微动磨损参数与微动磨损之间的关系。Zhou等[29]系统地研究了t曲线与微动损伤之间的关系，提出了微动图理论来解释微动机理。他们提出t曲线具有3种典型的形状（见图5）：（1）线性t曲线，表示接触中心处于黏着状态，接触边缘出现微滑移，对应部分滑移的微动运行状态；（2）椭圆t曲线，表示接触体间的相对运动由弹塑性变形来协调，但微动运行状态仍为部分滑移；（3）平行四边形的t曲线，对应全局滑动的微动运行状态[30]。这3种类型的t曲线基于恒定的法向加载条件。然而，随着法向载荷的变化，t曲线会发生显著变化。

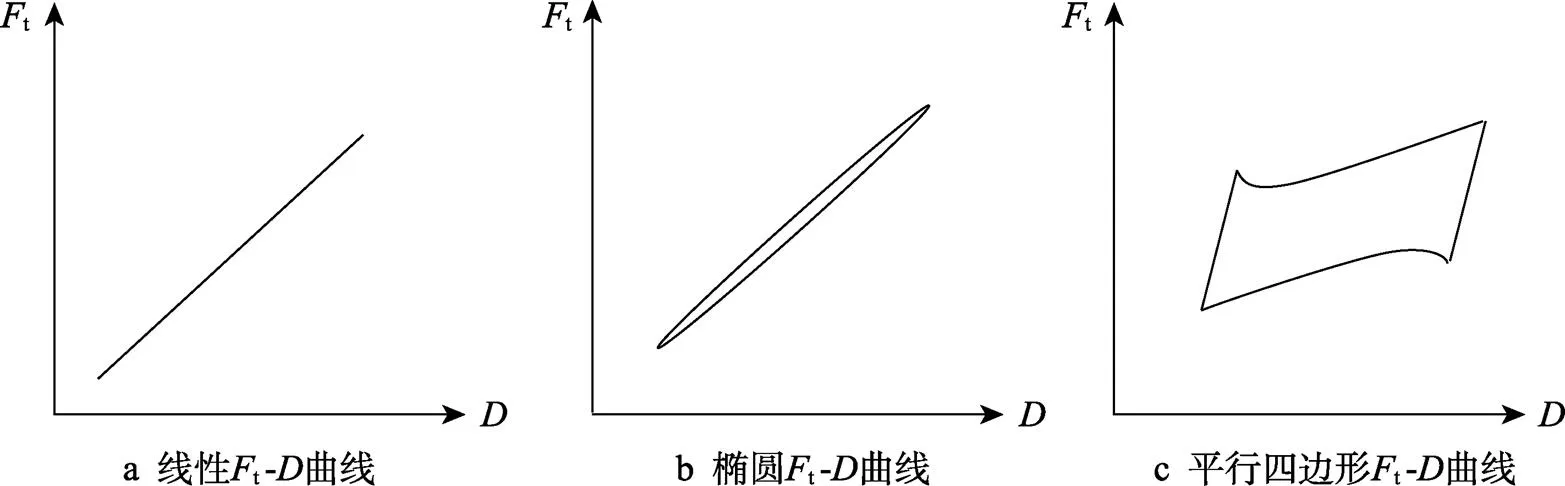
图5 典型的Ft-D曲线

如图6所示，在刚度为2 084 N/mm、相位差为0°时，切向力加载曲线几乎是线性的，运行状态保持为部分滑移状态，与图5a相似。如图7所示，f=3 770 N/mm、=0°时，由于刚度增加，在开局有不稳定的滑移阶段后，曲线稳定为平行四边形，表明此加载下有周期性的完全滑移阶段，与图5c相似。

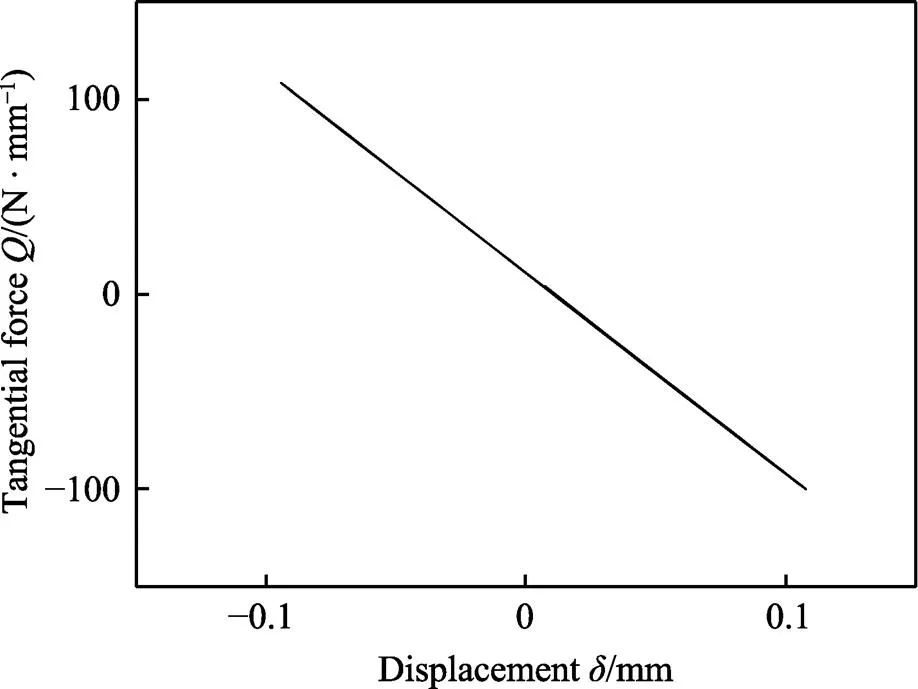
图6 微动垫夹具刚度较小时比例加载条件下的Ft-D曲线（kf =2 084 N/mm，φ= 0°）

f=3 770 N/mm、= 90°加载时，如图8所示，在可变法向载荷和相位差的影响下，曲线两端形状发生了扭曲，近似处于梯形，产生这种状态的原因在于，与恒定的法向载荷且无相位差的加载条件相比，完全滑移阶段的切向力不再保持恒定，所以曲线两端形成了不规则的形状。

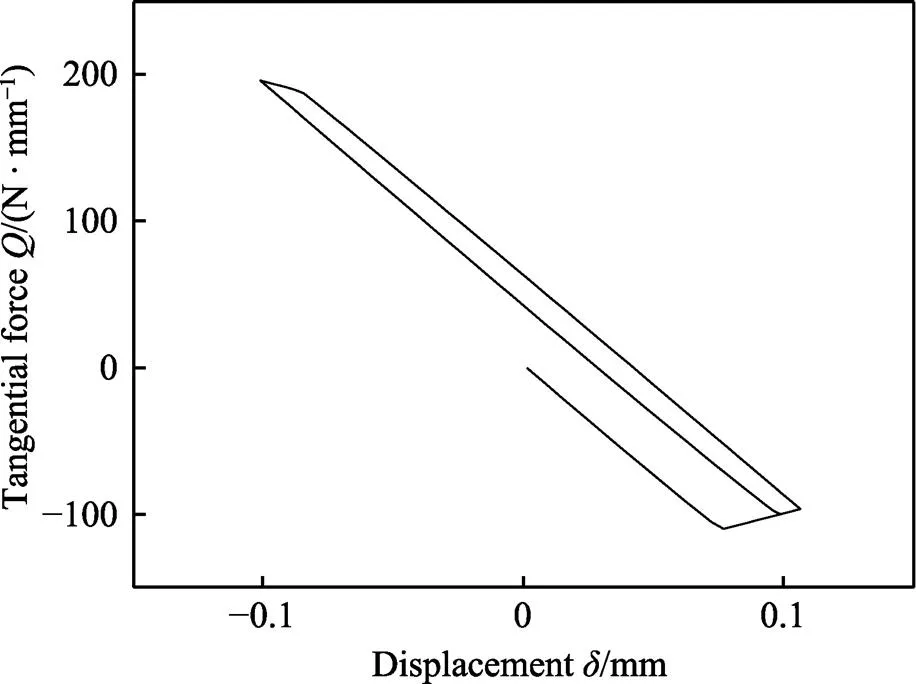
图7 微动垫夹具刚度较大时比例加载条件下的Ft-D曲线（kf=3 770 N/mm，φ= 0°）

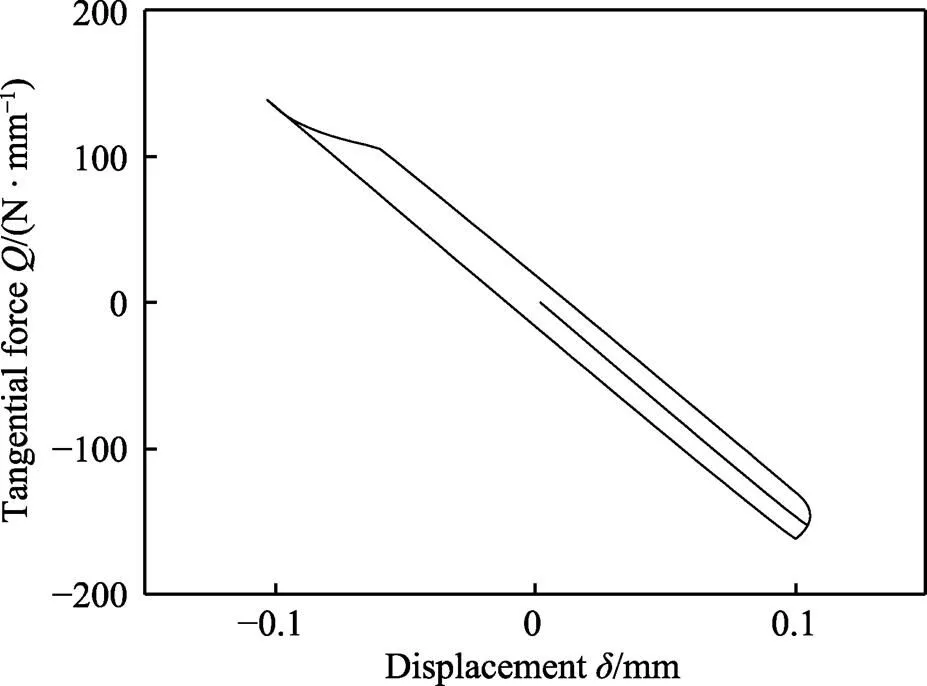
图8 微动垫夹具刚度较大时非比例加载条件下的Ft-D曲线（kf=3 770 N/mm，φ= 90°）

3.2 Q-P曲线分析方法及讨论

由于在加载参数可变的多轴载荷条件下，运行状态非常复杂且难以分析，所以在本节中提出了一种-曲线分析方法来辅助分析这些复杂微动情况下的运行状态特性。

3.2.1曲线分析模型

切向力历程和t-曲线提供的信息对于多轴载荷条件下的微动运行状态分析是有限的。基于阿蒙顿-库仑定律，发现和的函数可以提供更多关于微动运行状态的有用信息。

如果接触状态在加载循环期间保持部分滑移状态，和的函数可设为：

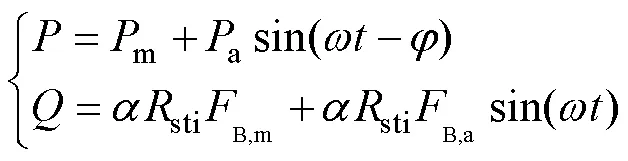
显然，和的关系服从椭圆方程。如果把线性曲线=±和-椭圆曲线放在同一个坐标系中，它们之间有5个典型的条件（见图9）：（1）不相交；（2）在一点相切；（3）在两点相切；（4）在两点相交；（5）在三点相交；（6）在四点相交。椭圆的中心坐标、长轴和短轴的长度以及倾斜角影响线性曲线和椭圆曲线之间的关系。而所有这些因素都是由方程中的加载参数控制的。

在上面的讨论中，没有考虑滑动摩擦力的影响，而实际上，当椭圆曲线越过=±线时，曲线的形状会发生变化，即线性曲线=±是部分滑移与完全滑移的分界线。在实际情况下，椭圆和曲线的交叉部分不具有物理意义，这些部分的载荷路径（图9d—f中的虚线部分）会变成与线性曲线=±重合的线性曲线。因此，图9a—c为部分滑移区，图9d—f有稳定的完全滑移区。

3.2.2 比例加载条件下的微动运行状态

在比例加载条件下，-椭圆函数可以化为线性函数，定义载荷幅值比为amp=B,a/a，则函数进一步可化为：

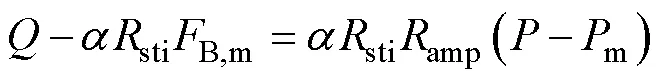
从公式（5）可以看出，线性曲线有一个中心坐标(m,stiB,m)，斜率为stiamp，即m决定曲线的水平位置，sti、B,m和决定曲线的垂直位置，曲线的旋转角度由sti、amp和决定。

如图10所示，2种刚度曲线均为线性函数，并且随着弹簧刚度增加，曲线的斜率增加，小刚度曲线完全包含在内，则其完全为部分滑移，而大刚度的曲线与两条边都有相交，说明其运行状态有完全滑移。

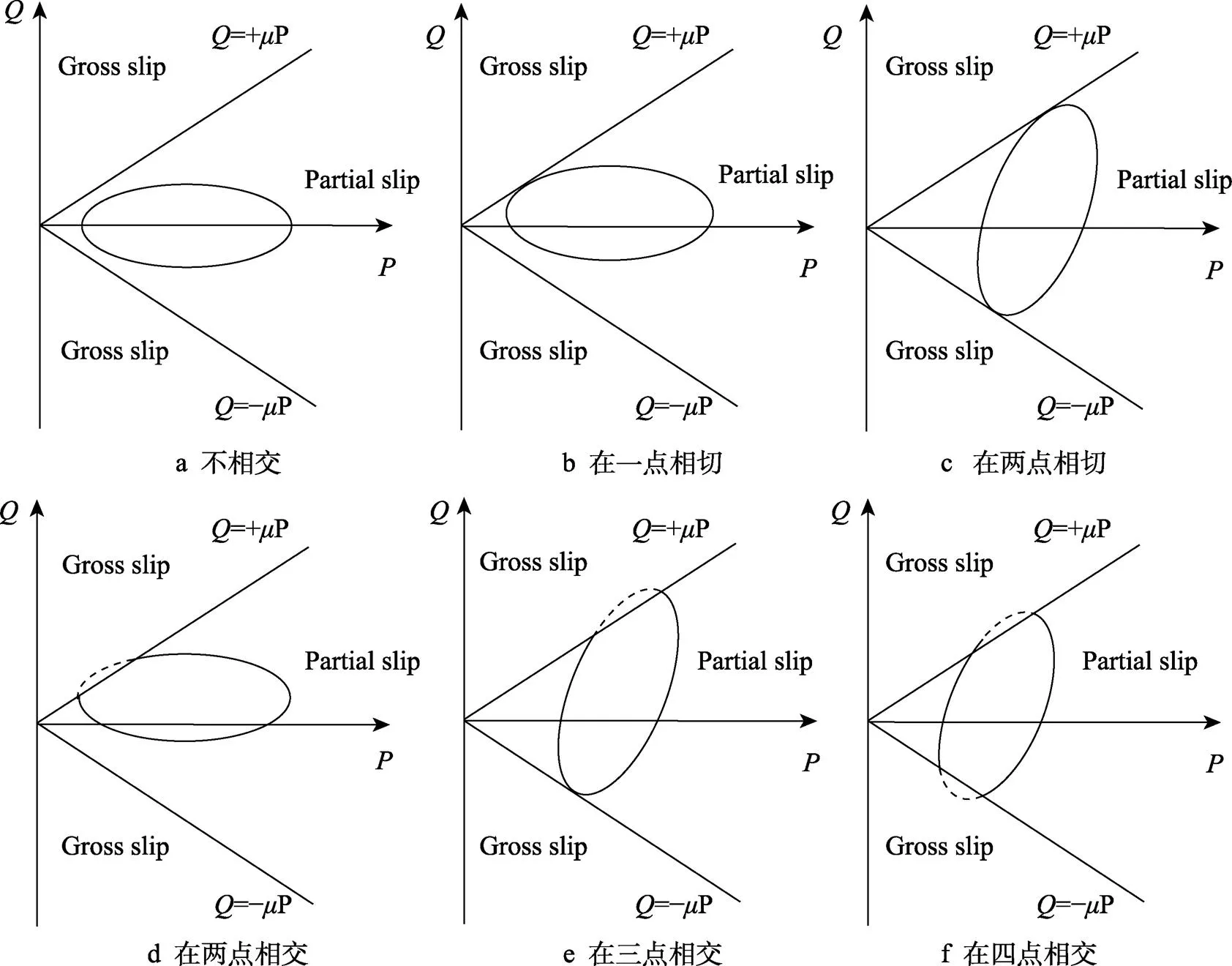
图9 直线Q=±μP和Q-P椭圆曲线之间的可能位置

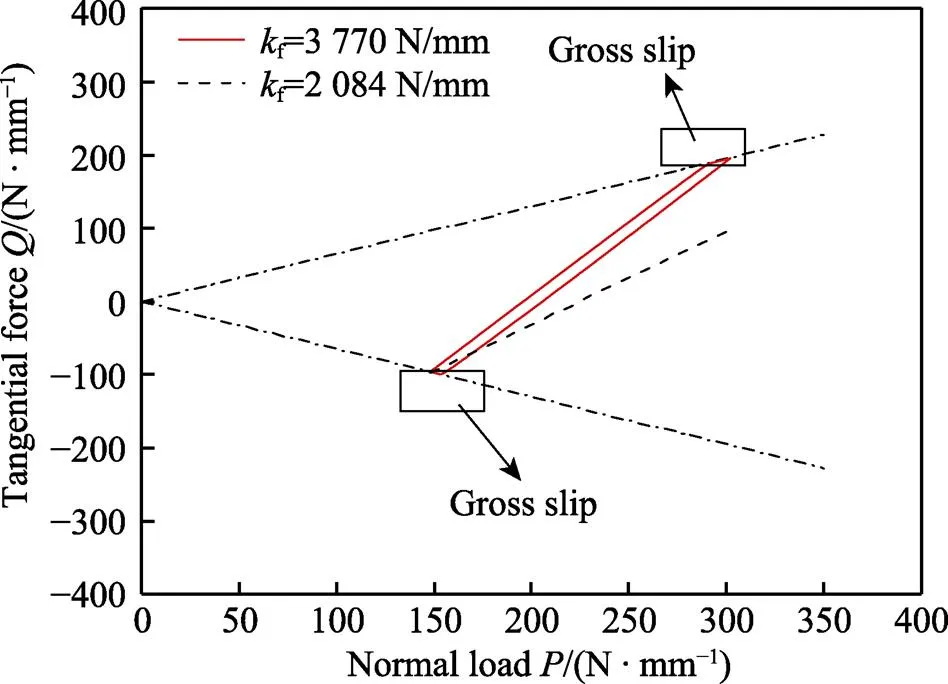
图10 相位差φ=0°多轴加载条件下的Q-P曲线

3.2.3 非比例加载条件下的微动运行状态

在非比例加载条件下，椭圆轴与坐标系不平行，函数曲线会变得复杂。有相位差时，根据式（5），曲线可化为标准椭圆函数：

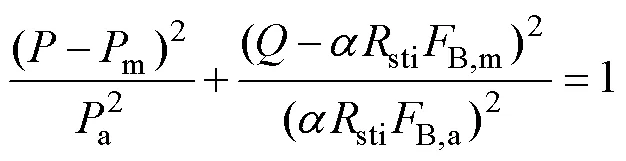
椭圆方程的中心坐标为(m,stiB,m)，长轴由a决定，短轴由sti、B,a和决定。相位差为45°时，如图11所示，大刚度曲线的短轴和长轴都比小刚度的大，且有一定的旋转，小刚度椭圆始终保持在内部，大刚度时椭圆发生逆时针旋转以及短轴和长轴增加导致与=±相交于四点，形成稳定的完全滑移阶段。

图11 相位差=45°多轴加载条件下的曲线

Fig.11 The-curve under multi-axial loading condition with phase difference=45°

如图12所示，在加载相位为90°时，可以看出当弹簧刚度增加时，椭圆的长轴和中心点几乎保持不变，但是短轴明显增加，所以能得到在此相位时刚度增加的影响主要在于使短轴增加，导致大刚度椭圆与=±上下两边都有相交，发生了完全滑移。

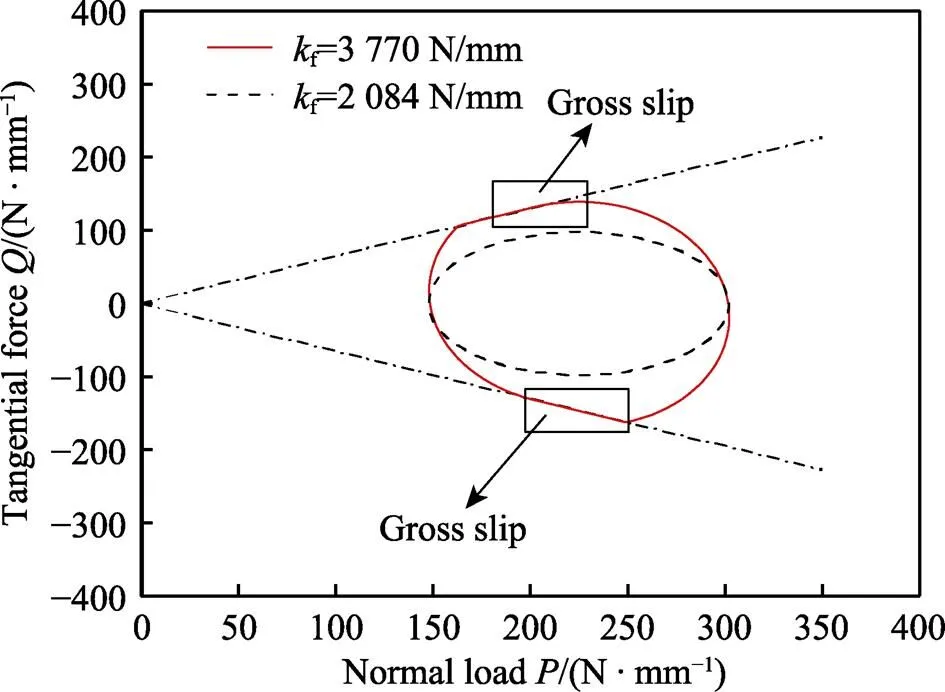
图12 相位差φ=90°多轴加载条件下的Q-P曲线

4 试验验证

在PWS-25G疲劳试验机上进行了一系列试验，以评估曲线分析方法的合理性。采用加载条件（B,a=10 kN，B,m=0 kN，a=1.54 kN，m=‒4.5 kN，=0°、45°、90°）进行微动疲劳试验。相位差为0°时，图13a、图14a所示，接触区只存在少量的表面塑性变形。相位差为45°时，图13b接触区域均覆盖黑色的氧化层，并且从图14b中可以看出接触区存在大量的塑性划痕及变形。相位差为90°时，如图13c所示，接触区域氧化层较图13b显著增加，图14c中可以看出磨损的程度很深，范围大。

图13 不同相位差微动疲劳试验磨损状态

图14 磨损表面的三维形貌

结合图15所示的-图，可对上述微动状态进行进一步的讨论。=0°的加载条件下，-曲线近似直线，=45°时曲线近似为椭圆，处在=±曲线内部。值得注意的是，其与= ‒近似相切。=90°时，直线部分与=±曲线平行，其余部分近似为椭圆曲线。根据本文提出的分析方法可推断，在相位差为0°和45°时，接触状态为部分滑移，相位差为90°时，接触状态为完全滑移。反映到图13、图14所示的微动接触区形态上，可判断图13a所示的微动处在部分滑移状态；图13c所示的微动处在完全滑移状态。图13b较为特殊，从接触区形貌分析，可见其既有塑性变形又有较多的氧化层（但较图13c少）。结合-图推测，因其-曲线与=‒近似相交，在微动运行的有限局部（切点附近）接触状态会短时为完全滑移，进而产生了较多的磨屑，但总体上该状态仍为部分滑移。

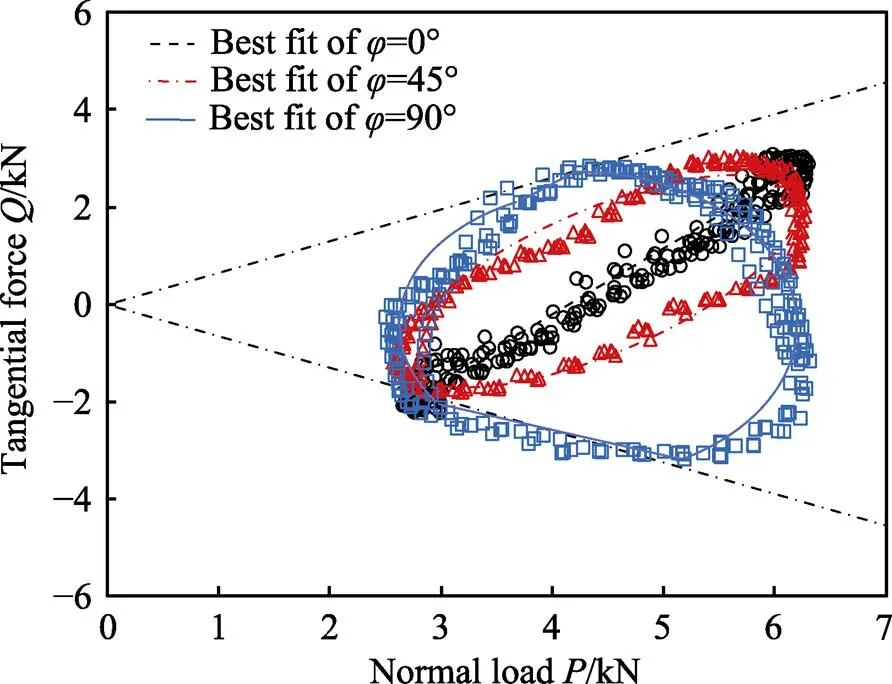
图15 不同相位差下微动疲劳试验的Q-P曲线

5 结论

1）对于部分滑移状态，微动垫和试件保持静摩擦状态，微动垫的位移与试样同步，由于切向力是由微动垫夹具（“弹簧”）的变形产生的，因此它与相位差和法向载荷的变化无关，仅取决于轴向载荷。

2）对于完全滑移状态，t曲线不是规则的平行四边形，这是由于法向荷载以及相位差的变化，导致曲线变得极其复杂。反映到曲线上，表现为椭圆与=±相交，产生了完全滑移。曲线变为由部分椭圆曲线与直线=±组合成的类椭圆曲线。由此可详细地了解加载循环中不同时期的微动运行状态。

3）在比例加载条件下，曲线为直线函数。曲线的水平位置与m呈正相关，垂直位置与sti、B,m和呈正相关，曲线的旋转角度与sti、amp和呈正相关。

4）在非比例加载条件下，曲线是椭圆函数。m、sti、B,m和影响椭圆的中心坐标，而a、sti、B,a和影响长轴和短轴的长度，影响椭圆的斜率。

[1] 杨茂胜, 陈跃良, 郁大照, 等. 微动疲劳研究的现状与展望[J]. 强度与环境, 2008, 35(6): 45-54.

YANG Mao-sheng, CHEN Yue-liang, YU Da-zhao, et al. Several Key Problems in Studying on Fretting Fatigue[J]. Structure & Environment Engineering, 2008, 35(6): 45-54.

[2] 刘道新, 何家文. 微动疲劳影响因素及钛合金微动疲劳行为[J]. 航空学报, 2001, 22(5): 454-457.

LIU Dao-xin, HE Jia-wen. Review of Factors that Influence Fretting Fatigue (FF) and Investigation on Ff Behavior of Ti-Alloy[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(5): 454-457.

[3] ARAÚJO J A, NOWELL D. The Effect of Rapidly Varying Contact Stress Fields on Fretting Fatigue[J]. International Journal of Fatigue, 2002, 24(7): 763-775.

[4] ARAÚJO J A, CASTRO F C, MATOS I M, et al. Life Prediction in Multiaxial High Cycle Fretting Fatigue[J]. International Journal of Fatigue, 2020, 134: 105504.

[5] WATERHOUSE R B. Fretting fatigue[M]. London: Applied Science Publishers, 1981

[6] 何明鉴. 机械构件的微动疲劳[M]. 北京: 国防工业出版社, 1994.

HE Ming-jian. Fretting Fatigue of Mechanical Comp­onents[M]. Beijing: National Defense Industry Press, 1994.

[7] NOWELL D, DINI D, HILLS D A. Recent Developments in the Understanding of Fretting Fatigue[J]. Engineering Fracture Mechanics, 2006, 73(2): 207-222.

[8] RUIZ C, BODDINGTON P B, CHEN K C. An Invest­igation of Fatigue and Fretting in a Dovetail Joint[J]. Experimental Mechanics, 1984, 24(3): 208-217.

[9] HOEPPNER D, ADIBNAZARI S, MOESSER M W. Literature Review and Preliminary Studies of Fretting and Fretting Fatigue Including Special Applications to Aircraft Joints[J]. Fracture Mechanics, 1994

[10] 古远兴. 高低周复合载荷下燕尾榫结构微动疲劳寿命研究[D]. 南京: 南京航空航天大学, 2007.

GU Yuan-xing. Research on Fretting Fatigue Life of Dovetail Joint under HCF-LCF Load[D]. Nanjing: Nan­jing University of Aeronautics and Astronautics, 2007.

[11] 徐友良, 崔海涛, 陈伟. 基于临界面法的燕尾榫连接结构微动疲劳寿命预测[J]. 航空动力学报, 2013, 28(3): 489-493.

XU You-liang, CUI Hai-tao, CHEN Wei. Fretting Fatigue Life Prediction Based on Critical Plane Approach for Dovetail Joint[J]. Journal of Aerospace Power, 2013, 28(3): 489-493.

[12] 米雪, 唐攀, 沈平川, 等. 690合金管在不同法向载荷下的切向微动磨损性能研究[J]. 表面技术, 2020, 49(11): 191-197.

MI Xue, TANG Pan, SHEN Ping-chuan, et al. Tangential Fretting Wear Characteristics of 690 Alloy Tubes under Different Normal Force[J]. Surface Technology, 2020, 49(11): 191-197.

[13] 景鹏飞, 俞树荣, 宋伟, 等. 接触载荷对TC4钛合金微动磨损行为的影响[J]. 表面技术, 2019, 48(11): 266-274.

JING Peng-fei, YU Shu-rong, SONG Wei, et al. Effect of Contact Load on Fretting Wear Behavior of TC4 Titanium Alloy[J]. Surface Technology, 2019, 48(11): 266-274.

[14] 石炜, 温卫东, 崔海涛. 轴向和法向应力对DD3和DZ125镍基合金微动疲劳性能的影响[J]. 机械工程材料, 2014, 38(11): 10-15.

SHI Wei, WEN Wei-dong, CUI Hai-tao. Effects of Axial and Normal Stresses on Fretting Fatigue Properties of DD3 and DZ125 Nickel-Based Alloys[J]. Materials for Mechanical Engineering, 2014, 38(11): 10-15.

[15] VAN PETEGHEM B, FOUVRY S, PETIT J. Effect of Variable Normal Force and Frequency on Fretting Wear Response of Ti-6Al-4V Contact[J]. Wear, 2011, 271(9-10): 1535-1542.

[16] FOUVRY S, ARNAUD P, MIGNOT A, et al. Contact Size, Frequency and Cyclic Normal Force Effects on Ti-6Al-4V Fretting Wear Processes: An Approach Combining Friction Power and Contact Oxygenation[J]. Tribology International, 2017, 113: 460-473.

[17] ABBASI F, MAJZOOBI G H. Effect of Contact Pressure on Fretting Fatigue Behavior under Cyclic Contact Loading[J]. Surface Review and Letters, 2017, 24(Supp02): 1850032.

[18] ABBASI F, MAJZOOBI G H. Effect of Out-of-Phase Loading on Fretting Fatigue Response of Al7075-T6 under Cyclic Normal Loading Using a New Testing Apparatus[J]. Engineering Fracture Mechanics, 2018, 188: 93-111.

[19] LIAO Jia-peng, TAN Ji-bo, WU Xin-qiang, et al. Effects of Normal Load on Fretting Corrosion Fatigue of Alloy 690 in 285 ℃ Pure Water[J]. Corrosion Science, 2018, 141: 158-167.

[20] SUN Shou-yi, LI Lei, HE Kun, et al. Fretting Fatigue Damage Mechanism of Nickel-Based Single Crystal Superalloys at High Temperature[J]. International Journal of Mechanical Sciences, 2020, 186: 105894.

[21] CIAVARELLA M, DEMELIO G. A Review of Analytical Aspects of Fretting Fatigue, with Extension to Damage Parameters, and Application to Dovetail Joints[J]. International Journal of Solids and Structures, 2001, 38(10-13): 1791-1811.

[22] RAJASEKARAN R, NOWELL D. Fretting Fatigue in Dovetail Blade Roots: Experiment and Analysis[J]. Tribo­logy International, 2006, 39(10): 1277-1285.

[23] BARBER J R, DAVIES M, HILLS D A. Frictional Elastic Contact with Periodic Loading[J]. International Journal of Solids and Structures, 2011, 48(13): 2041- 2047.

[24] HOJJATI-TALEMI R, WAHAB M A, DE BAETS P. Finite Element Simulation of Phase Difference Effects on Fretting Fatigue Crack Nucleation Behaviour[J]. Procee­dings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2014, 228(4): 470-479.

[25] 赵华, 金雪岩, 朱民昊, 等. 微动接触应力的数值分析[J]. 四川大学学报(工程科学版), 2003, 35(5): 32-36.

ZHAO Hua, JIN Xue-yan, ZHU Min-hao, et al. Nume­rical Analysis of Fretting Contact Stresses[J]. Journal of Sichuan University (Engineering Science Edition), 2003, 35(5): 32-36.

[26] 赵华, 周仲荣. 数值方法在微动疲劳研究中的应用进展[J]. 摩擦学学报, 2000, 20(4): 317-320.

ZHAO Hua, ZHOU Zhong-rong. Application and Progress of Numerical Methods in Analysis of Fretting Fatigue[J]. Tribology, 2000, 20(4): 317-320.

[27] 周仲荣, Leo Vincent. 微动磨损[M]. 北京: 科学出版社, 2002.

ZHOU Zhong-rong. Fretting wear[M]. Beijing: Science Press, 2002.

[28] VINGSBO O, SÖDERBERG S. On Fretting Maps[J]. Wear, 1988, 126(2): 131-147.

[29] ZHOU Z R, VINCENT L. Cracking Induced by Fretting of Aluminium Alloys[J]. Journal of Tribology, 1997, 119(1): 36-42.

[30] ZHOU Z R, VINCENT L. Mixed Fretting Regime[J]. Wear, 1995, 181-183: 531-536.

Fretting Running State under Complex Alternating Loads

(School of Mechanical-electronic and Vehicle Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China)

The present common-used fretting fatigue models simplify the actual loading conditions of engineering cases and ignore the effect of variable normal load. In this paper, the contact behavior of the fretting fatigue model subjected to variable normal load and axial load was investigated. The running state of fretting under alternating load was studied. Acurve analysis method was proposed. The contact state under typical loading conditions was discussed, and the influence of different loading parameters on the fretting running state was revealed. It shows that the proposedcurves analysis method can provide guidance for the study of the fretting running state under actual engineering working conditions.

A two-dimensional (plane strain) model was established by using the finite element software ABAQUS to simulate the contact state of the fretting pad and the specimen under cyclic normal load and axial load. The model was divided into 3 main parts: the fretting pad, the specimen and the transverse spring. The normal load was applied to the upper edge of the fretting pad and the axial load was applied to the right edge of the specimen. The main purpose of this simulation was to study the effect of variable normal load and phase difference on the contact behavior, so a bulk axial load with stress ratio= ‒1,B,a=100 MPa and cyclic normal loadm=225.2 N/mm anda=77 N/mm (which corresponds to maximum contact stress0from 140 MPa to 200 MPa). Three phase difference=0°, 45°, 90° and two spring stiffnessf=2 084 N/mm, 3 770 N/mm (corresponding to the Young’s modulus of the springs= 1 990 MPa, 3 600 MPa, respectively) were used to evaluate the effect of multi-axial loading on the micro-action fatigue operating condition, with the reaction force at the left edge of the output transverse spring equal to the tangential force.

A series of fretting fatigue test corresponding to the simulation was performed on a biaxial fretting fatigue testing system The biaxial fretting fatigue testing system has two hydraulic actuators and three load cells, through which the loading of variable normal loads, bulk loadBand the measurement of tangential forcescould be implemented. A series of tests were performed using loading conditions (B,a=10 kN;B,m=0 kN;a=1.54 kN;m= ‒4.5 kN;=0°, 45°, 90°) and the loading loops with different phase differences were recorded to evaluate the rationality of thecurve analysis method.

For proportional loading conditions, thetcurve is a straight line for a small pad fixture stiffness, the curve changes to a regular parallelogram for a larger stiffness. In these conditions, thecurves are linear functions, and the slope of the curve increases as the increase of spring stiffness.

For non-proportional loading conditions, the shape of thetcurve is no longer a parallelogram and becomes very peculiar. Thecurves obey the ellipse function. The shape of the ellipse is determined by pad fixture stiffness, normal and bulk loading parameters, the phase difference etc.

The proposedcurves analysis method can provide a guidance for the study of the fretting fatigue running state, and also provides a method for further discussion of fretting fatigue or fretting wear behavior.

fretting; complex alternating load; dynamics; contact state; finite element simulation

O346.2

A

1001-3660(2023)01-0112-09

10.16490/j.cnki.issn.1001-3660.2023.01.012

2021–12–28；

2022–04–08

2021-12-28；

2022-04-08

国家自然科学基金青年基金项目（51905028）；北京市教育委员会科技计划一般项目（KM202110016002）；北京建筑大学金字塔人才培养工程（JDYC20200323）

National Natural Science Foundation of China Youth Fund Project (51905028); Beijing Municipal Education Commission Science and Technology Plan General Project (KM202110016002); Beijing University of Civil Engineering and Architecture Pyramid Talent Training Project (JDYC20200323)

田帅（1996—），男，硕士生，主要研究方向微动疲劳损伤机理

TIAN Shuai (1996-), Male, Postgraduate, Research focus: fretting fatigue damage regime

李欣（1984—），男，博士，副教授，主要研究方向为机械结构强度及疲劳耐久性分析

LI Xin (1984-), Male, Doctor, Associate professor, Research focus: mechanical structure strength and fatigue durability analysis

田帅, 李欣, 杨建伟, 等.复杂交变载荷条件下微动运行状态[J]. 表面技术, 2023, 52(1): 112-120.

TIAN Shuai, LI Xin, YANG Jian-wei, et al. Fretting Running State under Complex Alternating Loads[J]. Surface Technology, 2023, 52(1): 112-120.

责任编辑：万长清