考虑过采样器与分类器参数优化的变压器故障诊断策略

栗 磊，王廷涛，赫嘉楠，牛 健，梁亚波，苗世洪

（1. 国网宁夏电力有限公司电力科学研究院，宁夏银川 750002；2. 华中科技大学电气与电子工程学院，湖北武汉 430074）

0 引言

电力变压器作为连接不同电压等级的关键设备，在电力系统的输、变、配电过程中起到不可替代的作用。因此，准确掌握变压器的健康状态，尤其是当变压器出现异常或故障后的及时诊断，对于保障电力系统的安全稳定运行具有重要意义。

电力变压器按绝缘介质可分为油浸式变压器、干式变压器和SF6气体绝缘变压器，其中以油浸式变压器居多。针对油浸式变压器的故障，传统方法主要通过分析变压器油中溶解气体含量的比值特征进行诊断，其代表为IEC 三比值法［1］、立体图示法［1-2］、大卫三角形法［3-4］等。此类方法简便实用，但存在准确率较低、判据过于绝对等问题。近年来，基于人工智能算法的变压器故障诊断技术逐步发展起来。此类方法通常以变压器油中溶解气体含量等作为指标，通过大量历史故障样本来训练神经网络［5-6］、极限学习机［7-8］、相关向量机［9-10］、支持向量机（support vector machine，SVM）［11-12］等人工智能模型，使其具有识别变压器故障类型的能力。与传统方法相比，人工智能方法在诊断准确率方面有较大提升。然而，变压器故障样本通常具有类间样本数量不平衡的问题［13］，当采用人工智能方法对不平衡故障样本进行分类时，分类结果容易偏向多数类样本。

为提高人工智能方法对不平衡样本的分类性能，可以对样本进行均衡化处理，主要有欠采样和过采样2 种思路。前者是通过删除部分多数类样本实现类间样本平衡，后者则是通过生成少数类样本实现。由于欠采样可能会丢失原样本集的有效信息，导致分类不准确［14］，因此目前相关研究大多采用过采样。过采样算法中应用最为广泛的是合成少数过采样技术（synthetic minority oversampling technique，SMOTE）［15-18］算法及其改进算法，如自适应综合过采样（adaptive synthetic sampling，ADASYN）［12，14］、SVM SMOTE［13］、基于围绕中心点的划分聚类的SMOTE［19］算法等。上述算法的应用使得变压器故障诊断的准确率进一步提升，但仍有可改进之处，具体有如下2个方面。

1）SMOTE 算法存在一定的缺陷。首先，SMOTE算法依靠少数类样本集生成新样本，若所选样本为噪声样本，则生成样本同样属于噪声，扰乱样本集的正确分类。其次，SMOTE 算法生成新样本时不考虑多数类样本的分布情况，容易加重多数类与少数类的边界重叠问题，使得类边界更加模糊。此外，SMOTE 算法生成新样本时不考虑少数类样本的分布情况，若少数类样本内部分布不均匀，则经SMOTE 算法过采样后不均匀程度会进一步加剧，使得少数类内部稀疏区样本不易识别。虽然现有改进算法对前两点缺陷进行了一定的改善［20］，但鲜有算法针对第三点缺陷提出改进措施。

2）过采样倍率优化问题。过采样倍率用于衡量生成新样本的数量，若不对少数类样本进行过采样，则倍率为0，若采用过采样使少数类、多数类样本数量一致，则倍率为1。倍率越小，对原样本集改动越小，但不利于强化少数类样本的数据特征；倍率越大，少数类样本的数据特征越强，但易引入噪声。因此过采样倍率选择是一个参数优化问题［21］，而目前在变压器故障诊断领域鲜有研究考虑这一问题。

针对上述问题，本文提出一种考虑过采样器与分类器参数优化的变压器故障诊断策略。首先，针对SMOTE 方法存在的缺陷，提出其改进方法——基于近邻分布特性的改进SMOTE（SMOTE based on nearest neighbor distribution，SMOTE-NND）算法，采用改进方法对变压器不平衡故障样本进行过采样；其次，选取SVM 作为变压器故障诊断基准分类器，采用层次式有向无环图支持向量机（hierarchical directed acyclic graph SVM，HDAG-SVM）算法搭建变压器故障诊断的多标签分类结构；进而，提出基于层次搜索-改进哈里斯鹰（hierarchical searchmodified harris hawks optimization，HS-MHHO）算法的双层参数优化方法，对过采样倍率、SVM参数进行寻优，以得到泛化能力更强的诊断模型；最后，开展算例分析，验证本文所提方法的有效性。

1 考虑过采样器与分类器参数优化的变压器故障诊断模型结构

1.1 变压器故障类型及特征量

根据标准DL／T 722—2014《变压器油中溶解气体分析和判断导则》［1］，油浸式变压器的故障类型主要有过热故障与放电故障2 类，故障代码分别为T、D。过热故障可细分为低温过热、中温过热、高温过热，故障代码依次为T1、T2、T3；放电故障可细分为局部放电、低能放电、高能放电，故障代码依次为PD、D1、D2。故障样本的特征量主要有氢气（H2）、甲烷（CH4）、乙烷（C2H6）、乙烯（C2H4）、乙炔（C2H2）这5种气体的含量。本文参考该标准给出的故障类型与特征量开展变压器故障诊断研究。

1.2 变压器故障诊断模型结构

变压器故障诊断是一个六分类问题，本文将其分解为7 个二分类问题，先构建7 个不同的SVM 二分类器，再采用HDAG-SVM 算法对上述二分类器进行组合以实现故障诊断的六分类功能。本文变压器故障诊断策略分为数据预处理阶段、诊断模型训练阶段和诊断模型测试阶段，具体结构见附录A图A1。

数据预处理阶段主要包括训练样本分组、样本数据归一化和过采样3个部分，其中归一化公式为：

为使各组训练样本集内多数类样本与少数类样本的数量均衡化，需要对其中的少数类样本进行过采样。过采样后少数类的新增样本数如式（2）所示。

训练阶段，需要对过采样倍率β及SVM 参数进行优化。β决定过采样新增样本的数量，如果β过小则难以突出少数类样本的数据特征，如果β过大则容易引入噪声，因此需要对β的取值进行寻优。同样地，SVM的分类性能受其参数的影响，本文选用高斯核函数作为SVM 的核函数，则待优化SVM 参数为误差惩罚参数C和高斯核宽度σ［11］。

测试阶段，将未知类别故障样本集送入已训练好的变压器故障诊断多标签分类器进行诊断，可得到故障样本的诊断结果集。

2 基于SMOTE-NND 算法的变压器故障样本均衡化方法（过采样器）

由于变压器故障样本存在类间不平衡问题，需要对少数类样本进行过采样，其中最常用的方法为SMOTE 方法，该方法通过线性插值的方式在2 个少数类样本间生成新样本，其原理可参考文献［16］。鉴于传统SMOTE 算法存在模糊类边界、易产生噪声、少数类内部不均匀等问题，本文提出一种SMOTE-NND算法，该方法综合考虑少数类样本近邻内各类样本的数量及欧氏距离，并据此分配每个少数类样本生成过采样样本的数量，方法流程图如图1所示。

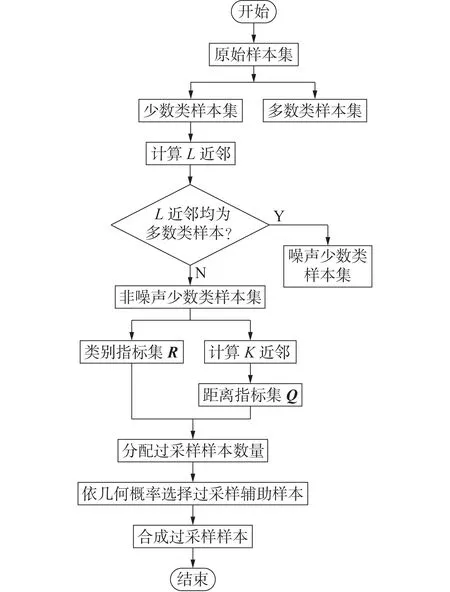
图1 SMOTE-NND算法流程图Fig.1 Flowchart of SMOTE-NND algorithm

SMOTE-NND算法的关键步骤如下。

1）计算每个少数类样本在原始样本集范围内的L近邻，将L近邻内均为多数类样本的少数类样本认定为噪声。

2）计算非噪声少数类样本的类别指标，L近邻内多数类样本越多，则类别指标越大，如式（3）所示。

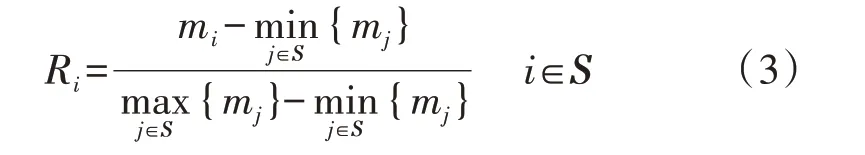
式中：S为非噪声少数类样本集；Ri为样本i的类别指标；mi为样本i的L近邻内多数类样本的数量。

3）计算非噪声少数类样本在自身样本集范围内的K近邻，并计算距离指标，K近邻欧氏距离平均值越大，则距离指标越大，如式（4）所示。

式中：Qi为样本i的距离指标；Di为样本i与其K近邻欧氏距离的平均值。

4）依据类别指标和距离指标为非噪声少数类样本分配过采样样本数量，如式（5）所示。

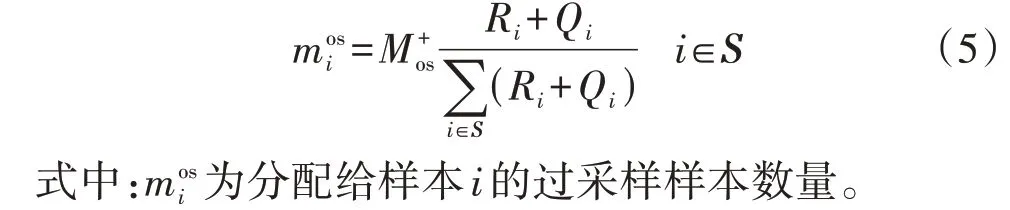
5）将非噪声少数类样本作为过采样根样本，在K近邻内依据各近邻样本到根样本欧氏距离的几何概率随机选择过采样辅助样本。

6）将过采样根样本和辅助样本分别记为xroot、xaux，则过采样生成的样本xos如式（6）所示。

式中：r为［0，1］范围内的随机数。

由步骤1）可知，SMOTE-NND 算法将L近邻内均为多数类样本的少数类样本认定为噪声，不对其进行过采样，可尽量避免引入新的噪声。由步骤2）、4）可知，SMOTE-NND 算法使L近邻内多数类样本较多的非噪声少数类样本生成更多的过采样样本，从而避免类边界少数类样本被淹没，起到强化类边界的作用。由步骤3）—5）可知，SMOTE-NND 算法使K近邻欧氏距离平均值较大的非噪声少数类样本生成更多的过采样样本，并且使K近邻内距离根样本更远的样本被选为辅助样本的概率更大，从而降低少数类样本内部分布的不均匀程度，提高分类器对少数类样本稀疏区的识别率。

3 基于HDAG-SVM 算法的变压器故障样本多分类方法（分类器）

由于变压器属于高可靠性设备，其故障样本数量较少，因此变压器故障诊断问题属于多标签小样本分类问题。作为一种基于结构风险最小化原理的分类模型，SVM 具有训练效率高、泛化能力强、不易陷入局部最优的优点，因此适用于解决变压器故障诊断问题［11，15］。由于SVM 是一种二分类模型，因此处理多标签分类问题时需要采取一定的SVM 组合策略。本文采用HDAG-SVM 算法对变压器故障样本进行分类，具体结构如附录A 图A2 所示。由图A1、A2 可知，HDAG-SVM 算法将训练所得的7 个SVM二分类器组合为层次式有向无环图形式。在诊断阶段，对于任意未知类别的故障样本，HDAG-SVM算法仅需调用3 个SVM 二分类器即可给出诊断结果，且不存在分类重叠、不可分类等问题。

4 基于HS-MHHO 算法的过采样器与分类器参数双层优化方法（参数优化器）

训练阶段，需要对过采样倍率β、SVM 误差惩罚参数C、高斯核宽度σ这3种参数进行优化。本文采用双层优化方法求取参数最优解，上层采用层次搜索（hierarchical search，HS）算法对β寻优，下层采用改进哈里斯鹰算法（modified Harris hawks optimization，MHHO）对SVM参数C和σ寻优。

4.1 基于HS算法的过采样倍率优化方法

HS 算法是对传统遍历搜索的改进，遵循“从整体到局部”的原则，首先采用大步距在整体范围内初步搜索，确定适应度最高的点，进而在以该点为中心的区间内小步距精细化搜索，最终求得全局最优解。采用HS优化β的具体步骤如下。

1）设置整体搜索的范围为［0，1］，步距为Δβw，搜索点为βwt=tΔβw，其中t=0，1，2，…，1/Δβw，1/Δβw为整数。在每个过采样倍率下进行过采样，将利用过采样补充后的扩充训练样本集送入下层MHHO优化模块对SVM 参数进行优化。优化完成后将下层适应度返回至上层HS优化模块。

4.2 基于MHHO算法的SVM参数优化方法

4.2.1 MHHO算法

在上层优化β的过程中，需要将扩充训练样本集送入下层并对SVM 进行参数优化。本文采用MHHO算法优化SVM的误差惩罚参数C和高斯核宽度σ，该算法是在哈里斯鹰（Harris hawks optimization，HHO）算法的基础上改进而来。HHO 算法是一种新型群体智能算法，其通过模拟哈里斯鹰的群体捕猎行为，并结合Lévy 飞行来实现对高维、非连续、不可微等复杂问题的求解，具体算法实现详见文献［22］。

HHO 算法搜索范围较大，搜索效率较高，且针对多极值问题的收敛性能较好，但仍存在一定的缺陷，主要体现在两方面。一是参数设置过于简单，HHO算法中控制迭代进程的2个重要参数分别为猎物逃逸能量E和猎物跳跃强度J，其中E设置为简单的线性衰减，在迭代后期只进行局部开发，易陷入局部最优；而J设置为随机数，忽略了其与E之间的关系。二是位置更新时仅依赖种群个体信息，当种群陷入局部最优后无法产生新位置，使得迭代停滞，算法收敛早熟。针对上述问题，本文提出一系列改进措施，具体如下。

1）改进猎物迭代参数。

将E和J的更新公式改进为：

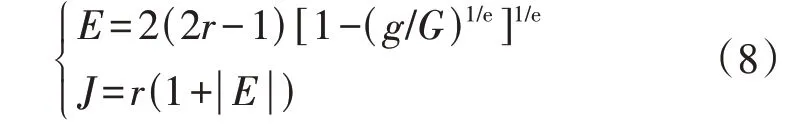
式中：g为当前迭代次数；G为迭代次数上限。改进后E的最值在迭代中后期变化较为平缓，在进行局部开发的同时保留了进行全局探索的可能性，降低了陷入局部最优的风险。改进后J的最值由当前的E值决定，一方面有助于扩大局部开发阶段前期的搜索范围，另一方面有助于提高局部开发阶段后期的搜索精度。

2）logistic混沌映射生成初始位置。

混沌映射具有良好的拟随机性、非周期性、遍历性，常用于启发式算法种群初始位置的生成，以使种群尽量均匀分布，从而扩大搜索范围，提高全局收敛性能。本文采用logistic 混沌映射生成HHO 算法的种群初始位置，计算方法详见文献［23］。

3）精英保留策略。

HHO 算法在迭代过程中没有将当前代的种群最优适应度与上一代进行比较，难以保证每一代的种群最优适应度单调不减。针对此问题，本文在每一代位置更新后增加1个判断环节，若当前代种群最优个体位置更新后适应度变差，则不更新该个体位置，从而保证种群最优适应度向理论最优值不断逼近。

4）随机变异。

为降低HHO 算法陷入局部最优的风险，引入个体随机变异机制，若变异后个体的适应度更优，则将该个体位置更新为变异位置，如式（9）、（10）所示。

4.2.2 MHHO算法在SVM参数优化中的应用

采用MHHO 算法优化SVM 参数的关键点在于个体维度及适应度函数的设置，其中哈里斯鹰个体设置为2 维向量，分别对应SVM 的误差惩罚参数C和高斯核宽度σ。适应度函数如式（11）所示。

综合本节分析，基于HS-MHHO 算法的过采样器与分类器参数双层优化算法流程见附录A图A3。

5 算例分析

5.1 算例样本及参数设置

本文共搜集到979 条变压器故障样本数据，其来源主要有国家电网公司监测数据以及公开发表的刊物、文献等。将所有样本划分为训练样本和测试样本，样本数量分配情况如表1所示。

本文算例在CPU 型号为Intel Xeon Gold 2.70 GHz、内存为256 GB的计算机上进行测试。SMOTENND 算法中，若近邻数L、K取值过大则难以筛查噪声少数类样本，若取值过小则难以充分反映少数类样本的周围样本分布情况，本文取常用经验值5［16-17］。HS算法中，过采样倍率β优化范围取［0，1］，为保证β整体搜索的遍历性与快速性以及β局部搜索的精细度，整体搜索步距Δβw取0.1［15］，局部搜索步距Δβp取0.01。由表1 可知，在Δβp=0.01 的情况下，局部搜索点每前进一次，过采样样本数量仅增加1 个，从而达到最大精细度。MHHO 算法中，优化范围、迭代次数上限G、种群容量H对算法性能有重要影响。若取值过大则算法收敛慢、计算效率低；若取值过小则算法搜索能力差，容易陷入局部最优。本文对上述参数均取常用经验值，其中SVM 误差惩罚参数C的优化范围取（0，100］，SVM 高斯核宽度σ优化范围取（0，10］，G取100，H取30［11-12］；为使分类器对少数类及多数类样本具有同等的泛化能力，3 种适应度指标权值αAcc、αSen、αSpe均取1/3。

5.2 过采样倍率对诊断模型的影响

5.2.1 过采样倍率训练结果分析

采用本文算法训练变压器故障诊断模型，具体训练结果如表2 所示，其中展示的子分类器即为附录A 图A2 中HDAG-SVM 结构的7 个二分类器。由表1 可知，子分类器SVMT／D的原始训练样本集已平衡，因此无需进行过采样，对应表2 中的过采样倍率β为0。

表2 诊断模型训练结果Table 2 Training results of diagnostic model

由表2 可知，除SVMT／D外，其他子分类器的最优过采样倍率均小于1，可以在充分强化少数类样本数据特征的同时，尽量避免引入噪声样本。训练阶段采用留一法验证的准确率基本都在90%以上，说明本文所提双层优化方法效果较好。各子分类器的训练用时均在0.5～2 h 范围内，训练用时不同主要是由各子分类器原始训练样本数量及不平衡度差异造成的，同时也受训练期间计算机CPU 及内存占用情况的影响。由于变压器故障诊断模型的训练过程是离线的，因此表2中的训练用时是可以接受的。

为进一步展示过采样倍率的训练效果，以SVMT1／T3为例，绘制其过采样倍率搜索过程中下层适应度的变化曲线，如图2所示。

由图2 可知，在整体搜索过程中，下层适应度在β=0.9 处达到峰值0.934。进一步地，局部搜索在β为［0.8，1］的范围内进行。在局部搜索过程中，下层适应度在β=0.87 处达到峰值0.943，即为最终的优化结果。从整个搜索过程看，随着过采样倍率的增大，下层适应度逐渐增大，达到峰值之后略有减小。这说明过采样倍率的增大使得少数类样本的数据特征不断增强，当过采样倍率达到一定值后少数类样本数据特征的可强化空间趋于饱和，此后继续增加倍率并不会使得下层适应度有明显增大，反而可能引入噪声样本导致分类性能下降。

5.2.2 不同过采样倍率的诊断测试对比分析

为验证不同过采样倍率对诊断模型分类性能的影响，设计3组算例CE1—CE3。CE1的过采样倍率取为5.2.1节的优化结果，CE2不进行过采样，CE3中各子分类器的过采样倍率均取1，其余参数设置与5.1 节相同。分别采用CE1—CE3训练所得的诊断模型对379 个测试样本进行诊断分类，得到混淆矩阵如图3所示，准确率及诊断用时如附录A表A1所示，379个测试样本的具体诊断结果如附录A表A2所示。

由图3 及表A1 可知：CE1的整体准确率及各类样本的准确率均在90%以上，且明显高于CE2、CE3的各项准确率。这说明与不进行过采样和完全平衡过采样相比，对过采样倍率进行优化后的故障诊断模型具有更强的故障样本区分能力；CE1—CE3的诊断用时均在1 s 以内，体现了故障诊断模型的高效性。

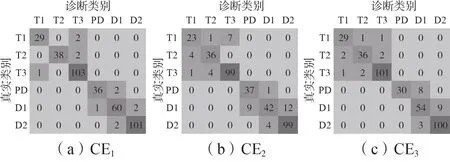
图3 算例CE1—CE3的混淆矩阵Fig.3 Confusion matrix of CE1 to CE3

由表A2 可知，存在极少一部分样本，采用本文方法及其他对比方法（包括后续的算例）都无法对其进行正确识别。可能造成该现象的原因主要有2种：一是采样装置、监测系统、数据记录等本身具有一定的误差，导致记录的样本与其故障类型实际上并不匹配，从而产生诊断错误；二是现有的样本指标体系不足以完全刻画变压器的故障特征，需要增加新的指标以完善故障诊断模型。

5.3 过采样方法对诊断模型的影响

为验证不同过采样方法对诊断模型分类性能的影响，另设计2 组算例CE4、CE5与CE1进行对比。相较于CE1，CE4、CE5的过采样方法分别为SMOTE 算法、ADASYN 算法，2 种方法的近邻数均取5。除上述设置外，CE4、CE5的其他设置与CE1相同。

5.3.1 不同过采样方法的过采样样本分布对比分析

分别对CE1、CE4、CE5的诊断模型进行训练，以各算例的子分类器SVMT1／T3为例，采用t-SNE 算法对不同过采样方法的高维过采样样本分布情况进行降维可视化，CE1、CE4、CE5的过采样样本分布分别如图4、附录A图A4、图A5所示。

由表1 可知，SVMT1／T3的少数类训练样本为T1故障样本。由图4、图A4、图A5 可知，3 种过采样方法均围绕T1 原始样本生成过采样样本，以增强T1原始样本的数据特征。然而，SMOTE、ADASYN 算法生成了大量与T1 原始样本重合的过采样样本，这部分样本不具有数据增强价值，造成了过采样冗余。且上述2种方法的过采样样本均围绕T1原始样本呈小团体式、紧凑式分布，难以改善T1原始样本的内部稀疏问题。相比之下，SMOTE-NND算法的过采样样本在T1原始样本小团体之间建立联系，降低了T1原始样本分布的内部不均匀程度，提高了过采样质量。

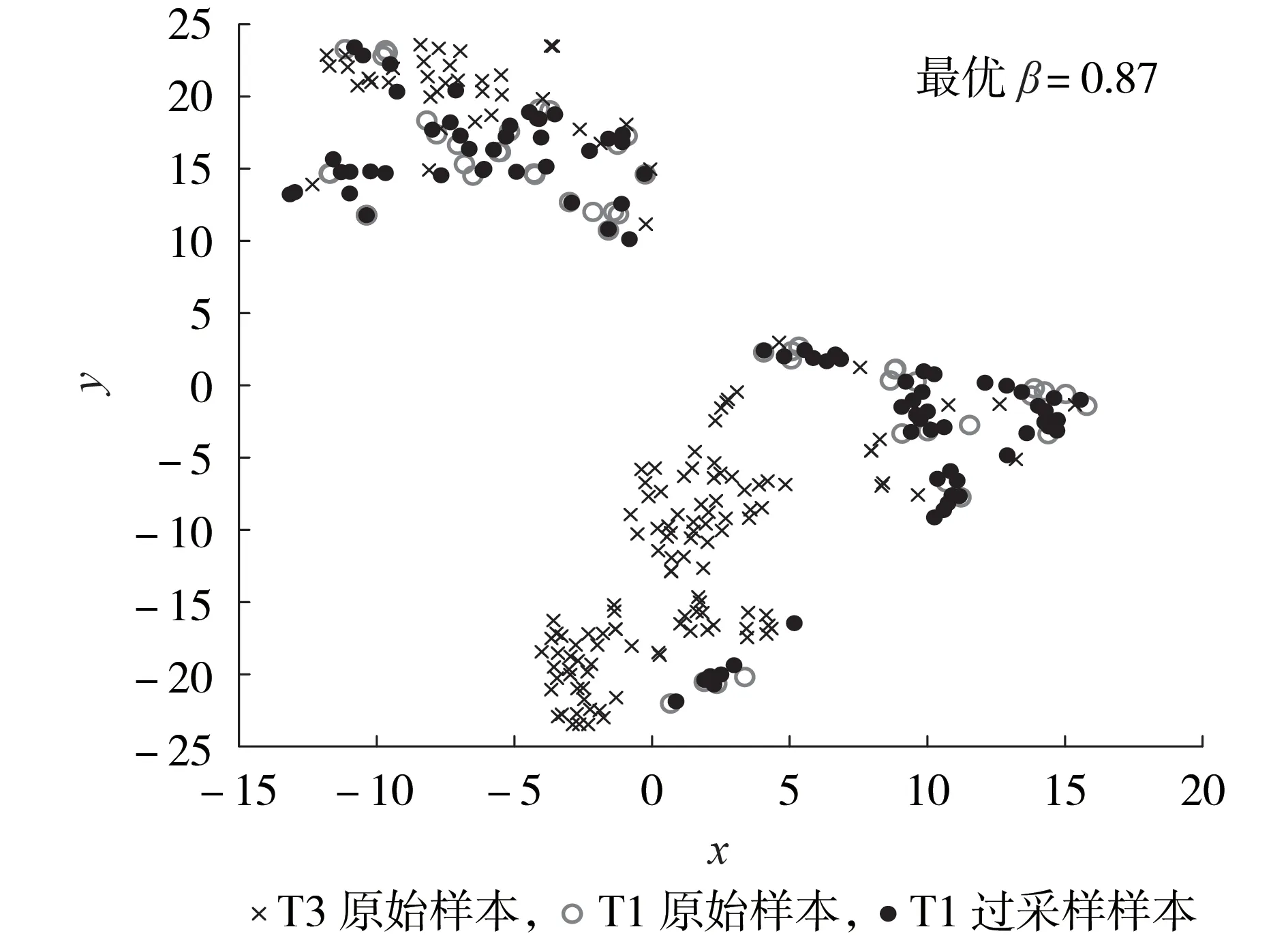
图4 算例CE1（SMOTE-NND算法）的过采样样本分布图Fig.4 Oversampling sample distribution of CE1（SMOTE-NND algorithm）

5.3.2 不同过采样方法的诊断测试对比分析

分别采用CE1、CE4、CE5训练所得的诊断模型对379 个测试样本进行分类，得到混淆矩阵如图5 所示，准确率及诊断用时如附录A表A1所示，379个测试样本的具体诊断结果如附录A表A2所示。

由图5 及表A1 可知，CE1的各项准确率均优于CE4、CE5，这说明SMOTE-NND 算法通过降低合成噪声风险、强化类边界、强化少数类样本内部稀疏区等措施，使得生成的过采样样本质量高于SMOTE、ADASYN 算法生成的样本，从而训练得到分类性能更强的诊断模型。

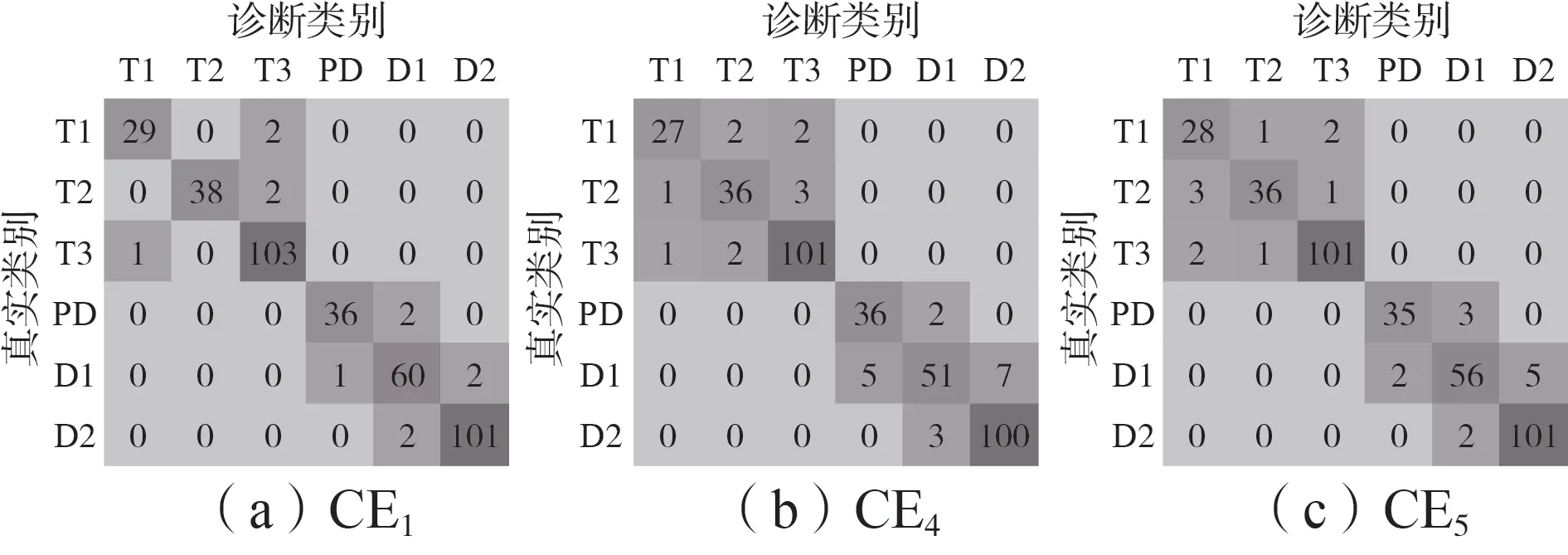
图5 算例CE1、CE4、CE5的混淆矩阵Fig.5 Confusion matrix of CE1，CE4 and CE5

5.4 参数优化方法对诊断模型的影响

为验证不同参数优化方法对诊断模型分类性能的影响，另设计2 组算例CE6、CE7与CE1进行对比。相较于CE1，CE6、CE7的下层SVM 参数优化方法分别为标准HHO 算法、粒子群优化（particle swarm optimization，PSO）算法，HHO、PSO算法的种群数量、迭代次数上限均与5.1节相同，PSO 算法的自我学习因子、群体学习因子均取2。除上述设置外，CE6、CE7的其他设置与CE1相同。

5.4.1 不同参数优化方法的优化过程对比分析

分别对CE1、CE6、CE7的诊断模型进行训练，以各算例的子分类器SVMT1／T3为例，CE1、CE6、CE7的寻优过程分别如图6、附录A图A6、图A7所示。

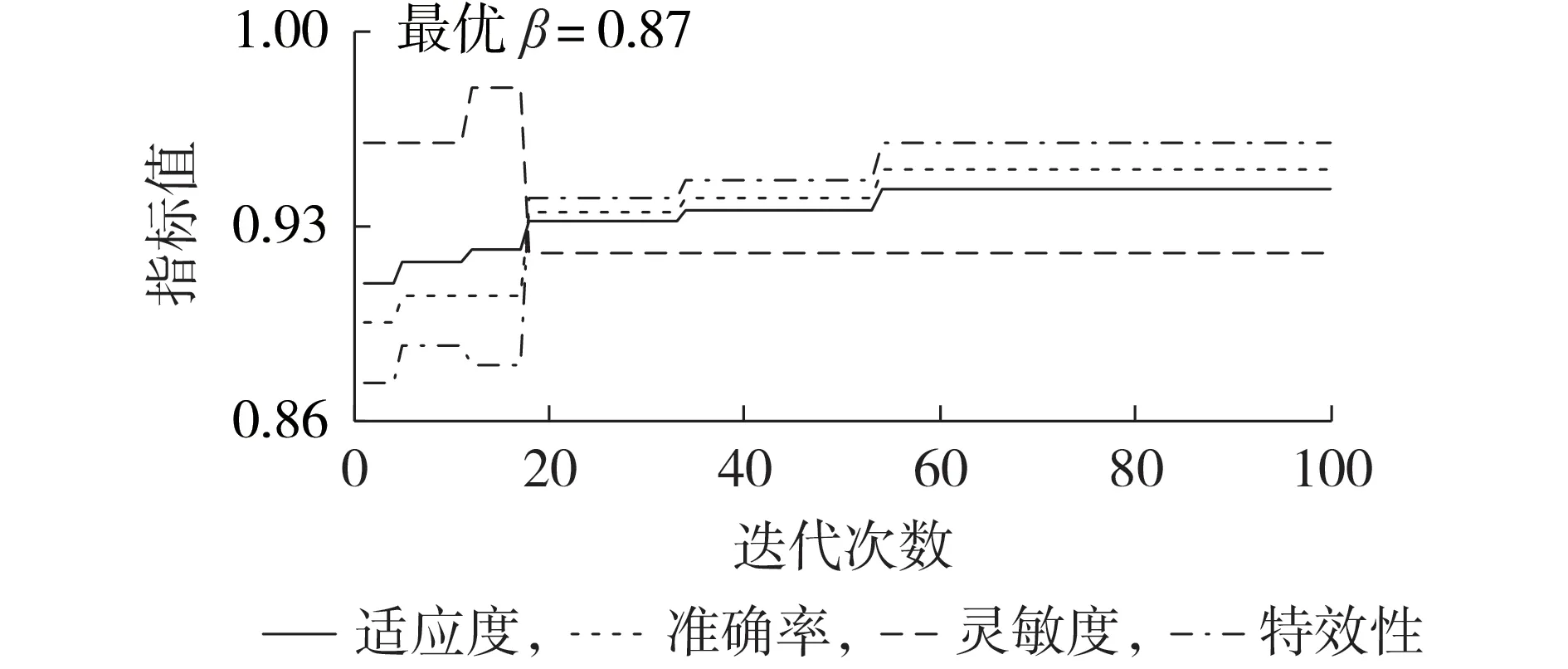
图6 算例CE1（MHHO算法）的迭代过程Fig.6 Iterative process of CE1（MHHO algorithm）

由图6、图A6、图A7 可知，针对SVMT1／T3，3 组算例在各自的最优过采样倍率下分别采用MHHO、HHO、PSO 算法对SVM 参数进行优化，最终适应度优化结果分别为0.943、0.935、0.92，达到最优适应度时的迭代次数分别为54、32、14。这说明MHHO 算法的变异机制使算法进入局部开发阶段后依然有跳出局部最优解的能力，相较于HHO、PSO 算法，算法早熟及陷入局部最优的风险更小。此外，MHHO 算法的初始适应度最高，这是因为logistic 混沌映射生成的哈里斯鹰个体初始位置几乎均匀地散布在算法的搜索空间当中，从而保障了算法的全局搜索性能。

5.4.2 不同参数优化方法的诊断测试对比分析

分别采用CE1、CE6、CE7训练所得的故障诊断模型对379个测试样本进行分类，得到混淆矩阵如图7所示，准确率及诊断用时如附录A表A1所示，379个测试样本的具体诊断结果如附录A表A2所示。

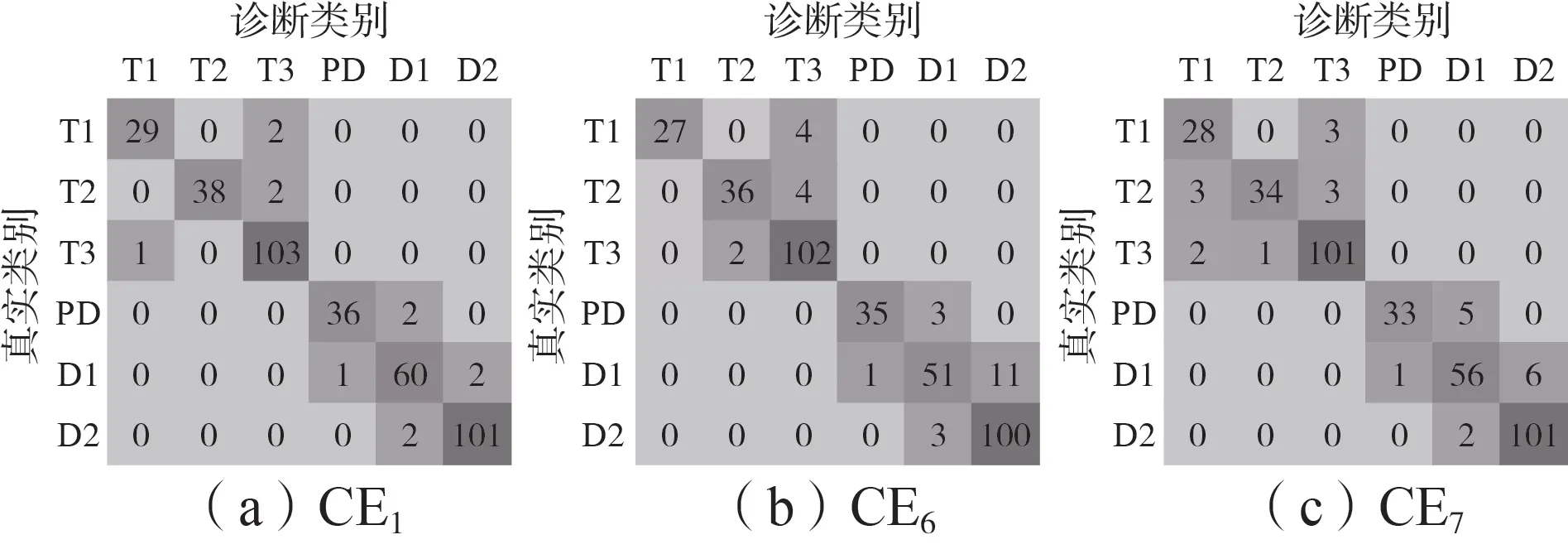
图7 算例CE1、CE6、CE7的混淆矩阵Fig.7 Confusion matrix of CE1，CE6 and CE7

由图7 及表A1 可知，CE1的各项准确率均优于CE6、CE7，这说明MHHO 算法前期全局探索-后期局部开发的最优解搜索模式，配合其变异机制、混沌映射等改进措施，能够有效降低SVM 参数寻优过程中的收敛早熟及局部最优风险，从而能够搜索到使故障诊断模型泛化能力更强的SVM参数。

5.5 基准分类器对诊断模型的影响

为验证不同基准分类器对诊断模型分类性能的影响，另设计2 组算例CE8、CE9与CE1进行对比。相较于CE1，CE8、CE9的基准分类器分别为分类回归树（classification and regression tree，CART）分类器、K最邻近（K-nearest neighbor，KNN）分类器。其中，CART 分类器的待优化参数为最大决策分支数和最小叶节点观测数，优化范围均为［1，50］内的整数；KNN 分类器的待优化参数为近邻搜索数，优化范围为［1，50］内的整数。由于CART分类器和KNN分类器均为二分类器，因此CE8、CE9的多分类策略同样采用层次式有向无环图形式，如附录A 图A2 所示。除上述设置外，CE8、CE9的其他设置与CE1相同。分别采用CE1、CE8、CE9训练所得的诊断模型对379 个测试样本进行分类，得到混淆矩阵如图8 所示，准确率及诊断用时如附录A 表A1 所示，379 个测试样本的具体诊断结果如附录A表A2所示。

图8 算例CE1、CE8、CE9的混淆矩阵Fig.8 Confusion matrix of CE1，CE8 and CE9

由图8 及表A1 可知：除CE9在PD 准确率上略高于CE1之外，CE1的其他各项准确率均优于CE8、CE9，这说明与CART 分类器、KNN 分类器相比，SVM 作为处理变压器故障诊断问题的基准分类器更具优势。CART 分类器、KNN 分类器对T2、D1 等类型故障样本分类性能较差，且存在T、D 大类故障样本间错分的问题，在诊断用时方面也略高于SVM，因此不适合用于变压器的故障诊断。

6 结论

针对变压器故障样本不平衡导致的故障诊断准确率低、诊断效果偏向多数类样本的问题，本文提出一种考虑过采样器与分类器参数优化的变压器故障诊断策略，所得结论如下。

1）与不进行过采样及完全平衡过采样相比，最优倍率过采样能够充分强化少数类样本的数据特征，且降低引入噪声的风险，可有效提高过采样合成少数类样本的质量。相较于不进行过采样及完全平衡过采样的诊断模型，测试样本诊断准确率分别提高了8.18%、4.49%。

2）本文提出的SMOTE-NND 过采样方法能够尽量避免合成噪声，降低少数类与多数类的边界模糊度，降低少数类样本内部分布的不均匀程度，从而合成高质量的少数类样本。相较于采用SMOTE、ADASYN 算法进行过采样的故障诊断模型，测试样本诊断准确率分别提高了4.22%、2.64%。

3）本文提出的基于MHHO 算法的下层SVM 参数优化方法，收敛性能良好，不易陷入局部最优，使得优化后SVM 的泛化能力更强。相较于采用HHO、PSO 算法进行下层SVM 参数优化的诊断模型，测试样本诊断准确率分别提高了4.22%、3.69%。

附录见本刊网络版（http：//www.epae.cn）。