一道含有全称、存在量词的函数题易错分析
刘晓洁, 张启兆
(1.太湖高级中学,江苏 无锡 214125;2.青山高级中学,江苏 无锡 214062)
函数作为高中数学内容的一条主线,对整个高中数学有着重要的意义,每年高考都将其作为必考题.含有全称量词与存在量词的不等式成立问题,也是高考的高频考点,考生在遇到这一部分试题时常常出现错误.本文以一道含有全称、存在量词的函数题为例,对不理解全称量词与存在量词的含义、不会将不等式等价转化等易错问题进行剖析,并提出了一些教学启示.
1 题目呈现
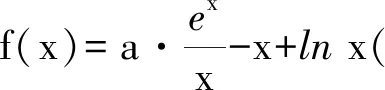
( )
(2022学年苏锡常镇四市高三教学情况调研数学试题第12题)
这道题目设计新颖,尤其是题中给出的全称量词与存在量词使许多学生出错,某市市区平均得分1.51,其中全部选对(得5分)的人数占12%,部分选对(得2分)的人数占43%,是一道区分度较高的试题.
2 思路探究
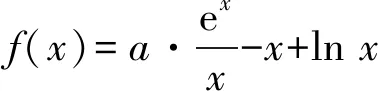
易错1问题的等价转化.
对f(x)求导,得
易错2不会将f′(x)转化成适当的积的形式.
1)a≤0,当0
易错3忽视对参数a的分类讨论.


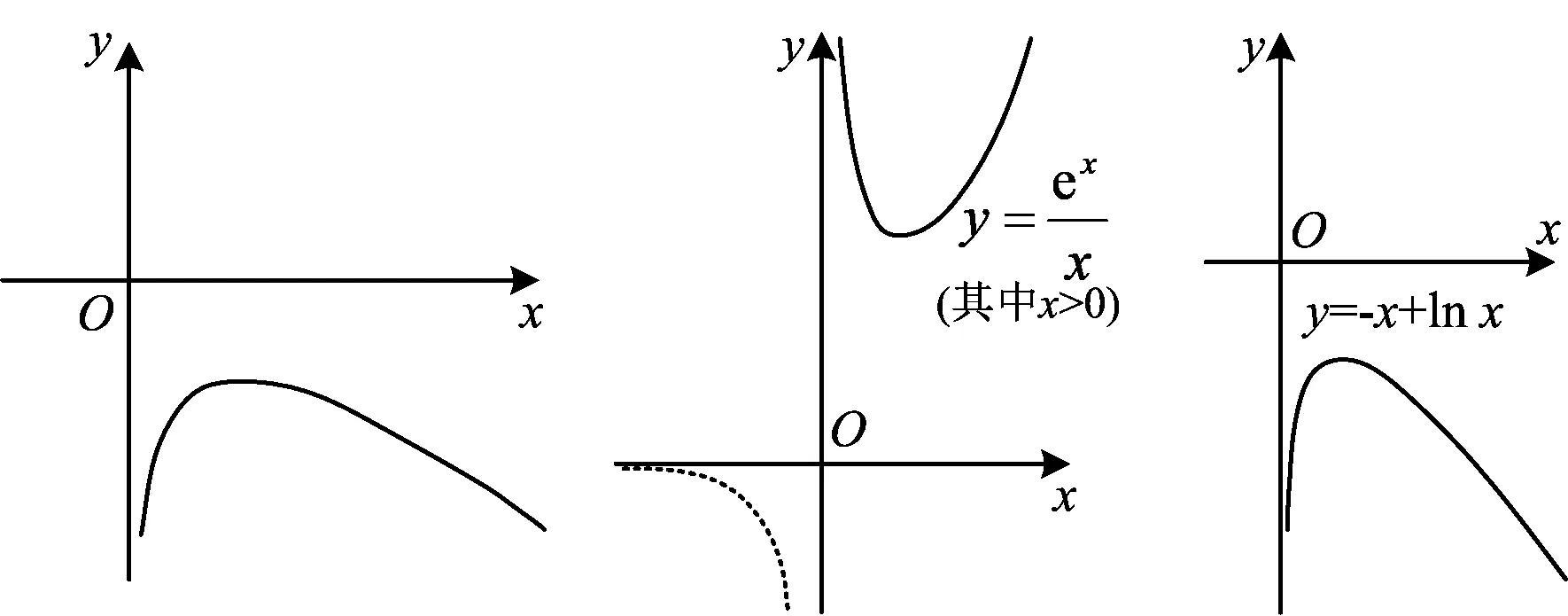
图1


易错4不会虚设零点x1,x2.

综上所述,实数a的取值范围是a≤0,因此选项中满足条件的实数a的可能值有-1,0.故选A和B.
易错提醒含有全称量词、存在量词的同一函数的不等式成立问题,关键是将含有全称量词和存在量词的条件“等价转换”:
形如“对任意x1∈A,都存在x2∈A,总有f(x1) 形如“对任意x1∈A,都存在x2∈A,总有f(x1)>f(x2)成立”等价于“函数f(x)在A上没有最小值”. 问题等价于g(t)=at-lnt(其中t≥e)在[e,+∞)上无最小值. ①当a≤0时,g(t)在[e,+∞)上单调递减,当t→+∞时,g(t)→-∞,符合题意. 综上所述,实数a的取值范围是a≤0,因此选项中满足条件的实数a的可能值有-1,0.故选A和B. 分析3(同构+特殊值法) 对于选项A:当a=-1时,h′(t)<0,h(t)在[e,+∞)上单调递减,无最小值,故A正确; 对于选项B:当a=0时,h′(t)<0,h(t)在[e,+∞)上单调递减,无最小值,故B正确; 对于选项D:当a=1时,h′(t)≥0,h(t)在[e,+∞)上单调递增,h(t)有最小值h(e),故D错误. 分析4(检验法)考虑到本题是多选题中的压轴题,可以使用代入检验法. 易错7解答多选题的方法不灵活,不会用检验法. 因为求的是a的取值范围,而给出的4个选项是具体的数值,从选项的判断来说,优先选B(因为a=0,f(x)最简单),画出函数f(x)=-x+lnx的图像(如图2),发现它不存在最小值,符合题意. 图2 图3 图4 该题是多选题的压轴题,难度较大,从考试结果来看,得分率也极低.本题以指、对数函数为载体,综合考查导数的应用,以及含有全称量词、存在量词的不等式成立问题的转化策略,题干简约,背景新颖,对数学抽象、逻辑推理、数学运算等数学核心素养有较高的要求.许多学生一见到此题,就被“吓住”了:函数解析式中既有指数函数又有对数函数,有两个参数,还有全称量词、存在量词,做题的信心也就不那么足了!笔者分析主要在如下4个方面存在问题. 1)不理解全称量词与存在量词的含义.“若对于定义域内的任意实数s,总存在实数t使得f(t) 2)审题时没有注意到本题中只有一个函数,而误以为是两个不同的函数,套用结论“已知函数y=f(x)(其中x∈[a,b]),y=g(x)(其中x∈[c,d]).若对任意x1∈[a,b],存在x2∈[c,d],有f(x1) 4)不会利用分类讨论、数形结合思想. ( ) 分析由题意可知函数f(x)无最大值. 综上所述,a≤0. 分析根据定义可得函数h(x2)在[0,2]上的值域包含函数y=2a-x1在[0,2]上的值域,再借助a值的唯一性即可推理计算作答. 评注若对任意的x1∈[a,b],存在x2∈[c,d],有f(x1)=g(x2),则f(x)的值域是g(x)值域的子集. 例1重视基于数学素养的关键能力的考查,在数学知识层面、数学能力层面和创新思维层面都有所体现,对数学教学具有重要的启示意义. 重视基本知识和技能的学习,注重过程,让问题探究成为课堂的中心与主线,从而拓展知识的深度,提升思维品质,培养创新意识,进一步提高素养,这是一个循序渐进的过程.布鲁纳曾说:“我们教一个科目,不是去建立一个有关该科目的小型图书馆,而是要学生自行思考,像一名数学家那样去思考数学,像史学家那样去探索历史,投入获得知识的过程中去.”[1]如果教师在准备高三数学复习课时能多在学习策略、思考方法和探索途径上下功夫,用“问题串”驱动学生思维,促进学生深度学习,那么高三数学复习才会有“跳出题海”的希望,进而达到培养学生思维能力的目标. 2022年的数学高考试题坚持“引导学校和学生减少死记硬背和‘机械刷题’现象”,再一次启发教师要转变育人方式,重视学生的主体作用与合作探究,坚决摒弃课堂教学“满堂灌”;重视新教材中的“拓广探索”“探究与发现”,引导学生建立知识体系,促进学生将知识和方法内化为自身的知识结构;重视从以教为主转向以学为主,要精准分析学情,精心设计数学探究活动;重视自主探索、动手实践、合作交流、阅读自学等多种学习方式,以达到提高复习效率、提升学生“四基”(基础知识、基本技能、基本思想、基本活动经验)和“四能”(发现问题能力、提出问题能力、分析问题能力、解决问题能力)的目的. 从更大视角、更高位置,用基本思想、经验、方法进行整体教学设计和教学实施,重视主题教学、深度学习.教育不再是单纯的知识识记,更注重知识在头脑中与原有知识的重新建构与知识系统在实践中的迁移与创新.学生在深度教学的课堂中,强调对知识理解的深度.对于教师教授的知识,学生在结合自身已有知识体系与经验的基础上,进行再次建构,有利于学生建立良好的认知图式,强化知识,促进迁移[2].深度学习更重视及时引导学生对认知结构中已有的一些解法进行反思与提炼,掌握正确的学科思想方法,培养独立思考的能力和创新意识,帮助学生建立起对一类问题的整体认知,进而生成处理一类问题的基本方法、基本经验.




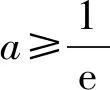





3 错因分析

4 易错练习

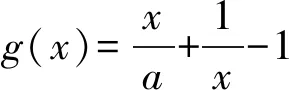




5 教学启示
5.1 注重过程,提升思维品质
5.2 转变角色,教为主转向学为主
5.3 改变教学方式,重视主题教学、深度学习

