潜孔冲击器非线性动力学建模

冯 定，赵 钰，孙巧雷，王健刚，吴何洪

(1.长江大学 机械工程学院，湖北 荆州 434023；2.湖北省油气钻完井工具工程技术研究中心，湖北 荆州 434023；3.中石化石油机械股份有限公司，湖北 武汉 430223；4.苏州新锐合金工具股份有限公司，江苏 苏州 215127)

引言

潜孔冲击器是潜孔钻机的重要组成部分，随着经济的飞速发展和科技的不断进步，广泛用于冶金、化工、水利、矿山、基建等领域[1-2]，是当今不可或缺的凿岩工具。冲击器是通过高压气体驱动内部活塞高频往复运动并撞击钎头，最终实现破岩和钻进。现阶段潜孔冲击器的核心技术主要由国外公司掌握。因此，需要深入研究潜孔冲击器的非线性动力学，为该工具的国产化提供理论基础和研究手段。

国内外针对潜孔冲击器也进行了相关研究。自20世纪80年代起，徐小荷[3]开展了冲击凿岩工具理论与电算研究。进入21世纪后，由于计算机技术的快速发展，张志兵[4]、熊青山等[5-6]和刘权萍[7]基于VB或C++等编程语言，研发了具有可视界面的潜孔冲击器辅助计算及设计程序，用来计算潜孔冲击器的相关性能参数。江涛等[8]和何小宏等[9]利用MATLAB及其系统仿真工具，建立了潜孔冲击器的性能计算程序。卜长根等[10-11]将在潜孔锤活塞非线性动力学理论与LS-DYNA仿真软件相结合，分析了冲击器的破岩过程，并基于Hertz理论，分析碰撞过程中的瞬态动力响应。近年随着对潜孔冲击器的标准与要求的不断提高，越来越多研究人员对潜孔冲击器进行了结构优化。HUANG Yong等[12]重点分析进气量与冲击器性能之间的关系，确定最小进气量与深度、压力等参数的关系。BO Kun等[13]通过计算机模拟和辅助设计，对潜孔冲击器进行了结构优化，并通过现场实际运用进行了验证。KIM D J等[14]基于潜孔锤气动动力学模型，对潜孔锤的性能进行数值模拟和评估，并通过试验进行了验证，最终提出了提高潜孔锤冲击性能的优化方案。杜成[15]基于冲击系统模拟模型，对气缸进行了局部结构优化。张晨[16]利用正交分析试验对后气室排气长度、后气室压缩长度和后气室进气长度进行优化。

国内外针对潜孔冲击器的研究较多，但现有理论中针对潜孔冲击器的充气与排气阶段的气室压力计算大都基于孔口质量流量方程进行计算，该模型中忽略了气体的压力、温度对密度的影响，最终得到的压力曲线与实际值存在一定误差。为深入研究潜孔冲击器的非线性动力学，本研究以无缸潜孔冲击器为例，以流体力学、计算流体力学为基础，考虑气体的压力、温度与密度变化影响，建立了基于二阶麦科马克差分格式的气室充气与排气的瞬变流模型；考虑活塞的运动对气室体积的影响，基于气体绝热方程，建立了气室膨胀与压缩的绝热模型；基于应力波传递理论，考虑活塞、钎头和岩石的材料特性，建立了活塞与钎头的撞击回弹模型；联立上述3个模型，结合活塞的运动方程，根据潜孔冲击器1个运动周期内的11个阶段中的活塞与气室状态，建立了完整的潜孔冲击器非线性动力学模型；最后，利用该模型针对实际算例进行计算，发现活塞的运动参数结果和气室压力数值变化规律与潜孔冲击器的工作原理与运动学规律一致。本研究对潜孔冲击器的设计与研发方面提供研究基础与方法，为相关工具的动力学模型和仿真模型的建立提供参考。

1 结构及工作原理

无缸潜孔冲击器，即无气缸参与其配气过程的潜孔冲击器，具体结构如图1所示。该工具主要通过中心配气杆、活塞和外套管进行配气。高压气体通过逆止阀后，进入中心配气杆；高压气体通过中心杆开孔与活塞内部流道之间的结构配合，进入前气室或后气室，对前气室或后气室进行充气增压，驱动活塞开始返程或冲程运动；当活塞返程或冲程一段位移后，由于中心杆开孔、活塞内部流道、外套管直接的配气结构配合，对应的气室充气通路关闭，此时由于前气室或后气室中压力仍然较大，活塞继续做返程或冲程运动；当活塞返程或冲程继续一段位移后，由于中心杆开孔、活塞内部流道、外套管直接的配气结构配合，另一端气室的气体通路打开，对后气室或前气室进行充气增压；与有缸潜孔冲击器类似，在一端气室充气增压时，另一侧的前气室或后气室与活塞、钎头内部流道相连，气体经过活塞和钎头的内部流道从钎头头部的排气孔排出；排气孔排出的气体对钻井过程中钎头破碎的岩石碎屑进行吹渣，将碎屑从环空排至地面。

1.后接头 2.密封圈 3.外套管 4.矩形胶圈 5.逆止阀体 6.逆止阀座 7.弹簧 8.定位销 9.密封圈 10.配气杆 11.配气塞 12.活塞 13.导向套 14.保持环 15.前接头图1 无缸潜孔冲击器结构图Fig.1 Structure of DTH hammer without cylinder

2 流道模型简化及研究假设

2.1 流道模型简化

根据潜孔冲击器结构及工作原理可知，高压气源从中心配气杆进入潜孔冲击器活塞内部气体通路，然后根据活塞与外套管之间的气路进入活塞前部的前气室中。此过程为前气室充气增压过程，为方便后续建立动力学理论模型，将各不同气路看成同轴圆管流道，各个圆管流道直径及长度按照实际过流面积及长度进行转化。因此，图2中的前气室充气过程可以看成气体通过不同直径的圆管进入最后的气室中，最终前气室的充气过程可以看成高压气体进入低压串联变径管路，且管路下游为盲端。

图2 气路几何模型简化Fig.2 Simplified diagram of inflation process of air chamber

2.2 研究假设

潜孔冲击器受高压气体作用，驱动活塞轴向往复运动并撞击钎头，钎头受到轴向脉冲力对岩石进行破碎，最终实现破岩效果。在这个工作过程中，活塞的受力及运动非常复杂，从理论计算角度对其进行全面精确建模十分困难，但为合理的描述冲击器内部动力学过程，求得适合实际工程需要的参数，可以通过忽略次要因素，保留描述冲击器动力学过程的主要因素，从而简化计算。因此，做以下假设：

(1) 冲击器内部高压气体为理想气体；

(2) 前、后气室内膨胀、压缩时气体变化过程为绝热过程；

(3) 冲击器内部气体的热力过程为准静态过程；

(4) 活塞运动过程中铅直；

(5) 忽略摩擦阻力；

(6) 忽略潜孔冲击器旋转。

3 运动学分析

潜孔冲击器在工况下，高压气体间歇性进入前、后气室中，前、后气室中存在的压力差驱动活塞往复运动。而在活塞的不同运动阶段和不同前气室、后气室状态下，活塞的受力及运动均不同。如图3所示，活塞在整个运动过程中受到重力G、前气室压力p1和后气室压力p2，在运动过程中活塞加速度(沿冲击器钻进方向为正)为：

(1)

式中，A1，A2—— 前气室、后气室压力沿轴向作用在活塞上的面积，m2

m—— 活塞质量，kg

v—— 活塞速度，m/s

g—— 重力加速度，m/s2

图3 冲击器活塞受力分析Fig.3 Stress analysis of DTH hammer piston

活塞运动过程中，前、后气室分别有充气、排气、膨胀和压缩4个阶段。根据活塞的运动状态和气室的气体状态，将整个周期除撞击回弹外分为10个阶段，其每个阶段中的前、后气室根据自身气体状态需采用不同模型及边界条件进行计算，具体的各阶段下的模型状态如表1所示。

4 非线性动力学研究

4.1 气室气体瞬变流模型

基于流体基本方程，即连续方程、运动方程和能量方程，考虑冲击器工作情况下气体的可压缩性，结合气体状态方程，建立气体瞬变流方程组：

表1 前、后气室不同状态下的计算模型Tab.1 Calculation models of front and rear air chambers under different states

(2)

式中，k=1.4为绝热系数，Rg=287 J/(kg·K)为气体常数。

为使计算模型结果与实际潜孔冲击器气室的充气或排气阶段的气体瞬变流更相符，采用麦考马克格式二阶差分方法对式(2)进行求解。麦科马克方法里，对于某个参数Y而言，在i+1时刻的值为：

(3)

则，密度、速度和温度表达式为：

(4)

式中av代表时间导数的平均值，可以用预估值和校正值得到。

1) 预估步

采用向前差分代替方程中的空间导数，连续方程、运动方程和能量方程可转化为：

(5)

(6)

(7)

式中所有i时刻的流动变量均已知，从而式右端是已知的。

现取泰勒级数前两项求预估值，预估值中仅包含泰勒级数的一阶项，只有一阶精度：

(8)

(9)

(10)

2) 校正步

在校正步中，首先使用向后差分代替连续性方程右边的空间导数，然后用预估值进行计算，得到在i+1时刻的预估值分别为：

(11)

(12)

(13)

由于：

(14)

3) 边界条件

(1) 上游恒定压力进口 气室充气过程中，进口为恒定压力状态，假设进口处的密度和温度均为恒定已知。在冲击器气室充气状态下，第1个网格和第2个网格处的截面积A相同，将连续方程中时间和空间采用向后差分进行离散，得到i+1时刻的进口密度：

(15)

同理，通过对运动方程和能量方程进行相同处理，可以得到速度和温度在i+1时刻的进口数值：

(16)

(17)

(18)

同理，通过对能量方程进行相同处理，可以得到温度在i+1时刻的下游封闭处的数值：

(19)

已知下游封闭处的密度和温度，通过气体状态方程可以直接求得压力：

(20)

(3) 上游封闭 在潜孔冲击器前气室和后气室的排气阶段中，上游为封闭状态。此时，在封闭处有：

(21)

由于排气阶段之前为气室的膨胀或压缩阶段，因此上游无恒定压力进口，则封闭处相关数值为膨胀或压缩阶段末的数值，即：

(22)

(4) 下游排气 气室排气阶段中，下游与大气相连，则在下游排气口有：

(23)

式中，p0—— 大气压力

将连续方程和运动方程中的时间和空间的偏导采用向前差分进行离散，得到i+1时刻的下游排气边界上的密度和速度：

(24)

(25)

然后通过气体状态方程求得下游排气边界上的温度：

(26)

4) 稳定性条件

差分方程的稳定性条件指使差分格式稳定所必需满足的条件，即：

(27)

式中，Δt和Δx分别为差分法计算过程中的时间步和网格划分尺寸；v和c指的是速度和波速的标量数值；C为柯朗数；当C≤1时，显示方法计算稳定。但在计算过程中由于v和c均为变化值，为满足稳定性条件，有两种方法：

(1) 在计算过程中固定x，根据v+c数值确定时间步长t，这样每计算一个时间步，重新计算一次t，即t为动态值。动态时间步会使计算结果出现“扭曲”现象，并且使用动态时间步长不能很好地反应流动中实际、物理上的瞬态流场；

(2) 通过计算所有网格处的t，然后取其最小值，这样时间步长为定值后，计算便可以模拟实际中真实的非定常流动，并给出了非定常流的连续方程、运动方程和能量方程相容的实际流场的时间精确解。

4.2 绝热模型

针对气室的膨胀和压缩过程，通过假设认为上述过程中，气室内部气体与外界不参与热量交换，通过气体绝热方程建立对应的计算模型，描述上述过程中气室内的压力、温度、密度等的变化。

绝热过程方程：

pυk=const

(28)

式中，υ—— 质量体积，是体积与质量的比值

根据式(28)可得：

(29)

式中，p1—— 气室膨胀或压缩之前的压力

p2—— 气室膨胀或压缩之后的压力

由于绝热过程中，气室内气体质量不变，体积发生改变，整理后：

(30)

式中，V1—— 气室膨胀或压缩之前的体积

V2—— 气室膨胀或压缩之后的体积

根据气体状态方程p=ρRgT，带入式(30)，整理后有：

(31)

绝热模型式(29)和式(31)可以通过气室体积变化计算得到气室内部压力和温度，能够描述气室的膨胀与压缩过程。将绝热模型与瞬变流模型相结合，即能描述气室在冲击器各状态下的气体压力变化。

4.3 瞬态冲击回弹模型

1) 冲击破岩机理

活塞在高压气体作用下返程、冲程，并最终以一定速度撞击钎头尾部，钎头受到活塞冲击力进行破岩。在活塞撞击钎头并破岩的整个过程中，活塞和钎头的受力急剧变化。为研究上述整个过程，应用波动力学理论，考虑活塞、钎头和岩石的材料特性，建立活塞与钎头的撞击回弹模型。

潜孔冲击器正常工作时，活塞受到高压气体驱动，使活塞周期性以一定速度撞击钎头，活塞动能经过钎头传递至岩石，从而破岩进行钻进，如图4所示。

图4 冲击破岩原理Fig.4 Principle of rock breaking by impact

潜孔冲击器钻进的过程，也是活塞撞击钎头破岩的过程，实质是：活塞撞击钎头产生入射应力波，应力波在钎头中传递，经L/c(L为钎头长度，c为纵波波速)时间后传递至钎头与岩石的接触面；在钎头和岩石接触面处，部分应力波作用在岩石上进行破岩，部分应力波变为反射波，经过相同时间在钎头中反向传递至活塞与钎头撞击面；反射波的一部分传递至活塞，在一定条件下，活塞在此反射波作用下发生回弹。

2) 冲击回弹模型

活塞撞击钎头视为等波阻撞击，此时的入射波表达式：

(32)

式中，P—— 入射波力值，以潜孔冲击器钻进方向为正

m—— 活塞和钎头的波阻

v0—— 活塞的撞击速度

τ—— 撞击持续时间，τ=2L/c

波阻通过公式得到：

m=ρcA

(33)

式中，A—— 活塞或钎头截面积

对于纵波波速：

(34)

式中，E—— 材料弹性模量

大量试验和研究结果表明，钎头与岩石接触的界面处，作用力与位移基本呈现线性关系。因此，将作用力与位移用下列函数表示：

(35)

式中，R—— 作用力

x—— 破岩位移

K，K′ —— 岩石的加载刚度和卸载刚度，取决于岩石类型和钎头种类，令K′=αK，α为卸载系数

由于等波阻，活塞撞击钎头后产生矩形波，当该应力波传递至钎头与岩石接触面时，作用力和位移满足式(34)，入射波和反射波还需满足以下条件：

(36)

式中，Q—— 反射波

根据式(34)、式(35)可以分别得到岩石加载和卸载阶段的方程组：

岩石加载阶段方程组：

(37)

岩石卸载阶段方程组：

(38)

由式(31)和式(36)、式(37)求得反射波：

(39)

入射波传递至钎头和岩石的接触界面时，产生反射波经L/c时间后传递至活塞与钎头的撞击界面。反射波前部分为拉伸波，在该应力波作用下，活塞与钎头分离；当反射波后部分的压缩波传递至活塞与钎头撞击界面，使两者重新接触，反射波进入活塞中，从而使活塞发生回弹。因此，发生回弹的必要条件是反射波使活塞与钎头的撞击面产生的位移大于0，所以回弹判据有：

(40)

将式(38)带入式(39)中，有：

(41)

当活塞撞击钎头破岩系统满足式(41)时，活塞将会发生回弹，否则活塞不发生回弹。

根据动量守恒，活塞回弹的平均速度为：

(42)

式中，ve—— 活塞的回弹速度

τ′ —— 活塞与钎头撞击后至重新接触时间

由下式确定：

(43)

将式(38)带入式(42)即能得到活塞撞击钎头至再次接触的时间：

(44)

若参数满足：

(45)

由式(41)可得：

(46)

将式(38)、式(43)带入式(45)中，在当γ≤1.25，τ′≤τ时得到式(46)，在当γ>1.25，τ′>τ时得到式(47)：

(47)

(48)

式(46)和式(47)即为瞬态冲击回弹模型，可求出活塞撞击钎头的回弹速度。

4.4 非线性动力学模型建立

将气体的瞬变流模型式(14)、绝热模型式(30)、式(31)和撞击回弹模型式(47)、式(48)分别用Y1，Y2，Y3表示；配气长度用L表示，下标分别表示不同阶段的配气长度。由于计算过程中计算量非常大，流程也较复杂，具体求解流程如图5所示，其具体计算流程：

(1) 设定相关结构参数(气室等效作用面积、配气长度等)、工作参数(额定压力、温度、重力加速度等)和计算参数(时间步、网格尺寸及数量等)；

图5 具体求解流程Fig.5 Flow chart of nonlinear dynamics solution

(2) 初始状态下，对赋初值给活塞(位移、速度和加速度)和气室(压力、温度和密度)；

(3) 通过赋初值给活塞和气室，结合活塞的运动方程，判断活塞初始状态；

(4) 开始工作工况后，在第一个时间步，高压气体进入潜孔冲击器内部，根据运动学分析，此时活塞位移s小于此阶段的配气长度L1，判断为前气室充气、后气室排气阶段，因此前气室采用充气增压边界条件的Y1模型(即瞬变流模型)，后气室采用排气减压边界条件的Y2模型(即绝热模型)；

(5) 通过对应模型计算气室中压力、温度和密度等参数后，结合相关等效作用面积，带入活塞的运动方程，判断活塞在第一个时间步末的运动状态。

(6) 如果位移不为0，则重复流程(4)和流程(5)；若位移为0，且速度不为0，即活塞撞击钎头，此时通过撞击回弹模型计算活塞撞击后的运动状态，然后再重复流程(4)和流程(5)。

以上即为潜孔冲击器的非线性动力学模型的具体求解方法。基于潜孔冲击器运动学模型，通过图5中的具体求解流程，联立流体瞬变流模型、绝热模型和瞬态冲击回弹模型，运用编程方法，建立完整的潜孔冲击器非线性动力学模型。

5 实例计算

应用所建立的潜孔冲击器非线性动力学模型，对所设计的6 in潜孔冲击器进行计算。工具进气压力为1.5 MPa，温度为80 ℃，室外压力为标准大气压，温度为20 ℃，相关参数如表2所示。

通过非线性动力学模型计算潜孔冲击器工作0.5 s，分别提取前气室压力、后气室压力、活塞的加速度、速度和位移的计算结果如图6～图10所示。

图6与图7分别为前气室与后气室的压力数值变化，由于活塞在返程后半程和冲程的前半程过程中，后气室的充气气路一直为开启状态，活塞在此过程中先返程减速至0，再冲程加速；而前气室在充气气路开启过程中，由于活塞会以较高速度撞击钎头并发生回弹，因此前气室在充气过程的时间较短；且根据实际气路长度来看，前气室充气气路长于后气室充气气路，在一定充气压力作用下，管路越短，压力波动周期越短，即单位时间内的波动频次更高。综上，后气室充气过程时间长于前气室充气时间，且后气室充气管路短于前气室充气管路，因此前气室压力波动时间短，但波动频率低；后气室压力波动时间长，且波动频率高。

表2 参数数值Tab.2 Parameter values

图6 前气室在0.5 s内的压力变化Fig.6 Pressure change of front air chamber within 0.5 s

对于加速度而言，在返程和冲程过程中分别主要受到前气室压力与后气室压力作用。以钻进方程为正，则返程过程中主要受到前气室作用力(方向为负)，在冲程过程中主要受到后气室作用力(方向为正)，因此反映在图8中的数值变化即为：在负数部分曲线与前气室最大压力波动规律相似，在正数部分与后气室最大压力波动规律相似。

图7 后气室在0.5 s内的压力变化Fig.7 Pressure change of rear air chamber within 0.5 s

图8 活塞加速度在0.5 s内的变化Fig.8 Piston acceleration change within 0.5 s

图9 活塞速度在0.5 s内的变化Fig.9 Piston velocity change within 0.5 s

将数据进行处理后可知，在1.5 MPa的进气压力作用下，在0.5 s内完成了约12.5个周期，即频率约为25 Hz；前气室在充气阶段压力最高约1.62 MPa，后气室在充气阶段压力最高约1.84 MPa；活塞加速度在返程过程中最高约416 m/s2，在冲程过程中最高约782 m/s2；在第一个周期内，活塞的速度返程和冲程过程中最高约5.89 m/s和8.4 m/s，由于在第一个周期末活塞与钎头撞击发生回弹，因此在后续的多周期中速度会高于第一个周期，返程速度最高约6.25 m/s，冲程速度最高约8.64 m/s；活塞在第一个周期内，返程至最大处的位移为82 mm，在后续多个周期由于活塞撞击钎头反弹，使活塞返程的最大位移提高至85.7 mm，活塞位移小于配气长度L4，即还未达到表1中返程的最后一个阶段(前气室排气、后气室压缩)活塞就开始冲程。

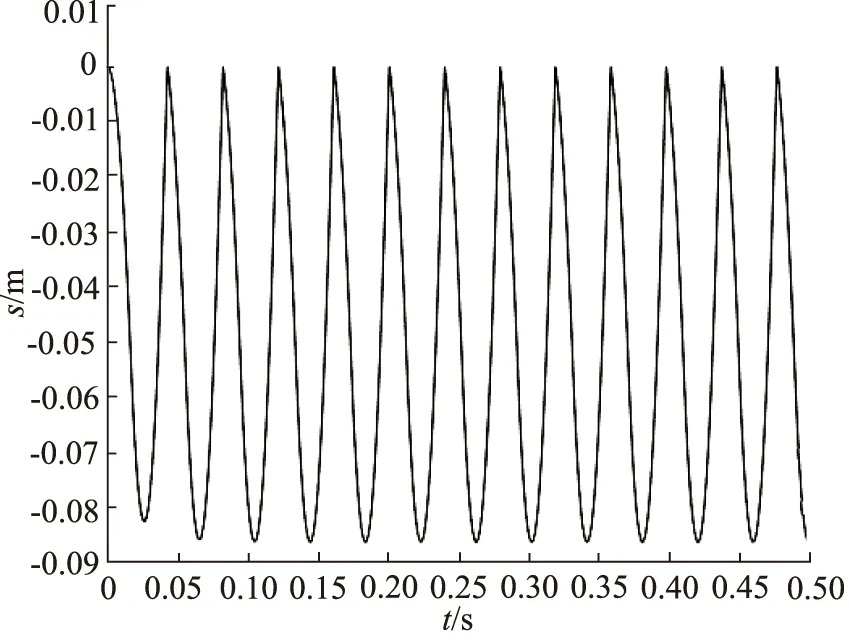
图10 活塞位移在0.5 s内的变化Fig.10 Piston displacement change within 0.5 s

6 模型对比

现有潜孔冲击器的动力学模型中，采用孔口质量流量方程描述气室的充气与排气过程，方程如下：

气体处于亚音速流动状态时，其质量流动方程为：

(49)

气体处于超音速流动状态，其质量流动方程为：

(50)

式中,A—— 气体流动截面积

pi，pj—— 上、下游气体绝对压力

Ti—— 上游绝对温度

以前气室压力为例，通过两个不同动力学模型分别进行计算后，取1个运动周期内的计算结果，如图11所示。

图11 前气室压力计算结果对比Fig.11 Comparison of calculation results of front air chamber pressure

对比发现，现有动力学模型中，由于忽略空气的可压缩性，导致充气阶段压力迅速增加，达到1.5 MPa的进口压力后保持不变；在排气阶段，压力降低过程中，同样由于忽略气体的可压缩性，现有动力学模型得到的压力变化曲线不存在压力波动，降低至大气压后保持不变。

本研究改进后的动力学模型，考虑空气的可压缩性，在充气与排气阶段，压力变化更符合实际规律，得到的最终性能参数计算结果也更贴近真实值。

7 结论

(1) 本研究主要对潜孔冲击器进行了运动学分析，根据不同阶段中的气室的不同状态，建立了描述充气和排气过程的气体瞬变流模型与描述膨胀和压缩过程的绝热模型；根据活塞与钎头的碰撞过程，建立了瞬态冲击回弹模型；最后整合上述各模型，建立了能够描述潜孔冲击器实际工作情况的非线性动力学模型；

(2) 通过实际算例，利用非线性动力学模型进行计算，计算结果符合潜孔冲击器原理与运动学规律，与现有动力学模型进行了对比，发现改进后的动力学模型由于考虑了空气的可压缩性，其计算结果更符合实际；

(3) 本研究针对潜孔冲击器所建立的非线性动力学模型，为该工具的国产化提供理论基础和研究手段，为同类气动工具提供理论参考。