仿鳐式软体驱动器弯曲预测方法的研究

李 旭，刘 胜，徐青瑜，张远飞，霍前俊，张耀耀

(上海工程技术大学 机械与汽车工程学院，上海 201620)

引言

在自然界中，研究人员从大自然的生物，如蛇的身躯[1]、大象的鼻子[2]、章鱼的触手[3]等获到了启发，设计出区别于传统刚性结构机器人的新式机器人，简称软体机器人，其在结构上具有高自由度转变且能够连续形变的特点[4]。研究人员一般使用杨氏模量较低的柔性材料[5]制作软体机器人，此材料柔化性好、易制备，环境适应能力强。软体机器人按照驱动源可划分为智能材料驱动、磁场驱动、流体驱动和其他驱动四大类[6]。考虑到经济成本、环境保护且便于实现等原则，软体机器人通常选择大自然中质量轻、易获取、无污染的空气作为动力源进行驱动。软体机器人结合了传感技术[7]、3D打印技术[8]及新式的智能材料[9]等相关技术，同时还涉及了结构力学、控制工程等学科，是一个新兴的研究热点。

气动软体驱动器由其构成的材料、几何构形、气腔结构、气腔数量决定驱动器的驱动力与变形的行程。常见类型的软件驱动分类包括束缚纤维、形状记忆合金[10]、复合智能材料和线驱动器[11]。其中，气动束缚式纤维具有输出的末端力大、启动迅速的特点，因而普遍适用于软体机器人。在纤维增强型软体驱动器方面，POLYGERINOS等[12]为加强型的纤维软体驱动器提出了分析理论模型，为研究软体驱动器模型建立提供了方法；根据应力应变理论和Yeoh模型[13]，费燕琼等[14]建立气动爬行机器人的压强与路程的预测理论模型；在多模块结合驱动方面，南京航空航天大学团队研究多模块驱动器的弯曲变形与气压的关系，提出了一种预测3段串联的气动软体驱动弯曲变形程度[15]的理论模型。

目前，多数软体驱动器针对其气腔形状的研究为等截面形态[16]，而对于变截面的研究却少有涉及。本研究从鳐鱼的运动受到启发，设计了一款气腔截面纵向变换仿鳐式软体驱动器。为了研究其力学性能，设计的驱动器限制层附有不可压缩的薄层，结合应变能密度等理论，提出了一种预测驱动器的弯曲变形角度的方法。同时使用3D打印技术制作模具，浇注模型，制作出软体驱动器。通过理论分析、有限元仿真、实验对比验证其数学模型。为软体驱动器能空间上高精度，高自由度的工作做出了准备。

1 仿鳐式软体驱动器的设计

软体驱动器的设计仿生鳐鱼，如图1a展示了鳐鱼的运动轨迹的走向，基于此设计了仿鳐式软体驱动器探究鳐鱼的运动形态，模拟其运动轨迹，如图1b所示驱动器由两部分组成：带有腔室的主体结构和底部具有一定厚度的限制层黏合而成。在顶层结构中，含有多个腔室且按循序排列，腔室之间由一条气路联通，腔室密闭与外界环境无交互通气。底层的限制层较厚，能够有效地防止其膨胀。其结构设计如图1所示。

图1 仿鳐式软体驱动器仿生来源Fig.1 Bionic source of faux Manta soft drive

考虑到软体驱动器通气后表面的膨胀影响其弯曲功能以及在其工作时产生不符合其预期的结果，使软体驱动器同时具备形变变形的稳定性和弯曲的有效性，将软体驱动器进行优化，如图2所示。

图2 仿鳐式软体驱动器结构优化Fig.2 Bionic source of faux ray soft drive

图2a中腔道为通用型腔道，气体通过通气平层链接各个腔室，通气后表层膨胀不能进行有效弯曲。图2b为改良结构，将气腔内部链接各个腔室的通气平层改成通气管道，减少了非必要的形变与表层膨胀，效果更好，优化后变量斜体的结构特征如图3所示，软体驱动器设计参数数据如表1所示。

2 矢量方程构建预测模型

仿鳐式软体驱动器采用硅胶材料浇注而成，这种材料具有超弹性，其形变时呈现非线性，大变形的特征。因为属于大变形，软体驱动器采用Yeoh模型作为预测驱动器在工作时的弯曲特性的本构模型，同时超弹性材料的各向同性和不可压缩性，应变能密度函数表达式为：

图3 变量斜体软体驱动器结构图Fig.3 Bending deformation coordinates of actuator

表1 变量斜体软体驱动器设计参数Tab.1 Soft actuator design parameters

W=W(I1,I2,I3)

(1)

(2)

式中，λ1，λ2，λ3—— 软体驱动器在空间上3个方向的伸长比

I1，I2,I3—— 级数展开式

由于所使用的硅胶材料具有不可压缩性，有J=I3=1，因此式(1)可写为经典的应变能密度函数两项展开式：

W=C10(I1-3)+C20(I1-3)2

(3)

式中，C10，C20—— 基于Yeoh模型的材料常数；可取为C10=0.14，C20=0.00086。

由Cauchy-Green，Piola-Kirchhoff分别提出的应变张量定义、应力张量，硅胶材料的应力-应变关系可由应变能密度对其主应力求偏导得：

(4)

所以主应力ti与应变λi之间的关系为：

(5)

考虑软体驱动器工作时轴向应力与应变关系时，t2=t3=0。

(6)

由上式中，

(7)

通入气压，软体驱动器弯曲变形图如图4所示。

由图4可知软体驱动器在外气压作用下分为形变部分和非形变两部分，图中所示得驱动器m，n部分处无空腔，不发生形变，而中间l0为主要的形变结构，建立几何关系图。

图4 驱动器弯曲变形图Fig.4 Drive bending deformation diagram

在工作区间中驱动器限制层厚度较高，且限制层加持了不可压缩得薄层，因而可设定限制层底部在气压作用下限制层长度l0不变，由图3可得，驱动器轴向的伸长比，驱动器变形后底面弧长与中间弧长的几何关系为：

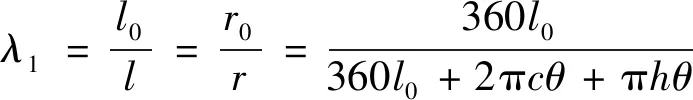
(8)

式中，l—— 变形后驱动器中间层弧长

l0—— 驱动器底面弧长

r—— 驱动器变形后中间层弯曲半径

r0—— 驱动器变形后底层弯曲半径

θ—— 驱动器弯曲角度

软体驱动器弯曲变形后，轴向横截面积与初始横截面积可由s=s0λ2λ3计算获得[17]。依据软体驱动器截面形状构建力平衡方程，推导出主应力与驱动气压之间的关系：

(9)

将式(7)～式(9)代入式(3)求得弯曲角度与驱动气压之间的关系：

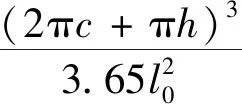
(10)

3 预测模型的实验及仿真验证

3.1 仿真材料设定

为了制备具有形变功能好，环保无污染的软体驱动器，选择具有良好弹性的硅胶材料。硅胶在外力作用之下呈现非线性的几何变化，常用能级的变化表达出此材料的力学性能。现有研究常用Mooney-Rivlin模型和Yeoh模型这两种应变能密度模型。Mooney-Rivlin模型一般用于硅胶材料小变形的场景，而Yeoh模型用于硅胶材料的大变形。故仿鳐式软体驱动器选择Yeoh模型作为在通入气压时的力学模型。

3.2 样机实验

1) 仿鳐式软体驱动器的制作

仿鳐式软体驱动器主要由上半部分的腔式结构和底层的限制层组成。考虑到浇注的便捷和脱模的易取，制作仿鳐式软体驱动器先制作其内部腔道和外部形变的腔壁，再与限制层结合。制作过程如图5所示，模具1经过浇注后形成仿鳐式软体驱动器的上层腔体，然后浇注模具3且安置导气管，最终将上层腔体与限制层一同封膜，得到一个密封性良好的软体驱动器。

图5中使用三维软件进行设计模具的结构，然后通过3D打印机对模具进行打印，模具使用的材料为光固化树脂，最终打印完成的模具如图6所示。

使用图6所示树脂模具进行浇注和装配。浇注材料为液态硅胶与其固化剂按照50∶1的比例搅拌均匀，浇注在模具上，凝固所用时间为30～60 min，最终可得到固态的硅胶实物。

2) 实验平台的搭建

为了准确的测量仿鳐式软体驱动器在不同的气压下的弯曲变形程度，需要配备的实验条件为：可调节大小的气压源、传输气体的导管、显示刻度的量程装置、气压的量值、固定整个装置的设备，实验平台如图7所示。

图6 3D打印制作的模具Fig.6 Mold made by 3D printing

图7 实验平台Fig.7 Experimental platform

相关实验的操作过程:首先打开气泵开关，控制调节气压阀，控制进入驱动器的气压大小。带有一定气压的气体通过气管一部分流入了气压表，一部分流向仿鳐式驱动器使其形变。记录气压表上的气压值与相对应仿鳐式软体驱动器在网格刻度板上的弯曲角度，最终得到数据的对比。

3.3 实验验证

实验检验仿鳐式软体驱动器的弯曲变形程度，将其中的理论模型的计算、软件仿真结果与实验的力学特性进行比较，检验其结果的差异程度。在实验过程中，以仿鳐式软体驱动器作为实验的对象，对其施加p为0.02～0.07 MPa的稳定气压，记为p2～p7，采样区间的差值为0.01 MPa。

记录实验数据，同时测量驱动器的变形轨迹。在同一气压下，仿鳐式软体驱动器的实验结果与仿真结果对比如图8所示。

实验过程中记录软体驱动器的弯曲变形轨迹，采用高清相机进行图像采集，然后将采集的图像与驱动器的弯曲变形理论模型、有效元仿真的数据进行对比。取软体驱动器在各个气压下的弯曲后形成的中心线代表软体驱动器本身，如图9所示，选取0.03，0.05，0.07 MPa气压点下进行比较实验。

图8 驱动器弯曲实验结果Fig.8 Actuator bending experimental results

由上图可以看出，理论模型、仿真数据与实验数据计算结果基本一致但还存在一定的误差。误差产生有以下3点原因：

(1) 所使用的硅胶材料建立理论模型时选择Yeoh模型，在软体器形变程度较大时，有限元分析的准确度也会降低；

(2) 制造仿鳐式软体驱动器时，浇注会产生细小的气泡，气泡无法完美除去；同时在制造的过程中驱动器的尺寸也不易把控，降低了实验的精准度，从而产生相应的实验误差；

(3) 在实验过程中，气压的大小、气压的稳定性在相对范围内是保持不变的，但并不是绝对的恒定，从而造成实验的稳定性不足。

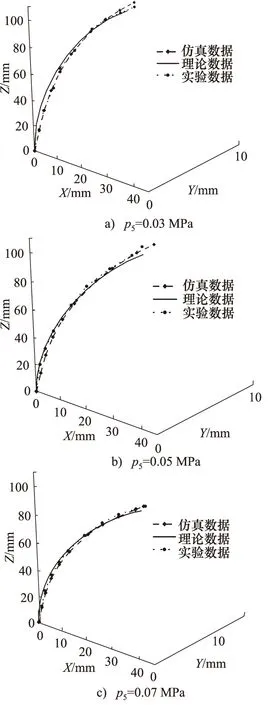
图9 变形轨迹对比图Fig.9 Deformation trajectory comparison chart

搭建软体驱动器输出力的测试装置，分析输入的压强与仿鳐式软体驱动器的关系，如图10所示。调试测试装置相对位置，并对数字秤进行校零。

分别向软体驱动器输入气压p，p取0.02～0.07 MPa，记录相对应的输出力F，如图11所示为输入的气压与末端输出力的关系。

4 结论

(1) 设计了一款仿鳐式软体驱动器，实现了软体驱动器空间弯曲的功能，同时优化了驱动器的结构与功能；

图10 驱动器末端输出力测量装置

图11 驱动器输入气压与输出力的关系Fig.11 Relationship between air pressure and output

(2) 基于Yeoh模型，同时与限制层无变形、应变能密度等理论相结合，提出了一种预测仿鳐式软体驱动器弯曲变形的方法；

(3) 使用3D打印技术制作模具，浇注模型，制作出软体驱动器。通过理论分析、有限元仿真、实验对比验证其数学模型基本准确，为研究变截面软体驱动器弯曲变形提供了一种方法。