基于数学核心素养的小学代数思维培育探索

高友润

（福州教育学院附属第三小学，福建 福州 350008）

随着“双减”政策落地及《义务教育数学课程标准（2022 年版）》的颁布，减轻学生学习压力、提高教学质量、落实核心素养已成为当前小学数学教育的重点。代数思维是由关系或结构来描述，通过数学符号、字母等研究运算规律、探析数学性质，是一种数学推理运算的过程。当教学新的数学概念时，代数思维推导模式主要体现在归纳与推理、模式化与结构化等活动中，有利于发散小学生数学思维，提升小学生的数学综合能力，培养学生符号意识和数感等素养。然而，在日常教学过程中，大部分数学教师将算术与代数“分而治之”，导致代数思维与算术思维的培养与引导割裂开来，不利于小学生数学思维的发展和数学核心素养的培养。

一、理清代数与算术的异同，明晰代数思维概念

数学是一门严谨、抽象，且注重思维方式的学科。在数学教学过程中，需要将核心素养贯彻落实到教育的每一个阶段，引领学生不断提升数学认知能力、数学思维水平。小学生学习数学时，首先接触的是具体的数的运算，并逐步形成相对稳定的算术思维。代数运算则是以算术运算为基础，针对抽象符号的运算。在引领小学生建立代数思维的过程中，教师要将算术与代数联系起来，引入逻辑关系，使得学生能借助现有的计算规律和方法，了解什么是代数、领悟代数与算术之间的差别，从而进一步加深他们对代数思想和概念的认识。

例如，在“乘除”算理知识点教学中，教师应改变以往直接灌输计算规律相关知识的做法，利用启发式、探究式等教学方法，探索算式中的逻辑关系，逐步建立树立代数观念。如将算式“4×25=100”变式为“4×（ ）=100”，利用乘法和除法之间的关系，引导学生思考未知数与“4”和“100”之间的关系，由此引入“代数”的概念。然后，在此基础上，发挥信息技术的教学优势，利用多媒体播放动画，创设问题情境：小羊想要渡过一条河，水獭们就搭建了一座桥，在小羊过河的时候，水獭们却说：“你要过河，就要先回答问题！”小羊想了想，就点了头。水獭出题：4×（ ）=36，5×（ ）=100，6×（ ）=42。当童话故事演示完后，教师就可以顺势说：“让我们来帮帮想要过河的小羊吧！”引导学生参与算式思考与计算过程之中。但与以往不同的是，要引导学生理解与运用代数思想，需先让小学生讲述他们的思考过程，再结合实际题目，说说如何利用代数求解，帮助学生理清算式中的代数关系、逻辑关系，引导学生认识与应用代数思维。

二、创设问题情境，培养代数思维意识

《教育部2022 年工作要点》明确提出，“实施教育数字化战略行动。强化需求牵引，深化融合、创新赋能、应用驱动，积极发展‘互联网+教育’，加快推进教育数字转型和智能升级。”党的二十大报告指出：“加推进教育数字化，建设全民终身学习的学习型社会、学习型大国。”信息技术革命给世界的发展带来了翻天覆地的变化。现代技术与教育教学相融合是教育信息化、现代化的必然趋势，是构建高质量教育体系的重要途径，也是办好人民满意的教育的必然要求。代数思维的本质是一种关系思维，它的形成过程是一种从常量到变量的符号化、形式化或结构化的过程。教师可以运用信息技术多种感官同步进行的特点，创设问题情境，提供丰富感知，调动已有经验，运用其中的逻辑关系，培养学生代数思维意识；也可以运用信息技术，创设形象化、生动化的互动情境，积极地与学生互动，适时进行思维引导，提升学生的代数思维意识。

例如，教学“用字母表示数”的时候，首先，运用信息技术，创设扑克排序游戏情境：卡通扑克牌6、7、8、9、10 依次从屏幕中挑出排队，首先问学生：“下一个应该谁出场？为什么是‘J’出场？”“猜猜再接下来出场的是什么？说说为什么是J、Q、K 出场？”让学生初步感知可以用字母表示一个特定的数。其次，运用信息技术创设数列填数游戏，体验用字母可以表示任何数。教师依次出示卡通数字数列：（1）5 6 7 8 B 10 11 12……；（2）2.5 2.7 2.9 3.1 H 3.5……；（3）……教师让学生来说一说数列中的字母表示的是什么？引导学生明确可以用字母表示整数、小数、分数，这些数都是确定的数，也可以说固定的数。再次，运用信息技术继续创设动画游戏情境——“一猜即中”：小精灵往魔盒里放若干彩球，同学们猜放了几个彩球？要求“一猜即中”。学生猜测后，教师问：“一定吗？”学生自然回答：“不一定。”教师又问：“为什么？”学生回答：“因为不知道老师放入了几根。”这时候，教师启发：“有没有一个数一定能表示老师信封袋中的粉笔数量呢？”这时有学生想到：“字母n。”教师进一步启发：“你怎么能想到用n 根表示呢？”学生：“生活中不确定的数都说n个。”就这样，逐步调动学生已有经验，引导学生运用其中的逻辑关系，突破“字母可以表示未知数”的认知难点，感悟数学代数思想。最后，借助信息技术出示一条可延伸的数轴》（见图1）：

图1

教师问：“这里的“m”表示多少呢？”

学生回答：“m 表示11”。

教师又问：“如果□里的数也用字母表示，你想用什么来表示？”

学生又想到：n，p，y……

这时，教师要增加难度。

问学生：“如果□不能用其它字母表示，只能用‘m’来表示，该怎么表示？”并进一步师引导：“能不能用与’m’有关系的式子来表示呢？动动脑筋想一想。”

同时，借助放大镜突出数轴中我们要观察的部分，引导学生让学生观察数轴

教师问：m 表示哪个数？□表示哪个数？11 和8之间有什么关系？11 和9 之间相差多少？11 用m 表示，那8 该怎么表示呢？

在此基础上，让学生自己在数轴上找一个数，并用含有“m”的式子表示；之后，让学生思考，从刚才的活动中你有什么发现？引领学生一起经历用含有字母的式子表示数的过程，进一步经历字母可以与数一起组成式子表示一个数，感知用含有字母的式子表示一个数。创设形象化、生动化的互动情境，积极地与学生互动，适时进行思维引导，提升学生的代数思维意识。

三、联系生活实际，注重代数思维应用

教育家陶行知提出“日常生活即教学”“社会即学习”和“教学做合一”。日常教学中，教师要注意引导学生利用观察到的生活现象、面临的生活问题等，学会用数学的符号和语言探索建立与数学之间的联系，培养代数思维的应用意识。代数思维的训练具体可从以下几个方面入手（见图2）。

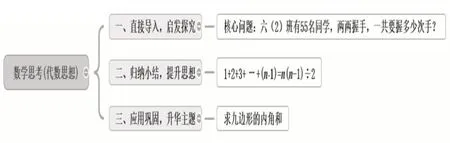
图2

（一）给学生提供探究的空间

苏霍姆林斯基指出：“在人的心灵深处，都有一种根深蒂固的需要，这就是期望自己是一个探究者、发觉者、研究者，而在儿童的精神世界中，这种需要特别强烈。”如教学“以退为进”这一课，可以让学生自己动手操作，通过画一画、填一填、说一说，启发学生思考：增加次数＝之前的人数＝人数-1，探究发现规律：1+2+3+...+（n-1）=n（n-1）÷2，激发学生的学习兴趣，加深对所学内容的理解。让学生在活动中体验，在体验中领悟，由具体到抽象，由易到难，从而自然过渡、水到渠成。

（二）注重学生的思维提升

皮亚杰认知发展理论认为，7-12 岁是儿童具体运算阶段，该阶段的运算虽然还是零散的、孤立的，但是在具体事物和情景的支持下，小学生开始能理解符号的意义。逐渐形成抽象逻辑思维。因此，在小学阶段，教师应根据儿童认知与思维发展规律，加强学生代数思维的培养，提升学生数学思维。例如，如有意识地培养学生以退为进的数学思想。导入环节时巧设握手环节（2 个同桌握手、3 个女生握手），紧扣教材例题，同时让数学课饶有生趣。这样在课前制造一个悬疑，不仅激发了学生学习欲望，同时为探究“化难为易”的数学方法埋下伏笔。在探讨55 人握手问题的算法时，同样延用以退为进的思考方法，先探究3 个点时总线段数怎么计算，之后列出4 个点和5 个点时总线段数的算式，让学生观察发觉这些算式的共有特征：都是从1 依次加到人数减1 的那个数，从而让学生明白总次数其实就是从1 依次连加到人数减1 的那个数的自然数的数列之和。接着，让学生用已建立的数学模型去推算55 个点一共可以连成多少条线段。这样既巩固了算法，同时回应了课前游戏的设疑。在此过程中，少部分学生认为，总次数＝上一次次数+增加次数，而没有对自己的算法进行优化。此时，教师可适时引导，应及时更新算法。然后，在算法拓展提升中寻求背后的意义，即（现在的人数×之前的人数）÷2＝总次数。

代数思维是中小学数学的链接点之一，小学生只有在小学时期形成良好的代数思维，才能在今后的数学学习中更好适应教学环境与教学阶段的变化。鉴于此，小学数学教师要以落实数学核心素养培育为前提，重视小学生代数思维培养，并将与代数相关的知识点与算术、算式联系起来，引导小学生结合现有知识、学习经验理解什么是代数，并逐步形成代数思维。