小学数学认知结构的意义与建构

俞丽春

（霞浦县教师进修学校，福建 宁德 355100）

在小学数学教学实际中，有的教师整体意识不强，只关注自己怎么教，而忽视学生具体怎么学；有的教师没有关注学生的已有经验和尊重学生的认知规律，过度关注单个例题的教学；有的教师在数学教学中对小学生的认识结构关注不够，只会进行浅层的、零散的、单一的教学；有的教师没能科学合理地设计问题，对问题设计缺乏整体性和导向性［4］。这些都不利于学生思维能力的发展。现代学习理论认为：新知的获得过程是人对知识主动构建过程，认知结构的零散和不完整，对学生学习的影响是非常不利的。所以，要想提升小学数学课堂教学活动的有效性，不妨从小学生认知结构的建构入手。

一、数学课堂优化中建构学生认知结构的必要性

建构学生的认知结构是优化小学数学课堂教学的有效手段，其必要性主要表现为如下三个方面：

（一）关注学生认知结构是教学的需要

认知结构是一种认知功能体系，它是由知识结构与心理结构共同作用而产生和发展的，它不仅反映了知识在头脑中的储存状态，而且反映出信息的加工方式。［1］现行小学数学教材的编写原则是“逐级递进”与“螺旋上升”，数学教材中的知识结构是符合学生认知结构的，在进行数学知识教学的过程中，教师要注重知识的“生长点”与“延伸点”，把每堂课教学的知识置于整体知识的体系中［2］。

（二）尊重学生认知发展的需要

学生的认知发展指学生的认知能力，随其年龄和经验的增长而不断发生变化的过程，它主要包括感知、注意、记忆、想象及思维等方面的发展［3］。然而，学生的头脑中都有一个知识结构，知识结构的完善程度直接影响着学生对知识的理解、记忆、提取和应用。正如著名心理学家张庆林所说，优等生的知识结构是一张有层次明细的网络图，而学困生的知识结构却是零散的、孤立的。因此，在数学教学中，教师需要建构学生的认知结构，尊重学生认知发展，帮助学生建好知识网。

二、小学生数学认知结构的建构策略

建构小学生的认知结构对数学教学的优化来说意义非凡，那么一线教师有必要加入到对基于学生认知结构的小学数学课堂的构建探索过程中。下面，笔者将结合具体的教学实例，对如何构建基于学生认知结构的小学数学课堂进行论述。

（一）整合教学任务，逐层深化探究

学生对新知的学习需要经历三个阶段：分别是知识输入阶段、相互作用阶段和操作运用阶段。这三个阶段之间层层递进，缺一不可，共同促成了小学生新的数学认知结构的建立。要想在小学数学教学中建构学生的认知结构，教师需整合教学任务，从三个学习阶段入手对课堂认知任务进行细化、优化处理，设计一个符合学生认知结构的数学课堂任务单，让学生在任务单的驱动下深入探究新知。同时，在设计任务单的过程中，教师要尊重学生在任务完成中的主体地位，重视对任务单趣味性建设，以调动学生的认知兴趣。

比如，在苏教版数学四年级上册《简单的周期》一课的学习中，设计了如下三个主要任务：

任务1：男女生记忆大比拼，记扑克牌

以让男女生分组记忆有规律和无规律扑克牌，看哪组记得快的方式推进该活动。让学生们在亲身体验中感知简单周期规律，完成新知、引入任务。

任务2：学生合作探究周期

以提供校园场景图让学生们自主寻找花盆、彩旗、彩灯等物品的排列规律，学生通过独立思考，合作探究，并以多种方法辅助探究，从而总结出“周期现象”的本质特征——依次重重出现。之后，又以解决问题引入周期的应用探究，并以寻找最优解题方法的形式，帮助学生们建立其除法和周期之间的联系。此过程是学生对周期现象探究发现和体验的过程，也是新知与旧知的相互作用过程。

任务3：设计周期

该任务是开放和操作活动，有两个小任务：一个是让学生用△、□和○这三种图形设计一个排列周期，另一个是让学生们观察小动物排队情况，从中发现规律。这两个小任务指向学生对新知的应用能力训练，旨在引导学生进一步体会周期现象的本质特征及分析得出周期规律的观察判断技巧。

在《简单的周期》一课的学习中，设计的任务既以游戏和合作探究为主，尊重了学生的认知地位，也遵循了“知识输入—相互作用—操作运用”这一新知的形成过程，建构了学生的认知特点，帮助学生成功将“周期现象”纳入原有知识体系。

（二）关注已有经验，寻找适宜工具

符合认知结构构建要求的小学数学课堂，是以生为本的自主探索课堂。但受到自身认知基础和能力的限制，小学生在进行新知理解与探究的过程中会遇到各种阻碍。因此，要想让小学生以自主自觉的姿态完成对新的认知结构的构建任务，教师就要尊重学生已有经验，提供适宜的探究辅助工具。

比如，在《小数的意义》教学中，可以选择学生喜爱的几何模型作为辅助工具。

在该知识点教学过程中，可先从旧知入手引入新知，以人民币和长度为载体辅助唤醒学生对0.1 含义的理解后展示直观模型（如图1），深化学生对一位小数含义的理解，帮助学生勾联已有经验，唤起分数和小数之间的联系。

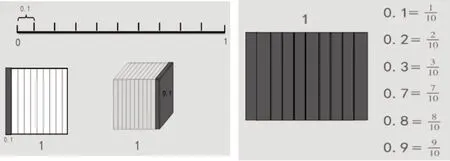
图1 1 和0.1 的直观模型图

之后，又如法炮制，继续借助直观模型图教学0.01 和0.001 作为数的含义。在以直观图模型（如图2）引导学生理解两位小数时，以图为依托引导学生们在“涂一涂、说一说”中理清1、0.1、0.01 之间的内在联系，学会用图表示0.7、0.07、0.70 等多种类型的小数，并感受含义的相同与不同。再借助前面建构的知识经验让学生大胆推测三位小数的含义，以直观图（如图3）辅助学生理解三位小数，并将重点放置到对小数与分数关系的解读之中。与此同时，在该环节结束后，还以针对该部分知识的随堂训练作补充，帮助学生在应用中内化知识。

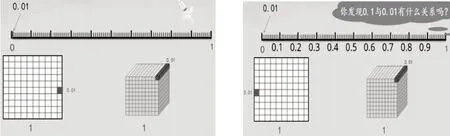
图2 1、0.1 和0.01 的直观模型图

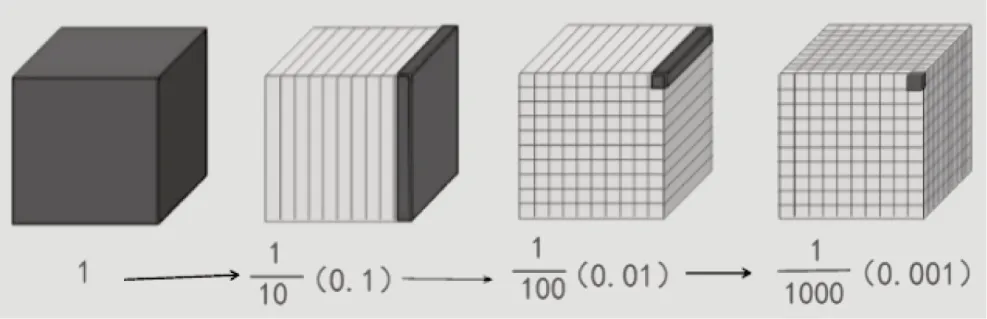
图3 推测0.001 的直观模型图

最后，带领学生扩大研究范围，组织学生依托之前对0.1、0.01、0.001 的直观图（如图4）的观摩经验，分析小数细分的意义和小数的进位制度，并以奥运会田径比赛计时案例作依托，帮助学生进一步领略小数精确性的现实意义。

图4 小数细分的意义和进位制度的直观模

以形助数是有效的数字教学方法，直观模型图是我们辅助学生自觉完成对小数意义的探究任务的合理工具。在这一工具的辅助下，小学生更轻松地将小数的意义融入原有知识网络，建立了新的知识结构。

（三）通过关联整理，感知内在联系

学生知识结构的完善离不开阶段性的知识整理。在单节课中，虽然在教师的有意引导下学生们也能建立起小的知识结构图，但受到具体情境和教学环节的限制，教师教学的内容是零散的、有限的，学生构建的知识结构图并不具备全面性、系统性特点。所以，在阶段教学结束后，教师需要组织面向整个阶段教学的知识关联整理活动，帮助学生感知不同课时所学知识之间的内在联系，建立更大的知识网络图，进一步感受知识间的层级联系。

比如，在《小数的意义和性质》的整理与复习过程中，遵循“联想与整理，沟通与深刻”课堂构建旋律，以展示小数0.88 为例，让学生从具体的数入手，回想单元知识点，再引导学生对知识点进行整理，构建0.88 的联想思维图（如图5）。

图5 0.88 的联想思维图

之后，又让学生们以联想思维图为基准，快速翻阅课本，思考如何对联想思维图中涉及的知识点进行整理，分析探究各知识点之间的内在联系，并以喜欢的方式绘成单元知识结构图，再以相应的提升训练活动作补充，加深学生对小数意义和性质的理解。

在这单元复习中，以整理“两图”的方式帮助学生理清知识间的内在联系，形成完整的、系统的单元知识体系，建立了更完善的认知结构。

（四）注重问题导向，形成整体感知

数学问题是数学研究的起点，是引导学生思维的航标。教师要立足教材，设计富有启发性和适度挑战性的问题，帮助学生不断思考、理清脉络，从而整体感知知识的关键要素。

比如，在《表面涂色的正方体》的教学过程中，以问题串的形式，引导学生自主探究，发现规律。可以从一个大正方体到切成1000 个同样大小的小正方体入手，引出以下问题：（1）1000 个小正方体是不是都涂上了红色？有几个面涂上红色？（2）根据正方体表面涂色情况，可以把小正方体分成哪几类？分别在大正方体的什么位置？（3）如果让你计算出1 面涂色的、2 面涂色的、3 面涂色的小正方体个数，好算吗？计算时会不会有规律？（4）用找一找、数一数、算一算等方法，研究棱长为3 等份，棱长为4 等份，棱长为5等份的小正方体总共个数有几个？3 面涂色，2 面涂色，1 面涂色，小正方体的个数又各有多少个？［5］你能发现什么规律？像这样借助提问的方式，帮助学生自主探究，形成知识间的联系，引导学生经历发现规律的过程，既引起学生的好奇心，又激发了学生的探索欲望，促使学生打开思维，对课堂有一个清晰脉络，并对本该课内容形成整体感知。

通过问题引领，可以帮助学生对知识形成整体感知，遵循知识间的内在联系，以达到教与学的一致，完成认知的结构化。这不仅培养了学生的问题意识，还促进学生学科能力的提升。

综上所述，完善认知结构是优化小学数学教学的有效方法，而要想在数学教学中帮助学生们建立完整的认知结构，教师就需要在以生为本、尊重认知规律、设计适宜的认知活动的同时，提供合适的问题驱动及辅助性认知工具、组织阶段性整理活动，强化对学生的认知结构构建的引导与支持。