考虑节理岩体各向异性的地下洞室围岩稳定分析
周 浩,王小威,刘 晖
(长江勘测规划设计研究有限责任公司,武汉 430010)
1 引言
由于节理、裂隙、断层、软弱夹层等结构存在,天然岩土材料通常具有非常复杂的物理力学特性,常表现出非均匀、各向异性、不连续等特征[1-2]。考虑结构面对岩土材料力学性能的影响,更好地描述岩体变形破坏特征,是目前岩石力学关注的一个重要课题[3-4]。
目前大部分屈服准则基于材料各向同性假设,比如应用最广的摩尔库伦准则、Drucker-Prager准则和Zienkiewicz-Pande准则,这些屈服准则均没有描述结构面各向异性特性对岩体材料强度的影响。国内外众多学者对岩土材料的各向异性特征进行了深入的研究。Jaeger[5]首次提出了层状各向异性屈服准则,并在文献[6]中通过对加载方向的粘聚力修正,实现对摩尔库伦准则的修正,但是并没有考虑内摩擦系数的各向异性特性。在Jaeger粘聚力变化理论基础上,Mclamore等[7]对内摩擦系数和粘聚力进行了修正。Kawamoto等[8]率先引入二阶损伤张量来描述节理岩体复杂结构,曾引起了相关学者的广泛关注。杨强等[9]利用岩体各方向截面的节理连通率定义了二阶损伤张量,建立了节理岩体抗剪屈服准则隐式表达式和具有一阶精度的显示表达式,但引入参数过多,不易确定。
对于岩体工程,节理连通率不仅与节理和节理之间岩桥的强度有关,并且随着剪切方向变化。通常通过节理连通率将完整岩体和裂隙抗剪强度参数加权平均,得到岩体的综合抗剪强度参数,因此,确定岩体各个剪切方向的节理连通率,对研究综合抗剪强度参数非常重要。杜景灿等[10]引入了遗传算法和动态规划来搜索复杂岩体结构面抗剪力最小的结构面组合,从而计算出岩体节理连通率。
本文采用动态规划逆序搜索法和结构面与岩桥破坏理论[11]确定岩体的二维连通率,将基于方向性的节理连通率与抗剪断强度参数引入到各向异性强度准则中。结合岩体层状各向异性的特点,通过三维非线性有限元方法[12],对地下工程洞室厂房分期开挖进行应力计算和稳定性分析,编写了各向异性屈服准则Fortran子程序;结合有限元静力程序,研究岩体材料各向异性强度对洞室围岩应力、变形和破坏区范围的影响。
2 节理岩体各向异性屈服准则
2.1 屈服准则表达式

对于各向同性岩土材料,用应力张量σ表示材料微元体受力状态,法向方向为n的截面上的应力应满足如下条件:

对于各向同性岩土材料,抗剪强度参数f和c为常数,但对于各向异性岩土材料,f和c与截面节理连通率Kn有关。节理连通率反映了结构面对节理岩体抗剪强度的影响程度,将完整岩体与节理材料通过节理连通率加权平均近似求得节理岩体在不同剪切方向的抗剪强度指标:
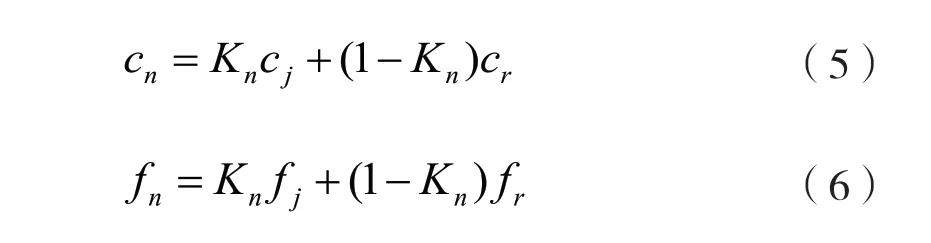
式中:cr,fr为完整岩体的粘聚力与内摩擦系数;cj,fj为节理材料的粘聚力与内摩擦系数。
用cn、fn代替式(2)中f、c,则节理岩体各向异性屈服准则表达式为:
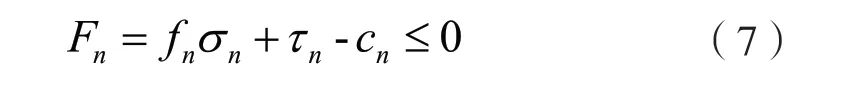
综合式(5)、式(6)、式(7)可知,确定节理岩体各向异性屈服准则的关键在于确定节理岩体沿各个剪切方向的节理连通率Kn。利用文献[7]中提出的动态规划,搜索节理岩体沿各个剪切方向的最小抗剪力路径,可以确定节理连通率Kn。
2.2 动态规划搜索最小抗剪力路径
当岩体发生剪切破坏时,滑裂面部分穿过结构面,部分穿过岩桥,因此岩体的综合抗剪强度由结构面和岩桥共同提供。汪小刚等[11]将节理连通率定义为:岩体沿某一方向发生剪切破坏时,剪切带上结构面节理长度在总的破坏路径长度上所占的比例。

式中:∑JL为破坏路径上节理总长度,∑RBT为破坏路径上岩桥总长度。
岩体结构面与岩桥组合形式基本有三种:重叠但不相交、不相交且不重叠和相交,依据文献[13]和文献[14]中提出的方法对其抗剪力R进行计算,然后采用动态规划逆序搜索法可得到节理岩体沿某一剪切方向的最小抗剪力路径,进而由式(8)求得节理连通率Kn。
动态规划逆序搜索的过程如图1所示。假设需要搜索第5个结构面到第1个结构面的最小抗剪力路径,过程如下:
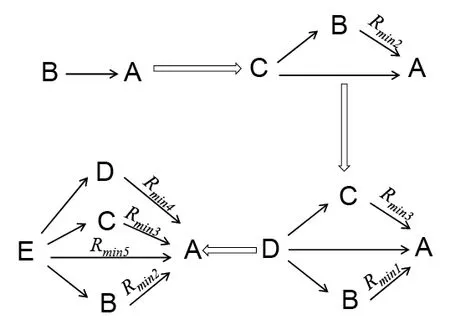
图1 动态规划法搜寻最小抗剪力路径过程
(1)计算结构面B与结构面A之间的抗剪力Rmin2。结构面B与结构面A之间只有一条路径,则结构面B与结构面A之间的抗剪力即为最小抗剪力Rmin2。
(2)计算结构面C与结构面A之间的抗剪力Rmin3,其中有两种情况:①结构面C直接到达结构面A;②结构面C先到达结构面B,然后通过结构面B与结构面A之间最小抗剪力组合路径到达结构面A。此时取两种情况的组合抗剪力最小值为Rmin3。
(3)计算结构面D与结构面A之间的抗剪力Rmin4,其中有三种情况,计算过程同(2)。
(4)计算结构面E与结构面A之间的抗剪力Rmin5,其中有四种情况,计算过程同(2)。Rmin5路径即为第5个结构面到第1个结构面的最小抗剪力路径。
2.3 节理岩体各向异性屈服准则计算
框架见图2,具体求解过程如下。①依据勘测的结构面节理信息模拟生成结构面网络。②节理连通率是一个与方向相关的量,依据结构面与岩桥的破坏理论,按结构面网络中某一剪切方向ni取一合适剪切带,按照2.2节所示的方法,通过动态规划逆序搜索来确定剪切带中结构面和岩桥最小抗滑力组合破坏路径。③计算破坏路径上节理总长度∑JL与岩桥总长度,代入式(8)计算破坏路径上节理连通率Kn。④依据节理信息重新模拟生成结构面网络,按上面步骤重复若干次,得到若干组Kn,求Kn平均数得到最后的剪切方向ni的节理连通率Kn;改变剪切方向ni,重复2.2节中的过程,得到其他各个剪切方向节理连通率Kn。⑤依照式(5)、式(6)求得节理岩体在不同剪切方向的综合抗剪强度参数cn,fn。⑥将cn,fn代入式(7)中,得到节理岩体各向异性屈服准则表达式。

图2 各向异性屈服准则计算过程
3 地下洞室围岩稳定性分析
3.1 层状各向异性岩体力学模式
沉积岩的地下洞室岩体常常表现出层状各向异性的特点,其受力特性与层面的走向和层面的物理力学参数有关,通过层状各向异性的非线性计算方法对其进行稳定性分析。
对于层状各向异性岩体,平行于层面的XY平面物理力学性能是各向同性的,但垂直于层面的Z向与层面有不同的物理力学参数。依据弹性理论,应力应变本构关系见式(9),弹性矩阵见式(10):



图3 局部坐标下层状各向异性岩土材料示意图


3.2 层状岩体非线性迭代
目前地下工程围岩屈服判别中,大多基于岩体材料各向同性假设,这种假设简化了地下工程围岩的物理力学参数,本研究将各向异性屈服准则引入到围岩屈服判别中,使计算结果更符合实际工程情况。
三维层状岩体非线性迭代方法是将洞室开挖荷载分为弹性荷载和塑性荷载两部分,将弹性荷载一次性施加到结构上,塑性荷载分级加载,塑性刚度依据每次塑性加载时结构应力状态来确定。
首先通过屈服准则式(7)求出岩体结构的临界应力,确定弹性荷载系数,将塑性荷载分级加载,按照式(18)进行塑性迭代,由式(19)计算应力增量,然后对平行于层面与垂直层面的破坏状况分别校核拉裂和滑动两种情况。

4 工程应用
某水电站地下厂房洞室群主要由引水洞、主厂房、主变室、母线洞、尾水调压室和尾水洞等组成。总装机量为6×600 MW,主厂房洞室为285.20 m×29.20 m×70.23 m,主变室为255.00 m×18.80 m×33.30 m,设置两个圆筒型尾水调压室,洞高69.00 m,上部直径为40.50 m,下部直径为36.00 m。
地下厂房洞室群围岩主要为厚层状大理岩、角砾状大理岩并夹有绿片岩透镜体,以Ⅲ类为主,厂区发育有断层和节理裂隙等地质构造,岩体材料力学参数见表1。厂区初始应力场实测值较大,为高地应力场。受岩体节理裂隙、地应力的影响,地下厂房洞室群的围岩稳定问题突出。地下厂房洞室三维计算模型见图4。

表1 岩体材料力学参数
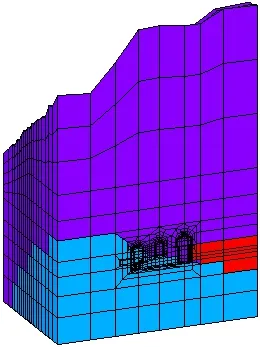
图4 地下厂房洞室三维计算模型
主厂房的锚固支护参数如下。顶拱锚杆:Φ32@1.5×1.5 m,L = 9 m,预应力T = 120 kN的预应力锚杆与Φ32@1.5×1.5 m,L = 7 m的普通锚杆交错布置。边墙锚杆:Φ32@1.5×1.5 m,L = 6 m和L = 8 m的锚杆,交错布置。边墙预应力锚索T = 1750 kN,L = 20 m与预应力锚索T = 1 750 kN,L = 20 m间排布置,@4.5×4.5 m,对穿。喷层厚度:顶拱=20 cm,边墙=15 cm。根据地下厂房洞室群围岩岩性,将岩体材料分为4种类型,分10期进行分期开挖和分期支护计算,有限元分期开挖计算模型见图5。

图5 分期开挖有限元计算模型
由于缺少详细节理信息,假定第一期开挖岩体部分存在一组优势节理裂隙,其参数见表2。给定模型节理连通率来进行分析计算,利用式(5)和式(6)计算出岩桥和结构面综合抗剪强度见表3。
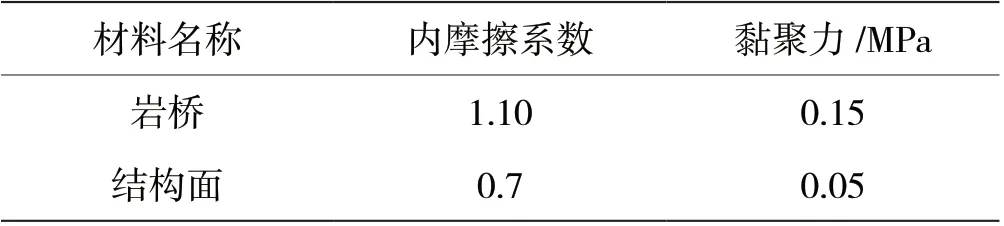
表2 综合抗剪强度参数

表3 岩体各个方向的节理连通率与综合抗剪强度
为了研究层状岩体各向异性强度和各向异性力学性质对地下洞室围岩稳定的影响,编写了各向异性屈服准则Fortran子程序,配合有限元静力程序,进行3种工况下(见表4)的对比分析。

表4 工况计算
3种工况下破坏区的分布规律基本相同,洞室顶拱、边墙中部、洞室交口处塑性破坏区较大。随着开挖的进行,破坏区的发展规律也大致相同。
3种工况下的围岩总破坏量分别为:72.32万m3、87.48万m3、97.20万m3,总破坏量和总耗散能依次增大(见表5)。考虑岩土材料的各向异性后,法向岩体物理力学参数相对于层向围岩较低,各向异性屈服准则抗剪断强度参数小于各向同性屈服准则,工况3相较于工况1围岩总破坏量增加了34%。计算结果规律与一般规律相符合。

表5 开挖完成不同工况围岩破坏指标
3种工况下总破坏量的差异性主要来自于塑性和开裂破坏量的不同,工况1的开裂破坏量小于工况2和工况3,说明岩体材料力学性质和强度的各向异性造成应力集中现象明显。所以按照岩体材料各向同性计算得到的开裂破坏量存在较大偏差。
不同工况下围岩破坏体积随分期开挖变化规律基本相同,破坏量变化速率相差较小(见图6)。前四期开挖量较小,围岩破坏体积相差不大,第五期开挖后,3种工况围岩破坏量表现出明显差异性,说明开挖量越大,考虑岩体材料各向异性越重要。

图6 不同工况下围岩破坏体积变化
图7、图8分别为3种工况下主厂房上游边墙第一主应力和第三主应力随分期开挖的变化。3种工况下第一主应力和第三主应力变化规律基本相同,洞室交口处存在明显的应力集中现象,边墙的应力较大。工况2和工况3较工况1有更显著的突变性,开挖过程中,工况1、工况2和工况3洞周围岩应力大致表现出依次增大的现象,说明岩体材料各向异性对岩体的应力有明显影响。
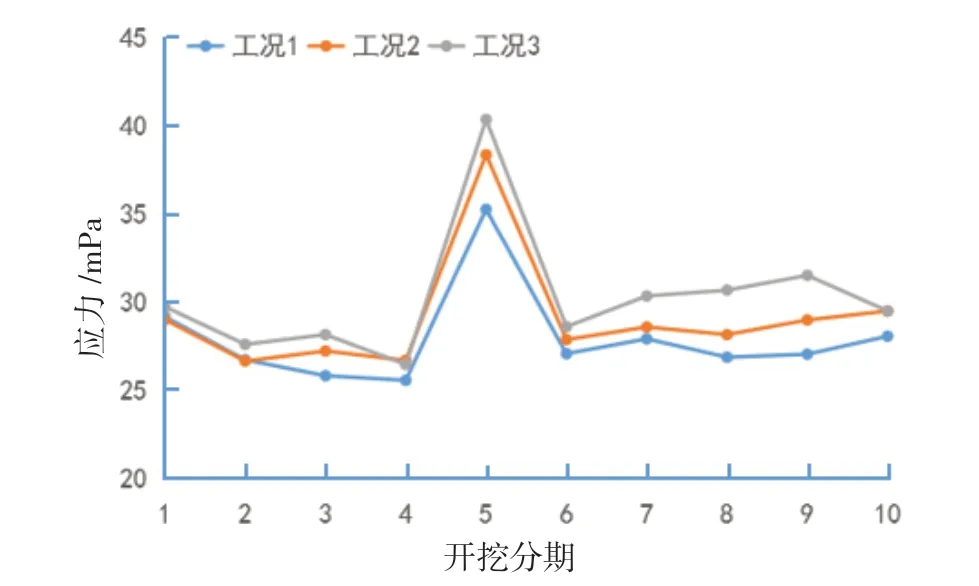
图7 不同工况下洞周第一主应力变化规律

图8 不同工况下洞周第三主应力变化
3种工况下,洞室围岩的变形分布规律基本相同。主厂房边墙的变形较大,体现了大跨度高边墙变形大的特点,边墙最大位移出现在边墙与洞底交口处;洞室顶拱变形较小,顶拱最大位移出现在顶拱中部,沿两边位移递减;洞底有向洞内起拱的趋势。工况1、工况2、工况3上下游边墙位移依次增大(见图9),表明岩体材料各向异性对岩体的位移有明显影响,按照岩体各向同性进行计算可能存在变形预估不足的情况。

图9 不同工况下洞周位移变化规律
在主厂房边墙设置了5个监测点,将3种工况的计算值与监测值进行比较,可以看出,计算值相对于监测值总体偏小(见表6),说明计算过程中对影响岩体变形的因素考虑不足。工况1、工况2、工况3的计算值与监测值接近程度依次增加,工况3计算值与监测值相差较小,说明考虑岩体材料各向异性来进行应力计算和屈服判别,更能反映岩体变形的真实情况。

表6 不同工况各监测点位移 mm
5 结论
(1)考虑岩土材料各向异性特征,基于摩尔库伦屈服准则,引入了节理连通率来反映结构面对岩体抗剪强度的影响程度。
(2)岩体材料的各向异性会造成岩体应力集中,按照材料各向同性进行开裂破坏量的计算存在较大误差。
(3)地下洞室的开挖量越大,考虑岩体材料的各向异性越重要,其对洞室岩体破坏量、应力、位移均有明显影响。考虑岩体各向异性后,洞周围岩破坏区体积增加约34%。
(4)与监测资料对比分析表明,考虑岩体材料各向异性来进行应力计算和屈服判别,其计算值与监测值更吻合,更能反映岩体变形真实情况。

