火灾工况下公路隧道通风智能控制模型研究
李 旭, 陈晓利, 李远哲, 张 磊
(1.广东省南粤交通仁新高速公路管理处, 广东 韶关 512600; 2.重庆交通大学 交通运输学院, 重庆 400074;3.招商局重庆交通科研设计院有限公司, 重庆 400067)
随着我国公路网不断向山区延伸,公路隧道在路线中占比越来越高,这大大增加了公路隧道运营中火灾险情发生的概率[1-2]。相较增加隧道设施防火等级的被动防火技术,对火灾工况下的公路隧道开展智能通风主动控制方法研究也非常重要[3-4]。
有关隧道火灾通风控制的研究,国外学者主要采用计算机数值模拟或者小规模模型试验的方法。李俊梅等[5]运用火灾仿真软件FDS对城市公路隧道进行模拟,研究了在阻塞工况下不同火灾规模的适宜通风速度。蔚艳庆等[6]在计算得到火灾工况下临界风速的基础上,运用FDS软件探索拥堵场景下4洞公路相邻隧道进行相反方向控烟通风的模式控制方法。郭庆华等[7]研究了火灾规模、隧道几何线形对最高温度与拱顶温度的影响。Huang等[8]为了解隧道入口封闭率对火灾行为的影响,采用CFD模拟了不同放热率、封闭率在0%~100%范围内的隧道火灾。高云骥等[9]通过建立1∶10缩尺寸竖井隧道模型,研究了不同火灾功率、发生位置及通风风速条件下,长隧道火灾排烟流动规律与隧道环境温度空间分布。王钟宽等[10]为探究不同坡度下隧道火灾的自熄现象,在缩尺寸模型中进行了甲醇燃料火灾试验,试验结果表明高坡度隧道由于烟囱效应较强,产生的纵向通风使得火源难以自熄。钟委等[11]探索了竖井结构隧道内,纵向通风对隧道排烟速度、隧道温度的影响。Li等[12]通过构建分岔隧道模型,研究了不同横向火源位置下隧道洞顶横向火焰长度和温度场分布。Jiang等[13]针对公路隧道的堵塞物火灾,对排烟层高度、排烟口下温度以及上下游速度进行了一系列的火灾试验研究。He等[14]研究了不同竖井高度和不同放热率下,竖井烟气的流动速度、烟气温升等特性。Zhang等[15]通过总结现有模型试验的数据,建立了包括火灾规模、通风速度和烟雾流动等7个关键参数的数据集,将机器学习应用于隧道火灾临界通风速度的预测。
现阶段,以机器学习为代表的人工智能技术快速迭代,为公路隧道烟气预测与控制带来新方法。张志刚等[16]基于随机森林理论,利用交通量、车速、风速等参数构建了公路隧道CO气体浓度预测模型。Hong等[17]提出了一种结合超级计算机和机器学习方法进行矿井巷道火灾烟气扩散的快速预测方法,研究结果表明随机森林和支持向量机模型对火灾烟气回流的预测性能最好,而人工神经网络模型对烟气回流长度的预测性能最好。
综上所述,公路隧道火灾通风控制研究通过数值模拟和模型试验的方法对隧道火灾烟气扩散规律、隧道温度分布特征、火灾工况通风控制等方面进行了深入研究。但现有隧道火灾通风控制方法还停留在基于有限工况条件下的经验公式推导或火灾现场人员的判断,难以实现控烟阶段隧道内合理纵向风速区间的精准把握,且实际火灾发生时刻的工况条件更加复杂多变,往往与先前假设的隧道火灾通风预案有差异,不利于实际火灾工况下对公路隧道通风进行及时、高效控制。
为此,本文以RBF神经网络作为回归算法,使用开源机器学习平台Tensorflow建立公路隧道火灾工况下智能通风控制模型。根据隧道车流量传感器获取实时交通量、隧道视频监控设备智能识别火灾发生位置与火灾规模,将经验公式计算出的风机开启台数作为训练样本,从而实现在真实隧道火灾发生时刻,根据隧道传感器的数据,自适应性的调整风机开启台数,以期减弱隧道火灾对人身财产安全的威胁。
1 神经网络模型原理
公路隧道在发生火灾时,为了减少火源产生的高温、烟气等不利因素对上游阻滞区域人员的影响,需要依照火源特性与受灾规模自适应生成隧道洞内各位置风机的控制策略,而RBF神经网络则可通过有限训练样本的学习,有效建立火灾工况下的风机控制模型。
1.1 RBF神经网络组成
RBF神经网络是20世纪80年代末提出的一种单隐层、以函数逼近为基础的前馈神经网络[18]。RBF网络能够逼近任意的非线性函数,可处理系统内难以解析的规律性,具有良好的泛化能力,且学习收敛速度很快,已成功应用于非线性函数逼近、时间序列分析、信息处理、系统建模、控制和故障诊断等领域[19]。
RBF神经网络的基础为RBF函数,它是某种沿径向对称的标量函数,定义为样本到数据原点之间径向距离(通常是欧氏距离)的单调函数,可表示为:

(1)
或表示为到任意一点A的径向距离的单调函数:

(2)
式中:a代表到任意一点A的欧式距离。为简化计算,本文运用高斯核函数作为RBF函数。
(3)
式中:x′为核函数中心;σ为函数的方差参数,控制了函数的径向作用范围。
RBF神经网络共有3层网络结构,包括输入层、隐藏层、输出层。输入层到隐藏层的神经元之间的权重全部为1。隐藏层是使用RBF函数作为激活函数的神经元。隐藏层与输出层之间为神经网络的连接关系,权重系数可通过训练而改变。RBF神经网络结构如图1所示。
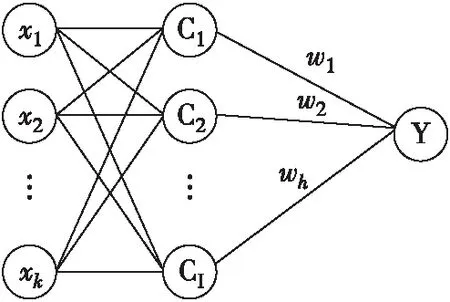
图1 RBF神经网络结构Fig.1 Neural network structure of RBF
1.2 RBF神经网络训练
RBF神经网络训练主要围绕3个参数的求解:基函数的中心、方差以及隐含层到输出层的权值。对于基函数中心xi,本文使用k-均值聚类算法,假设聚类中心有I个,设xi(n)(i=1,2,…,I)是第n次迭代时基函数的中心,则随机输入训练样本Xk,并寻找该样本最新的中心点,即
(4)
通过公式(4)不断迭代计算基函数的中心:
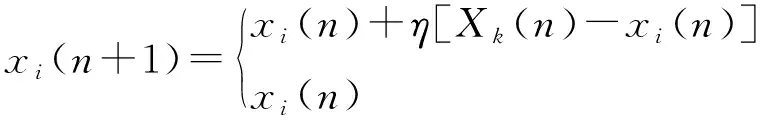
(5)
式中:η是学习步长,且0<η<1。
对于基函数的损失函数σ,由公式(5)求得:
(6)
式中:cmax为所选取中心点之间的最大距离;I为隐含层单元的个数。
对于隐含层到输出层的权值,则用最小二乘法直接计算得到,即对损失函数求解关于w的偏导数使其等于0,可化简得到计算公式为:
(7)
2 工程实例
2.1 工程概况
某隧道为一座上下行分离的双向4车道高速公路长隧道。该隧道右线进口平面线形为圆曲线,R=1 255 m,接缓和曲线,Ls=120 m,再接圆曲线出洞,R=700 m;左线进口平面线形为圆曲线,R=1 288 m,接缓和曲线,Ls=140 m,再接圆曲线出洞,R=720 m,隧道参数如表1所示。由于该隧道左、右线洞口除行车方向纵坡不同外,其余参数较为相似。为简化计算,本文所研究的火灾工况下,隧道通风控制均为隧道右线洞口。该隧道右线风机布设如图2所示,右线通风机选用No112型可逆射流风机,功率为37 kW,风速为34.0 m/s。
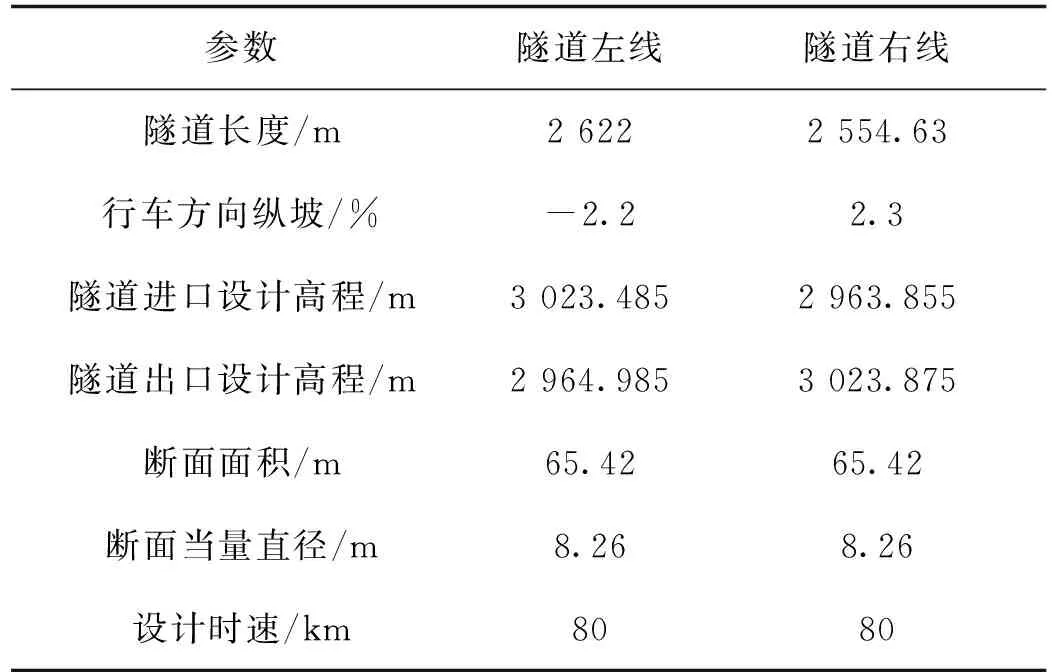
表1 隧道参数Table 1 A tunnel parameters

图2 隧道右线风机布设Fig.2 Fans layout of the right tunnel
2.2 火灾工况影响因素
该隧道线形复杂,在构建通风控制策略,尤其是火灾工况下通风方式的选择时,应综合考虑火灾规模、火源位置、交通条件、公路等级、隧道长度、自然通风、地形、海拔等影响因素。由于公路等级、隧道长度、自然通风、地形、海拔等因素是隧道固有特征,一旦建成,不因时间跨度而改变,故本文重点分析火灾规模、火源位置、交通条件等变量因素。
1) 火灾规模
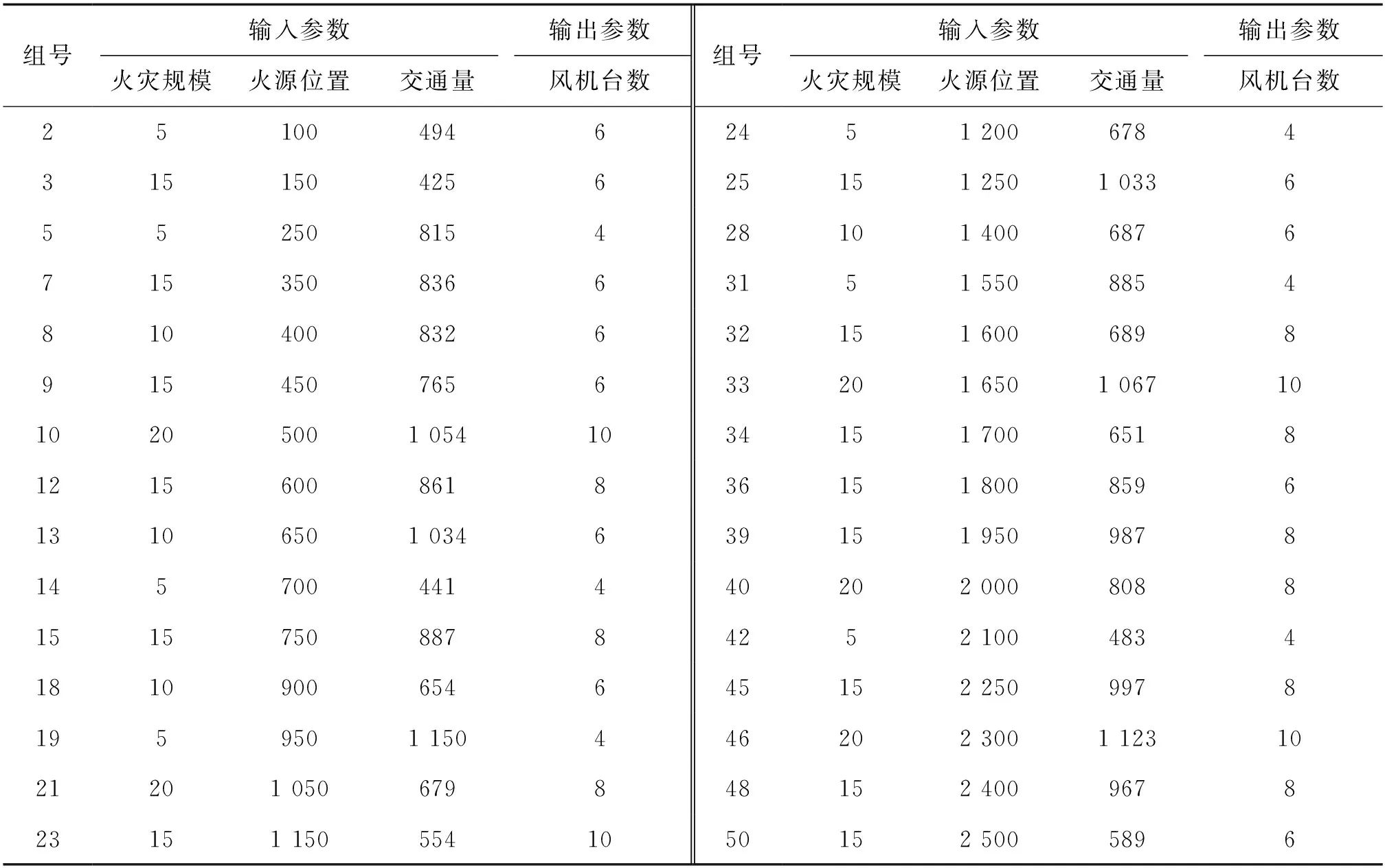
当公路隧道内发生自燃、交通事故等原因引发的火灾时,由于燃烧物与燃烧范围的不同,火灾的热释放率与烟气生成量也相应有所差异。因此,在制定通风控制方案时,首要考虑因素是火灾规模。根据《公路隧道通风设计细则》(JTG/T D70/02—2014)中关于公路隧道火灾最大热释放率的有关规定:对1 000 m 2) 火源位置 合理设置火灾区段划分,按不同区段设置相应的人员、车辆撤离路线和控制风机运转方案、烟气排出方案,以达到排烟灭火、人员逃生的目的。由于纵向通风隧道阻止火灾蔓延和烟雾扩散较为困难,故只能根据火灾时人员疏散组织进行隧道火灾区段划分,且隧道内火灾发生位置是随机的,为此将火灾发生位置定义为火源点距离右线进入洞口的长度。 3) 隧道交通量 隧道在发生火灾时,火源下游车辆可自行驶离疏散,而火源上游车辆受阻滞留,交通量由隧道内已滞留车辆与后续5 min内进入隧道内车辆构成,上游的2类阻滞车辆使隧道通风受阻,构成了隧道内局部阻力。根据该段隧道交通流量传感器获得过往交通量参数,由工可资料获得隧道路段预测交通量,高峰小时交通量按照日交通量的12%计算,则隧道右线历年交通量如表2所示。 表2 隧道右线历年交通量Table 2 Traffic volume of the right tunnel over the years 为保证火灾发生时火源处的烟气不向上游蔓延,危及车辆安全,要求隧道内必须保证具有最低的临界风速。其值的确定是根据火灾发生时,通过可燃物质的热释放率计算得到,计算公式如下[20]: (8) 式中:Vc代表临界风速,m/s;Cp代表恒压下空气的比热,kJ/(kg·K);ρ∞代表周围空气密度,kg/m3;g代表重力加速度,m/s2;H代表隧道断面净高,m;Q代表火灾热释放率,W;A代表隧道通风风道面积,m2;T∞代表环境温度,K;k为0.61,无量纲常数;kg代表坡度修正系数,由于隧道右线为上坡段,取值为1,无量纲常数。不同火灾规模对应的临界通风速度如表3所示。 表3 不同规模火灾临界风速Table 3 Critical wind speed of tunnel fires with different scales 当传感器检测到某隧道右线发生火灾时,随即进入火灾工况排烟工况,在忽略火风压与自然通风等次要因素的影响后,根据公路隧道通风设计细则的要求,隧道内排烟所需升压力计算公式[20]: Δp=Δpr+Δpm-Δpt (9) 式中:Δp代表所需风机总升压力,N/m2;Δpr代表隧道通风阻力,其由隧道内沿程摩擦阻力与局部阻力构成,由于火灾发生时上游车辆阻滞,因此阻滞的车辆也形成一部分的局部阻力;Δpt为交通通风力,在火灾下游车辆疏散出洞口后,交通通风力将下降为0。 以火灾规模、火源位置和隧道交通量等影响因素作为分类依据,通风控制参数为风机开启位置与风机开启台数,随机选取51组不同工况条件,并根据公式(9)计算得到51组通风控制数据,如表4所示。 表4 火灾工况下通风控制数据Table 4 Data of risk control system under fire condition 以火灾规模、火源位置、隧道交通量作为输入参数,将风机开启台数作为输出参数,利用RBF神经网络构建火灾工况下某隧道右线风机控制模型,从表4火灾工况下通风控制数据中随机获取30组参数作为神经网络训练数据,并将剩余21组数据作为检验组用于验证模型的精度与可泛化性,如表5所示。为了使各类输入与输出参数的量纲统一,在进行RBF神经网络训练前,需将以上4类参数进行归一化处理。 表5 RBF神经网络训练数据Table 5 Training data of RBF neural network 以火灾规模作为分组因子,在RBF神经网络风机控制模型的输入层变量有6个,通过计算并对比多组不同隐藏层变量的预测精度,最终确定隐藏层变量数为4,输出变量为归一化的风机开启台数。将30组训练数据代入到RBF神经网络中,并验证21组检验数据的精度,结果如表6所示,经验公式的计算值与RBF神经网络预测值的对比曲线如图3所示,经验公式的计算值与RBF神经网络预测值之间的误差分布如图4所示。 表6 RBF神经网络训练误差Table 6 Training error of RBF neural network 图3 计算值与RBF神经网络预测值对比曲线Fig.3 Comparison curve between calculated value and predicted value of RBF neural network 图4 计算值与RBF神经网络预测值误差分布Fig.4 Error distribution between the calculated value and the predicted value of RBF neural network 分析表6、图3、图4可知,训练组数据的相对误差为4.6%,检验组数据的相对误差为8.7%,均低于15%的精度阈值,RBF神经网络风机智能控制模型均表现出了良好的预测精度。 本文以某隧道右线工程为例,通过梳理影响火灾工况通风控制的影响因素,计算得到火灾工况下的风机控制数据,运用RBF神经网络进行训练和验证,获得了火灾工况下风机智能控制模型,得出以下结论: 1) 针对火灾工况下通风控制的影响因素,以火灾规模、火灾发生位置、隧道交通量3类主要变量因素,通过经验公式,获得51组随机火灾工况下的风机控制数据,并提取30组数据作为训练组,21组数据作为检验组,用于RBF神经网络的训练。 2) 通过对RBF神经网络的训练,风机开启台数预测误差逐渐下降到理想的范围之内,通过计算分配隐藏层到输出层的权重,自适应构建出火灾工况下风机开启台数智能控制模型,能提升控烟阶段隧道内合理轴向风速区间的精准把握。 3) 本文提出的风机智能控制模型选取的输入变量参数数据较少,随着隧道运营总时间的延长,计算参数的不断积累与获取,对该模型的持续训练,可进一步提高实际运营隧道的风机智能控制模型精度。
2.3 火灾临界风速
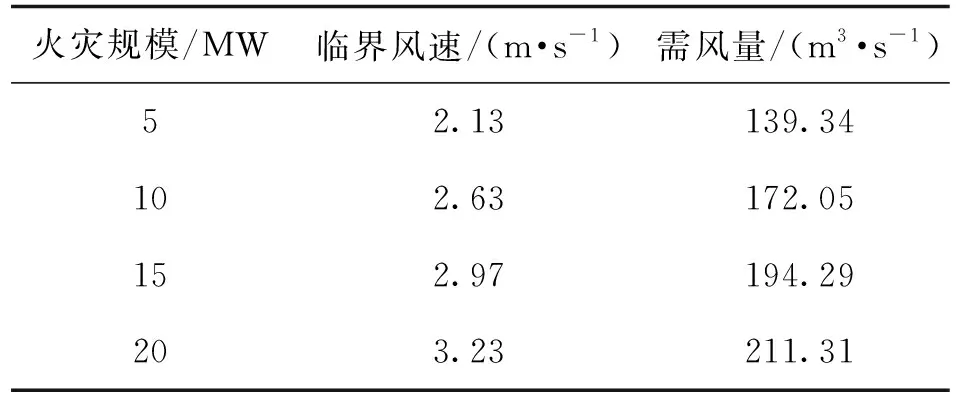
2.4 火灾工况风机控制数据

3 RBF神经网络风机智能控制模型
3.1 RBF神经网络训练数据
3.2 RBF神经网络设定与预测



4 结论

