销接式索夹几何参数精确计算方法研究
杨 洋, 曾瑞祥
(1.招商局重庆交通科研设计院有限公司, 重庆 400067; 2.中交第二航务工程局有限公司, 武汉 430040)
随着我国经济的快速发展,集交通功能与景观优美于一体的悬索桥建设需求日渐增加,空间缆索系统的自锚式悬索桥工程实例越来越多。主缆是悬索桥主要的承重构件[1],桥上荷载主要通过吊杆、索夹传递到主缆,索夹的设计、制作、安装对吊杆和主缆的运营工作状态产生直接影响。传统悬索桥索夹研究多集中于索夹的抗滑性、螺杆安装夹紧力、索夹安装位置等受力计算问题,而对空间索夹设计中的耳板中心夹角、安装倾角等空间几何问题研究的报道较少。
本文从非空间主缆悬索桥的索夹参数计算开始,推导空间主缆悬索桥索夹参数的计算方法,然后利用提出的计算方法,在考虑吊杆垂度因素情况下,计算索夹的设计参数。由于骑跨式索夹[2-3]对几何参数的容错能力较强,本文不再讨论骑跨式索夹几何参数的精确计算。
1 竖直面主缆索夹设计
竖直面主缆类型的悬索桥,主缆的斜率是通过结构总体计算找形获得,各个索夹位置受力平衡决定主缆的线形,吊杆的线形始终是按照竖直布置的。索夹耳板上吊杆销孔的位置,必须精确满足以上2个条件(即结构受力平衡和吊杆竖直),缆索系统才能准确维持成桥状态。
1.1 竖直面主缆索夹参数计算
耳板的吊索中心与主缆中心的连线,只要能处于竖直状态,就能保证吊杆处于理想的受拉状态,其连接部不受剪力,索夹立面如图1所示。

图1 索夹立面Fig.1 Elevation view of the cable clamp
吊索中心线与主缆垂直线的夹角α,是索夹加工的重要参数。α值为前端主缆倾角与后端主缆倾角的平均值,计算公式为:

(1)
式中:α前为前端主缆轴线与水平面的夹角;α后为后端主缆轴线与水平面的夹角。
设计中只要指定各个索夹的夹角α值,并进一步计算出销孔中心的局部坐标,即可指定索夹的几何参数。
1.2 索夹几何参数误差的危害
当夹角α误差过大时,吊杆的线形会偏离竖直线,甚至造成2根吊杆不平行,但其剪力会通过销轴释放。需要区别的是,单吊杆索夹只有一个销轴,变形协调能力更强,α角误差只会使理论索夹中心偏移,带来的危害要小于双吊杆索夹。
主缆和吊杆布置于竖直面内时,索夹的耳板也将处于竖直面内[3],如图2所示。但在施工中,索夹耳板也有可能偏离竖直面,造成吊杆销轴处产生面外的剪力,这种安装误差可能引起吊杆截面缺陷处发生疲劳断裂。
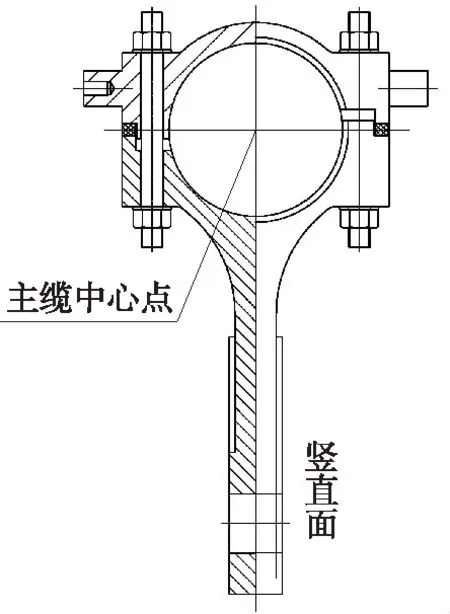
图2 索夹断面Fig.2 Section of the cable clamp
综上所述,竖直面主缆索夹的α角应精确加工,索夹耳板应竖直安装,结构才能符合成桥状态。
2 空间主缆索夹设计
2.1 工程概况
本文以某自锚悬索桥项目为依托,讨论空间主缆索夹参数的计算。该桥为35 m+130 m+130 m+35 m的独塔自锚悬索桥,其主缆的纵向布置为125 m+125 m,其横向布置在散索套位置距离桥轴线12 m,到塔顶处逐步渐变到0.3 m,如图3所示,为一典型塔顶收拢的空间主缆结构。

单位:cm图3 索夹平面布置示意Fig.3 Plane layout of the cable clamps
按照图4所示的索夹立面布置,从小里程侧向主塔方向,索夹编号是1到12号(12号索夹无吊杆),从主塔向大里程侧方向,索夹编号为12′到1′号(12′索夹无吊杆)。各个索夹在空间中的坐标,可根据桥梁结构总体计算得到。吊杆在梁上的锚固点,里程上与对应索夹的里程一致,横向位置与桥梁中心线的距离为12 m,竖向坐标0点在塔下梁顶面处。

单位:cm图4 索夹立面布置示意Fig.4 Elevation layout of the cable clamps
吊杆的空间布置,即是从索夹处主缆中心点连线到对应编号的主梁锚固点。索夹及耳板的构造参数,都要使该吊杆2点的连线为直线,不能有任何的角度弯折。
2.2 成桥状态的结构计算
采用Midas Civil建立该桥成桥状态有限元模型,如图5所示,其中主梁、主塔和辅助墩等结构构件采用三维梁单元模拟,主缆及吊杆采用只受拉单元模拟。
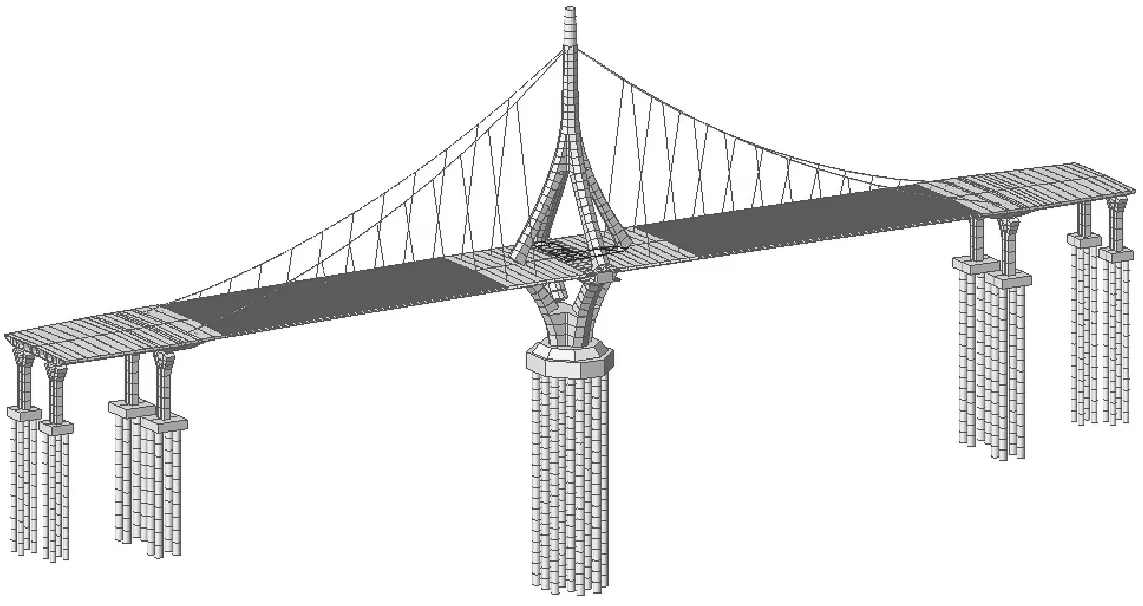
图5 成桥状态有限元模型Fig.5 Finite element model of the finished bridge state
在该模型基础上,对缆索、吊杆系统进行找形计算,得到表1中最终成桥状态的主缆空间坐标[4-6],作为索夹参数计算的基础数据。梁上锚点的坐标,采用设计坐标位置。表1中仅表达了单侧主缆、吊杆的情况,另一侧是关于Y坐标值0点对称布置。

表1 成桥状态各索夹中心和梁上锚固点空间坐标Table 1 Spatial coordinates of the center of each cable clamp and each anchorage point on the beam in the finished-bridge state
整个空间坐标系统的原点位置,设置在主塔里程处的主梁面中心点处。X值表达里程,主塔中心小里程方向为负,主塔中心大里程方向为正;Y值表达横向,顺X轴方向左侧为正,右侧为负;Z值表达高程,梁面以上为正,梁面以下为负,具体坐标轴方向如图6所示。
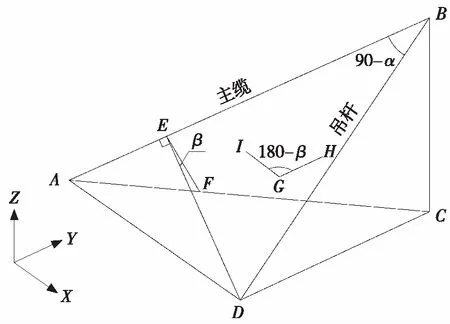
图6 主缆与吊杆的几何关系示意Fig.6 Geometric relationship of the main cables and hangers
2.3 空间主缆索夹参数计算
在图6中构建局部的主缆与吊杆的空间几何关系,AD线与X轴平行,AB线为主缆轴线,BD线为吊杆轴线,AC为AB主缆在水平面的投影,CD为BD吊杆在水平面的投影。索夹被安装在B点,∠ABD=90-α,计算出∠ABD即可计算出α角。
在索夹加工时,应考虑α角,并按照图1的示意,加工索夹耳板夹角。而安装索夹时,应把索夹耳板绕着成桥主缆轴线旋转β角[7],以便于吊杆指向梁上的下锚点,如图7所示。文献[8-9]都研究了自锚悬索桥主缆结构体系转换中,索夹的横向偏转角;文献[10]中研究了索夹在施工过程中的预偏角度确定方法,这类问题都是β角在施工过程中的变化问题。文献[11-13]着重研究了自锚悬索桥主缆结构体系转换中,主缆由竖直面空缆转向空间主缆的控制和施工方法。
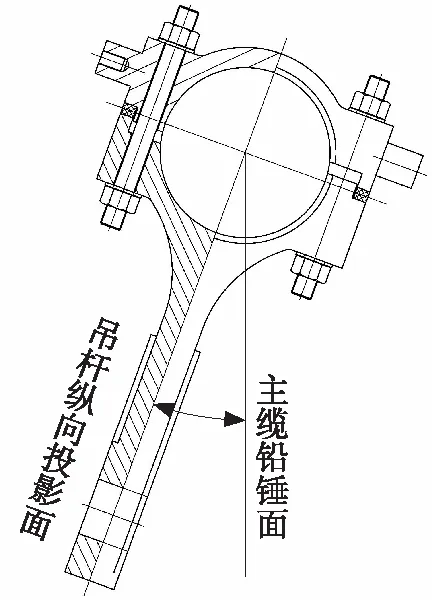
图7 索夹安装旋转角度示意Fig.7 Installation rotation angle diagram of the cable clamp
如图6中,ABC面是主缆竖直拉伸面,ABD面是吊杆纵向拉伸面,索夹安装时,应把耳板从ABC面内转入ABD面内,即要围绕主缆轴线转动β角。GH线是面ABC的法线,GI线是面ABD的法线,∠HGI=180-β,计算ABC面与ABD面的法线之间的夹角[14],就能计算出β角。
根据以上空间几何关系,推导出α角的公式为:
l1=ΔX主缆m1=ΔY主缆n1=ΔZ主缆
(2)
l2=ΔX吊杆m2=ΔY吊杆n2=ΔZ吊杆
(3)
(4)
其中,式(2)计算主缆向量,式(3)计算吊杆向量,式(4)计算2个空间直线的夹角,主缆和吊杆的向量用节点坐标差值计算。
根据以上空间几何关系,推导出β角的公式为:
k1ΔX主缆+ΔY主缆=0
(5)
k2ΔY吊杆+ΔZ吊杆=0
(6)
(7)
其中,式(5)根据节点坐标构建ABC面的方程,式(6)根据节点坐标构建ABD面的方程,式(7)计算2个空间面的法线夹角β[14],主缆和吊杆的向量用节点坐标差值计算。
式(2)~式(6)的计算方法,可作为悬索桥索夹参数的通用计算方法,既适用于空间主缆悬索桥,也适用于竖直面主缆悬索桥。该方法可以适应吊杆下锚点高程随路线中心高程变化,也能够避免索夹中心与吊杆下锚点的里程不一致带来的干扰。
2.4 考虑吊杆垂度的索夹参数
式(2)~式(4)中,吊杆均按直线处理,但如果吊杆较长,会有垂度效应,吊杆在索夹销轴处的空间角度应进行修正。
考虑垂度效应时[15],吊杆上端的斜率修正为KB,按下式计算:
(8)
式中:L为吊杆的水平投影长度;H为吊杆拉力的水平分量;ρ为吊杆的单位长自重;h为吊杆上下固定点的高差。
按照向量的定义,吊杆斜率与吊杆向量的关系为:
(9)
用式(8)计算出吊杆上端修正斜率KB后,带入式(9),即可计算出吊杆在ΔZ向量的修正值,再把修正后的ΔZ向量带入式(3)和式(6)重新计算。可理解为,考虑吊杆垂度后,吊杆上端变得更为陡峭,其ΔZ向量进一步增大。
由于索夹前、后的主缆在空间中有转角,因此在具体计算中,分别用前段主缆向量和后段主缆向量,分别计算出α和β值,然后再取平均值计算。索夹耳板加工的α值计算结果见表2,索夹安装耳板围绕主缆轴线旋转角度β值计算结果见表3。
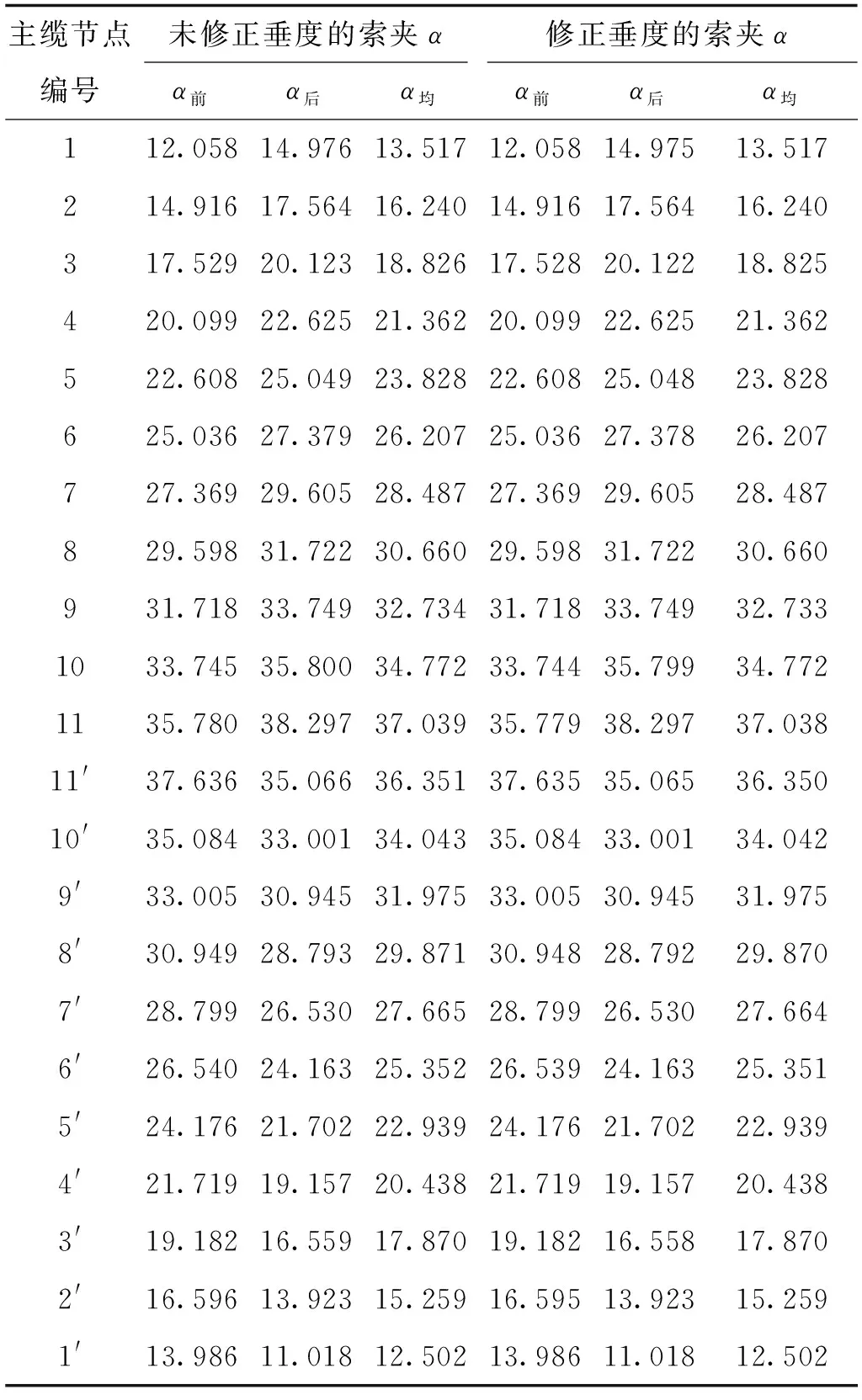
表2 成桥状态索夹α值计算结果Table 2 Calculation results of the cable clamp α in the finished-bridge state

表3 成桥状态索夹β值计算结果Table 3 Calculation results of the cable clamp β in the finished-bridge state
由表2计算结果可知,吊杆垂度修正,对索夹耳板加工的α参数影响很小,而且对长、短吊杆的影响没有显著差异。工程实践中,应根据吊杆长度的实际情况,判断是否需要修正吊杆垂度。
从表3计算结果可知,吊杆垂度修正,对索夹安装的β参数影响较大,且对长吊杆的影响较短吊杆更加显著,即在相似轴力情况下,长吊杆下垂更加明显,这一结论与工程实践相吻合。
经过CAD软件建模验证,未考虑吊杆垂度情况下,α角与β角的测量结果与计算的结果一致。
3 考虑荷载变化对索夹参数的影响
桥梁在实际运营阶段,梁上的移动荷载会发生变化,季节交替的温度变化也会引起缆索和主梁的长度发生变化。由于这些客观运营环境的变化,结构会变形调整到新的平衡状态,前述的主缆节点坐标会发生变化,吊杆的轴力也会相应变化,索夹耳板与吊杆会产生一定的转角,必须对该问题采取一定的措施,以防索夹与吊杆连接销轴的损坏。
3.1 平均值作为设计值
悬索桥是柔性结构,存在一定的几何非线性,不能采用线性荷载组合来处理移动荷载和温度变化对索夹的影响问题。应分别在最高温度和最低温度状态下,计算主梁满载、主梁空载、大里程跨满载小里程跨空载、小里程跨满载大里程跨空载工况的主缆坐标和吊杆轴力,每一工况都应该建立独立计算模型。针对各个工况计算α和β值,然后取α和β的平均值作为设计值。
3.2 使用球型关节销轴
吊杆连接销轴本身能释放吊杆面内的转动角度,即加工角α带来的误差。当吊杆在面外也有转角时,即安装角β带来的误差,连接销轴可通过球型关节设计来释放面外转动角度。球型关节转角参数,应大于(βmax-βmin)/2。
4 结论
1) 竖直面主缆索夹设计,只需考虑加工角α,安装角β始终等于0度,可以看成是空间主缆索夹设计的一种特殊情况,空间主缆索夹设计更具有通用性。设计及施工过程中,应控制索夹加工角α和安装角β的误差,以防吊杆疲劳损坏。
2) 空间主缆索夹的α角和β角设计,应采用空间向量几何的方法来求解。该方法可以适应吊杆下锚点高程随路线中心高程变化,也能够避免索夹中心点与吊杆下锚点的里程不一致带来的干扰。当吊杆长度较大时,按照空间向量关系计算的α角和β角值,应该考虑吊杆垂度影响,做进一步的修正。β角设计为绕成桥主缆轴线的转角,更加贴近实际施工,方便施工单位现场操作,减小安装误差。
3) 索夹参数的设计,还应考虑荷载变化带来的影响。

