图形坐标转换方法研究
葛巧莉
(南京图叶信息科技有限公司,江苏 南京 210046)
0.引言
随着测绘科学技术不断发展,我国在不同的历史阶段使用的坐标系是有区别的。关于在不同坐标系间的转换研究有很多,因此这方面的研究相当成熟,2000国家大地坐标系(CGCS 2000)的广泛使用使地形图在另一个坐标系统下的转换结果误差较小[1]。坐标转换通常有两种情况[2]:一种实际上就是相同的椭球下某一点在不同椭球基准坐标系间的转换;另一种实际上就是将相同椭球坐标中的某点的坐标转换为另一个坐标参考系统。不同类型的坐标之间的变换包括大地坐标分别与高斯平面坐标和空间直角坐标间的变换。国内外广泛采用相似变换法来实现不同坐标基准的变换[3]。该方法通过多次将图形上的每个点平移、缩小或放大、旋转对原始网络进行变换,最后遵循目标坐标系。限制网络的外形轮廓始终保持一定的不变,因此点之间位置的变化不会发生[4]。相似变换法就是通过选取的公共点的两套坐标值,找出两套坐标系统之间的关系,再通过选取的转换模型来实现坐标转换。
对于DWG文件的研究较少,本文研究DWG文件图形坐标的转换,详细探讨矢量图形坐标转换的原理,研究基于AutoCAD二次开发的DWG矢量图件坐标转换方法以及点、线、面等实体图件及块实体图件的转换思路。以实验区域DWG文件为例,研究矢量图形实体坐标转换方法,给实际应用提出合理可行的方案。研究城市测量中采用的各类坐标系的基准和原理,以及各类坐标系间相互转换的原理;分析DWG文件格式及其存储方式,研究DWG文件中点、线、面等实体图形文件的坐标转换方法。结合实际操作,实现DWG文件图件坐标转换。
1.平面坐标转换方法研究
1.1 坐标转换模型对比
1.1.1 七参数转换模型
要完成两个坐标系之间的改变,实现此目的最便捷的做法就是首先挑选出相配的转换模型,再使用共用的点的坐标值取得两个坐标系间转换模型的转换参数值[5],不同的转换模型求出来的转换参数是不同的[6]。使用七参数法的适用条件是,当进行测量的区域面积比较大或者测量区域的环境条件有着显著的不同,这时各个测区需要单独考虑,使用七参数转换模型以保证误差较小。
由于地球定向等问题,不同区域的转换参数存在差异,需要两个坐标系之间的共用的点的值,然后才能求出转换的参数值。公共点个数大于或等于三个时,方程有解,可采用七参数转换模型实现目的。转换式如式(1)所示:
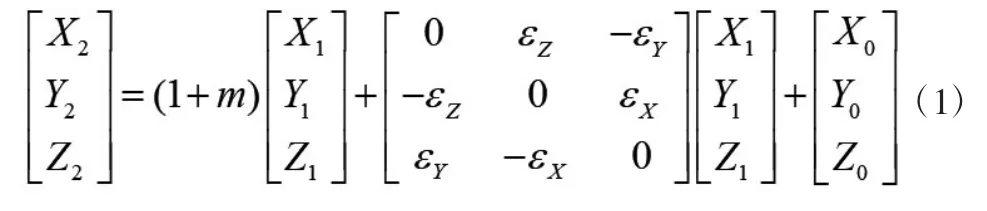
七参数模型转换的算法相比三参数模型转换的算法可以获得更高精度的结果。这些转换的参数值可以通过联测一些共用的点取得,能够直接获取这些共用的点在两个坐标系转换中的值并通过式(1)运算求得变化的参数值。
1.1.2 十参数转换模型
从坐标系转换的方面着手,剖析坐标系转换之间的变化,采用十参数模型。十参数法在有一定数量的共用的点的前提条件下,是一种误差较小的方法。
1.2 坐标转换精度分析
1.2.1 研究区概况
以研究区为例,区域中遍布点、线、单行文字、圆弧、填充等实体对象,数据成果经过验收,精度可靠,充分保证了本次坐标转换的参数求解和检核,精度非常高,完全满足工作需要的精度。
1.2.2 参数计算
(1)公共点的选取
公共点应该均匀布设于测量区域内,既要准确选取地物影像清楚的容易被发现的点,又要保证部分的绝对高程的差别较小。最好将点选择在道路交叉口,该位置的像控点局部高程变化小,且棱角分明。公共点分布示意图如图1所示。

图1 公共点分布示意图
(2)基于最小二乘平差计算模型参数
采用十参数模型,先选取公共点,运用小二乘法原理间接平差,精度不得超过0.03,这就是参数计算的内检核。将第二次选取的公共点,用计算好的参数带入十参数模型,求取与对应目标坐标间的误差,这是参数计算的外检核。十参数模型进行参数计算的方法步骤简单便捷并且误差、目标坐标差都很小。通过比较发现,七参数的误差要比十参数的误差大许多并且过程繁琐复杂,需要先进行投影反算,然后利用二维七参数模型平差计算七参数,再用已知的参数的模型进行坐标转换后进行投影换算,需要浪费许多精力和时间。
1.2.3 精度分析
判断坐标变换模型误差大小,可通过内检核和外检核两个步骤。假设有p个具有两套坐标的转换公共点,选取q个用作计算转换参数,则这个q点就是变换的已知高程的水准点,其余的共用的点将进行检验模型的误差大小。按照一般情况,求得的内检核的精度都很小,由此可以说明共用的点并没有发生明显的偏移。如果求得的值比较大,则表明发生了明显位移,这个时候就需要重新选择点了。
由表1、表2可知:内检核精度值均较小,符合精度要求,经十参数转换模型求得的误差值均在±0.08 mm以下,七参数模型求得的误差在±0.2 mm以下,所以十参数模型与七参数模型相比,误差更小,更为精准。坐标的变换过程终结后才会进行外部检核,它是根据转换模型的公式运算出两个坐标系间之差,用此数值来判定检核。

表1 十参数模型误差 单位:mm
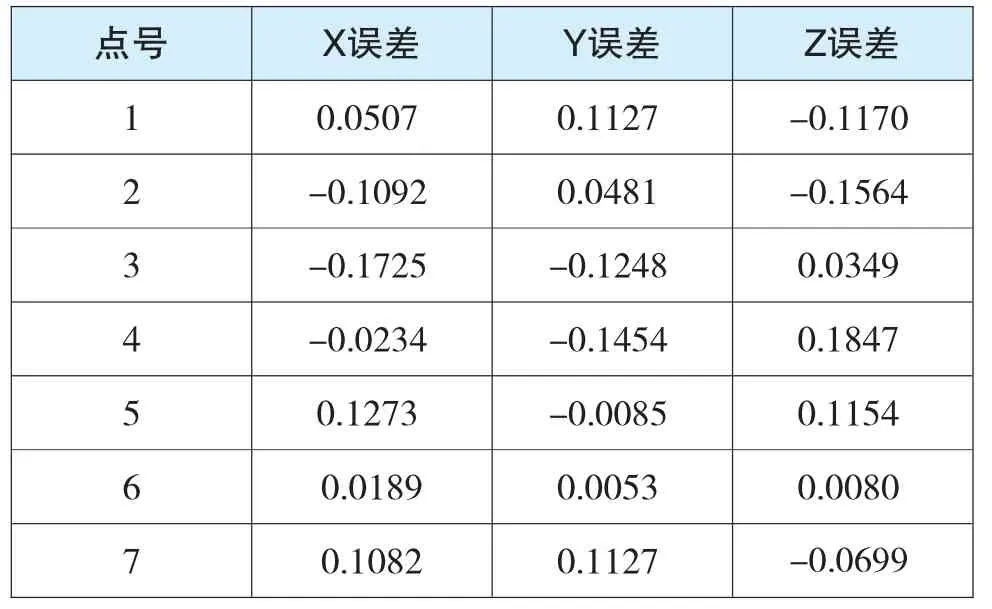
表2 七参数模型误差 单位:mm
由表3、表4可知:十参数模型转换求得的误差均在±0.03 mm以下,七参数转换模型求得的误差在±0.2 mm以下,十参数模型和七参数模型外检核误差均符合精度要求,但十参数的误差要比七参数的精准。所以内检核和外检核均符合精度限制。
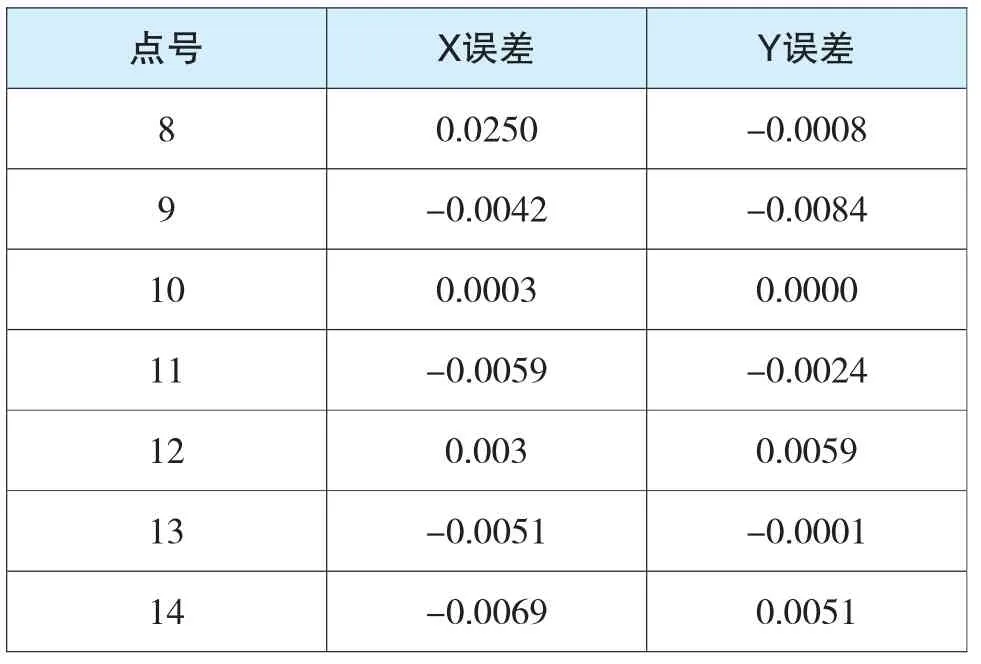
表3 十参数模型外检核误差 单位:mm

表4 七参数模型外检核误差 单位:mm
2.基于十参数模型的图形坐标文件转换研究
2.1 DWG
DWG格式文件的数据是二进制的,共有5种二进制的数据形式;DWG格式文件的数据结构也是由5部分组成。其中实体部保存着该文件中图形的全部实体。图形实体是AutoCAD中的基本图形单元,种类有许多,如点、线、圆、弧、块、尺寸标注等。
2.2 图形转换方法研究
传统的图形转换常采用整体转换法,其转换后误差较大,并且若将图形按照一定方式划分或将图形设置成块,转换后需要对图形的边缘要素进行相互衔接。现阶段,人们通常实行逐点转换法来进行图形转换。沿着路线对图形实体进行搜索,获得每个实体的节点的具体方位和属性信息,然后一个接一个地进行坐标转换,并将节点转换后的坐标值重新赋值给该点的具体位置和属性,从而更好地转换完图形中的所有实体。
2.3 转换精度分析
以研究区为例,选取图中的点、线等一般图形、单行文字、圆弧、填充进行图形转换。转换前的图形,图中包括点、线、单行文字、填充等图形文件中常见实体对象。转换后的图形,通过对比可发现点、线、单行文字、填充等实体对象的相对位置没有发生变化,图中的填充部分,转换后的边界线与填充部分也没有发生较大分离变化。
其中选取的14个点的转换精度如图2所示。
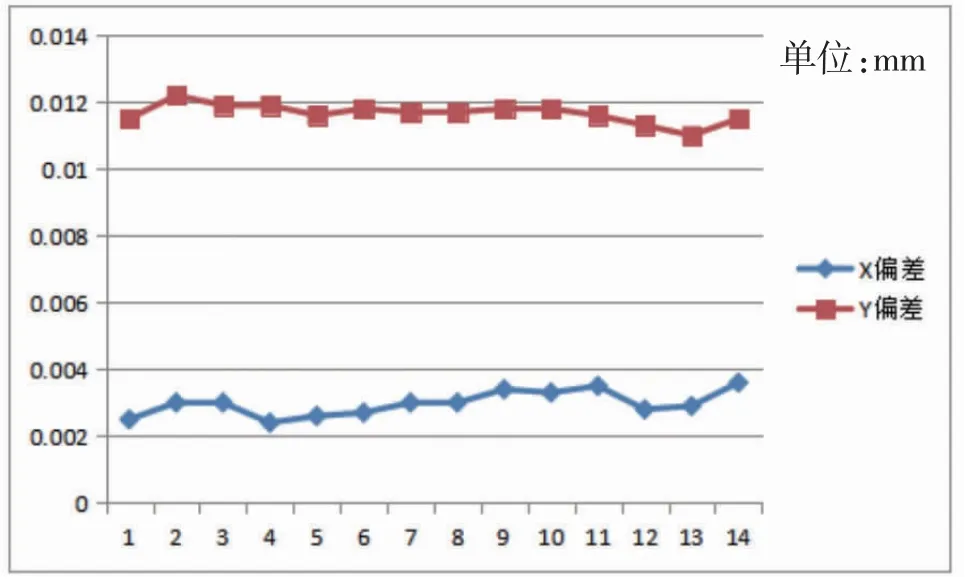
图2 图形变换精度
由图2可知:转换后的点都落在转换后的图上且图形转换的精度较高。X值的偏差均在0.003 mm以内,Y值的偏差在0.01 mm以内。X值的精度比Y值的精度高些。
选取研究区的圆弧,转换结果如图3、图4所示。
图3中有圆弧等实体对象,转换后的图如图4所示。通过对比可以发现,圆弧等实体对象转换前后的相对位置不发生变换。

图3 圆弧转换前

图4 圆弧转换后
由图5可知:转换后的点均落在转换后的圆弧上,精度也较高,X值的偏差均比Y值的偏差高些。X值的偏差均在0.003 mm以内,Y值的偏差均小于0.01 mm。图形转换的精度较高。

图5 圆弧变换前后的精度
3.结束语
为了充分利用不同坐标系下的测绘技术成果,以便能够做到资源共享,如何实现不同坐标系之间测绘技术性能的相互转换就显得很重要了。图形作为一项重要的测量数据,在进行转换后会出现残缺或偏差的现象,不利于正常使用。本文介绍了坐标转换的模型,DWG文件以及DWG文件的图形转换的成果,主要研究结论有以下几点:
(1)在平面坐标研究方面,通过比较七参数转换模型与十参数转换模型可知,十参数转换模型精度高、过程简便,而七参数转换模型精度一般、过程繁琐。
(2)采用逐点转换的方法对DWG图形文件中各实体对象转换,该方法只取决于转换参数的求取误差,不存在额外的精度损失。
——以大班艺术领域为例

