面向工程测量的自标定图像系统设计与精度测量研究
刘小云
(重庆市勘测院,重庆 400000)
0.引言
随着社会需求的发展,工程建设产业不断发展壮大,实地工程现场测量需求也在不断增多,但由于传统土木工程测量方式会受到较为明显的现场条件限制,因此容易在结构监测中出现失真现象[1-3]。如何在工程现场准确追踪结构应变、构件位移的同时,又能保障追踪测量方法的经济性、可实现性,一直以来都是工程建设方面临的难题,而数字图像测量则是应对这一难题的有效策略[4-6]。作为数字图像技术之一,自标定图像系统可以在无接触的情况下实现针对复杂结构巨型构造体的实时点对点监测和追踪、三维位移追踪以及全场应变测量,为工程建设现场精准测量提供了一条有效途径。本次研究将数字图像自标定技术应用到工程建设现场测量之中,通过实现高精度、无接触的全场测量,为现代大型工程建筑提供建筑结构应变监测支持,在解决工程测量实际问题的同时,也为工程安全和工程效率提供了保障。
1.面向工程测量的自标定图像系统设计与精度测量
1.1 基于散斑图的自标定图像系统设计
研究主要采用自标定图像系统进行工程测量,与传统三维图像相关方法相比,自标定图像系统不需要使用标定板进行标定,因此更容易满足远距离测量等范围测量需求。但同时自标定图像系统会受到现场环境、标定结果等因素的限制,造成精度损失,因此在工程测量中自标定图像系统的高精度设计是非常有必要的。针对现场工程测量行为,研究基于三维数字图像方法,采用散斑自标定方法对相机外部参数进行标定,从而得到物体的三维全场变形信息。三维数字图像测量以双目视觉原理为基础,采用两台摄像机并行的方式来模拟人眼双目视觉,即将摄像机摆放在不同位置来对空间同一场景进行成像。同时研究从数字类三维图像技术角度出发,在制定自标定策略时选择散斑策略作为主要相机参数标定策略,并通过该策略得到构造的通场三维应变数据。人体双目视觉信息的获取效果便是数字性三维图像技术的基础目标效果。在图像信息获取与处理过程中,需要对两台摄像机成像所形成的两幅图像中的对应点进行匹配,在匹配成功后,需要对图像中的相对点位之间存在的空间偏差进行计量,进而利用三维坐标来匹配立体空间场景内空间坐标信息。人体双眼视觉模拟原理,如图1所示。
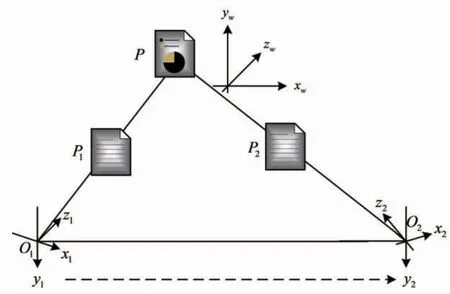
图1 人体双目视觉模拟原理
由图1可知:O1和O2为两个摄像机的光心,P(X,Y,Z)T为待测量的三维点,其通过两个摄像机成像的投影点P1(x1,y1)T和P2(x2,y2)T计算得到。数字图像相关的基本原理是通过对参考图像与目标图像之间互相对应的物理点进行匹配,进而得到三维全场变形信息。这是因为如果利用参考图像中的单位像素点来作为匹配基础,则很有可能无法在目标图像中获得唯一可得的对应点位。于参考图像中,将测量点作为中心点,此为中心针对(2 m+1)×(2 m+1)像素大小的方形块状区域进行抓取,同时在变形区间内对该区域的相对性区域位置进行追踪。
研究采用以反向组合技术为基础的高斯牛顿模型(In-verse Compositional Gauss-Newton,IC-GN)来实现快速准确地模板匹配,算法的最终目标是以相似性评估的方式对参考图像和目标图像的子区像素强度间的评估标准进行优化。在此过程中,采用最初数值估算的方法进行动态运算,最终选用单独的点位来对其所处的子区域进行迭代运算。研究从迭代得出的结果出发,估算邻近区域内的初值,并针对附近子区域的迭代结果数据进行计算,该步骤将会循环直至子区域的迭代传播完成。算法估算得到的初值需要能够保证IC-GN模型更快地进行高准确性收敛,同时对图像中相对较大的形变和旋转情况进行适配,相关函数选择零均值归一化最小平方距离函数,如式(1)所示:

式(1)中,g为运算目标子集合中的像素点(x,y)处的灰度数值;gm为运算目标子集合的强度运算平均数值;M为目标子集合的半宽度运算数值。使用二阶形状函数对两个摄像机中的变形图像子区进行匹配,如式(2)所示:

式(2)中,u(x,y)和v(x,y)为图像运算子区域中不同点在应力形变下形成的水平方向的位移变化和竖直方向的位移变化;u0和v0分别为图像运算子区域中心点位在应力形变下发生的水平方向的位移变化和竖直方向的位移变化;Δx为点位(x,y)到图像运算子区域中心点位的水平方向距离数值,Δy为点(x,y)到图像运算子区域中心点位的水平方向距离数值;ux、uy、vx和vy为图像运算子区域的第一阶段发生位移时形成的梯度数值;uxx、uxy、uyy、vxx、vxy和vyy为图像运算子区域的第二阶段发生位移时形成的梯度数值。在模型应用过程中,IC-GN模型首先对参考图像对应的参数进行提前计算,之后便不用再对其进行重新计算,参考图像子区的区域保持不变,在此情况下模型的计算效率有所提升,并且图像噪声不会对算法在噪声中产生的偏差造成显著影响。
1.2 自标定数字图像精度测量
相机进行自标定的精度对于空间三维重构和三维全场变形信息有着重要的作用,相机参数由相机内部参数和相机外部参数两个主要部分构成,其中相机内部参数主要由相机的中心点位、等效焦距以及相机畸变组成,而外部参数主要由世界坐标系与相机坐标系形成的矩阵参数和平移向量参数组成。在工程测量过程中,内部参数需要进行预标定,并且测量过程中保持不变;外部参数的值则会随着相机的相对位置而发生变化。在模型成像的理想环境和状态下,构造的图像坐标体系与空间坐标体系之间的相关性是可以用线性描述的方式进行描述的。摄像机成像过程中依赖的坐标系主要为四种环境坐标系:世界坐标系、相机坐标系、图像物理坐标系与图像像素坐标系。世界坐标系用Ow表达,它是外部世界环境下的物理坐标系,大多数时候摄像机与被测构造之间的三维坐标位置用该坐标系来表示,(xw,yw,zw)是其坐标值表达,坐标值在一般情况下采用公制单位进行度量;相机坐标系Oc是相机环境下的坐标系,其将光心作为坐标原点,并将(xc,yc,zc)作为描述该坐标系的坐标值,坐标值在一般情况下采用公制单位进行度量;图像像素坐标系将成像界面与光轴相交形成的中心点作为原点,并利用(x,y)来对整体坐标系内部的坐标值进行表达,坐标值在一般情况下采用公制单位进行度量;图像像素坐标系将成像图像阵列的左上角作为原点,(u,v)用来描述该坐标系的坐标值,坐标值的单位为像素。4个坐标系之间的空间关系,如图2所示。
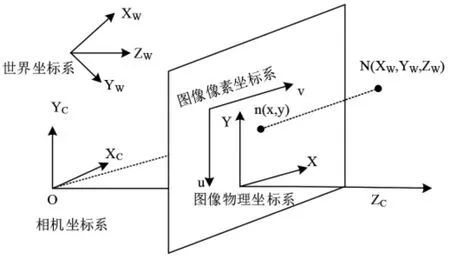
图2 四个坐标系之间的空间关系
预先标定相机内部参数,首先在固定的墙面上确定实验点,利用基于近景摄影测量的数码相机对三维坐标进行重新构建。调整数码相机的焦距直至能够清楚看到实验点,利用重构的实验点对数码相机的内部参数进行标定,标定后对其进行机械固定使内部参数保持不变,然后使用该内部参数固定的数码相机进行工程测量。在三维数字图像系统测量中,标定板很有可能无法与视场进行较为吻合的匹配,因此在进行大场景、远距离的测度时,标定板是无法近距离检测被测构造的。因此研究采用基于散斑的标定方法来确定相机的外部参数,并通过处理试件产生的数字图像信息来获取形变数据。此方法下试件的构造表面积需要存在一定的散斑图。也就是说,这些构造表面的随机灰度信息分布是承载一定形变信息的。在不对构造的力学特性造成显著影响的情况下,随机性散斑图会随着构造表面的变化发生一定程度的变化。在脱离标定板的情况下,散斑标定策略可以在复杂环境内保证标定的准确性,而且相机一旦安装完毕便可以立即投入使用,操作方便简单,同时降低了实验的人工成本,节省了大量实验时间。
2.面向工程测量的自标定图像系统精度测量结果分析
研究在进行自标定图像系统精度测量分析时,首先进行位移精度的实验:利用LSXPT隔振工作台来最小化振动引起的测量误差,并通过KSA400-11-X型位移台来实现精准平移。实验过程中研究搭建了字标数字图像和传统三维数字图像方法,并针对同一处表面散斑进行摄影,同时需要设置自标定摄影机的分辨率为2 400pixel×1 350 pixel。研究共设置两台相机,并同时配装200 mm焦距的佳能长焦镜头。对于普通三维DIC系统则设置2 048pixel×2 048pixel分辨率的相机,并配有50 mm的Kowa镜头。实验需要测量玻璃板的离面和面内位移,矩形区域为200 mm×110 mm,即所测量的区域,最后通过步进电机来加载精准位移。实验过程需要对精准位移台的位置进行变更,即模拟离面和面内的位移加载。自标定数字图像所用的相机与试件的距离为2.5 m,而三维数字图像系统与其的距离为0.5 m,期间采用通过LED照明。对于加载位移的设定,分别以1 mm和0.1 mm作为标准来进行,由于实验主要采用多组图像拍摄,因此最终以平均值作为结果进行比较。实验通过散斑定标和使用定标实现标定,利用PMLAB3D-DIC软件进行计算,最后比较测量精度间的差距。在面内位移加载实验部分,实验包括1 mm和0.1 mm两组实验,所得结果如图3所示。

图3 面内位移测量结果及相对误差
由图3可知:在面内位移为1 mm的实验中,自标定数字图像所得误差在0.3%左右,一般三维数字图像所得误差均小于0.2%,二者差距较小。在0.1 mm的面内位移实验中,一般三维数字系统误差在0.5%左右,而所提方法相对误差为0.7%左右,虽比前者略大,但绝对误差始终维持在0.1 mm以内。同时可以发现,随着初始位移加载逐渐减小,响度误差呈现出逐步增大的趋势,这是因为图像受到外部敏感度的影响,在平面位移较小时容易被随机噪音信号干扰。而自标定数字图像所对应的系统测量距离虽然远高于一般三维DIC方法,所得精度却与一般三维DIC方法基本相同,所以其实际上能够达到工程测量要求,同时受到环境条件限制更少。在利用同样的加载装置进行后续实验的条件下,实验通过对位移台位置进行变换来分析离面位移1 mm和0.1 mm下的加载实验情况,结果如图4所示。
由图4可知:与面内位移相比,两种方法离面位移所得误差均比其大。在加载位移为1mm时,三维DIC系统的误差维持在0.4%左右,在0.1mm时误差大约为0.6%。而自标定数字图像所得误差在1mm和0.1mm分别维持在0.6%和0.7%附近。同时两种方法在离面位移不大的情况下,所测量的误差均较大,说明两者均受到噪声和灵敏度制约。再进行应变精度的实验,此部分实验主要比较两种方法所得应变值,计算区域参数相同。在梁的纯弯段选择AB和CD两段进行分析,其中AB为垂直截面方向,CD则是水平方向。两种方法测得的AB和CD中各点x方向的应变情况如图5所示。

图4 离面位移测量结果及相对误差
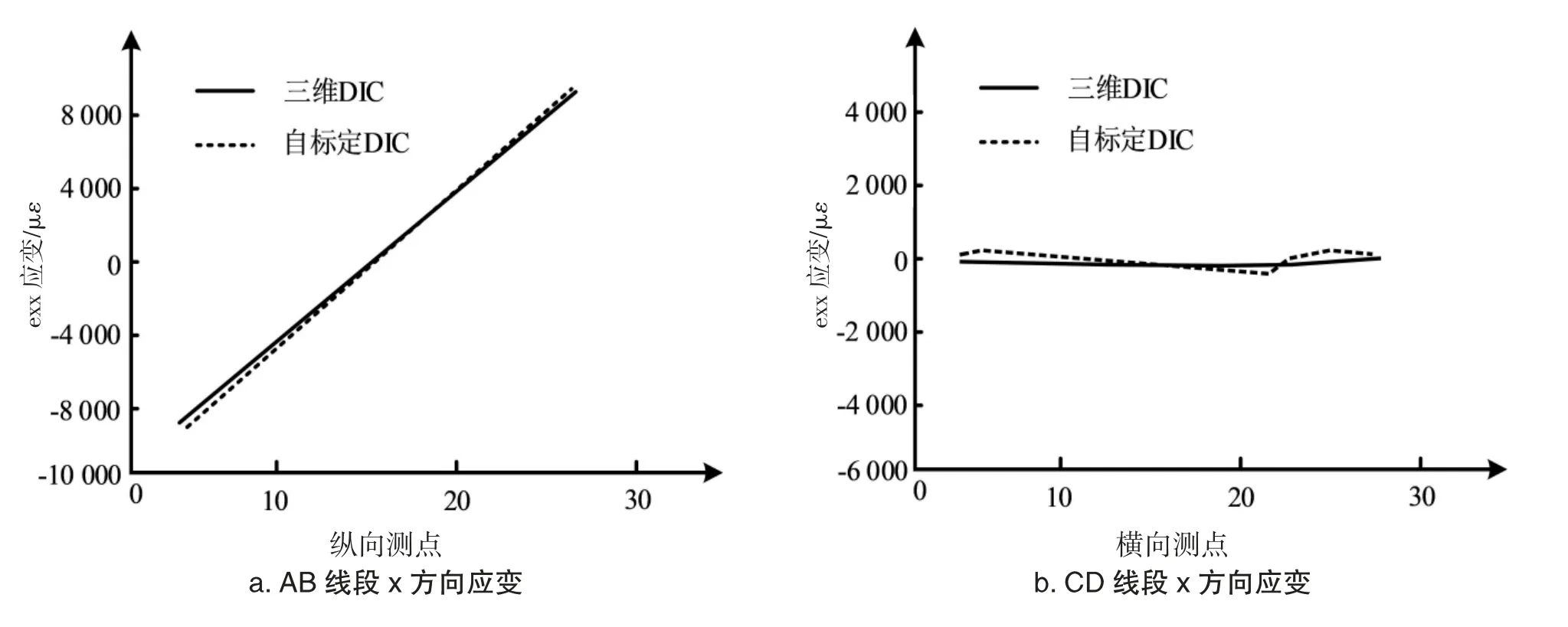
图5 各点X方向的应变情况
由图5(a)可知:AB段中两种方法所得应变值大约有4%的偏差,应变沿梁的高度整体保持线性分布状态。
由图5(b)可知:CD段两种方法所得应变值都保持在应变值0附近波动,并且相差范围维持在50 με以内,AB段与CD段的应变值均与梁的弯曲理论相符合。最后选择一块位于梁结构上下缘位置的区域,并采用两种不同的方法对区域内的应变状况进行测量,两种方法得到的平均应变状况如图6所示。

图6 平均应变状况对比
由图6可知:横坐标为加载次数,纵坐标是应变情况。两种方法的应变值曲线在走势上基本保持一致,相互间呈现不断靠近的趋势。而自标定数字方法由于受到远距离拍摄的影响,形成了扰动,因此得到的测量值出现了相对略大的波动。将其与应变片测量方法比较可以发现,在实验开始时,该方法所得结果与应变片方法在数值大小上具有高度的一致性。当变形量逐渐增大时,其所得结果的误差也相应增大,平均值是5.94%,原因是应变片本身导致的横向效应与两者区域未达到高度吻合。综上所述,所提出的自标定数字图像能够有效获取全场变形信息,其测量结果与应变片方法、三维DIC方法相比,偏差均较小,能够达到工程现场实验要求,同时研究设计的方法具有更大的测量范围,实用性更强。
3.结束语
为解决在实地工程测量中经常出现的由传统测量方式限制导致的测量失准问题,研究以三维数字图像方法为基础,设计自标定图像模型。模型采用IC-GN算法进行图像匹配,并在确定外部参数时采用散斑图自标定方法来保证系统的精度,最终通过实验验证的方式检验方法的应用效果。结果显示,在面内位移为1 mm的实验中,自标定数字图像所得误差在0.3%左右,同时在加载位移实验中,自标定数字图像在1 mm和0.1 mm尺度上的所得误差分别维持在0.6%和0.7%附近。由此可以看出,研究设计的方法较为精准,具有实用性,可以在工程现场的应变测量中得到精准的监测效果。

