基于模糊AGA-KPCA 的MIMU 传感器故障诊断方法
高运广,蔡艳平,盛 安
(1 湖南三一工业职业技术学院 工程机械学院,长沙 410129;2 火箭军工程大学 作战保障学院,西安 710025)
随着导航技术的发展和普及,微惯性测量单元(Micro Inertial Measurement Unit,MIMU)在导航领域中得到了广泛应用,MIMU 主要通过角速度和加速度传感器将测量信息传递给上位计算机,以此作为载体导航定位解算的基础数据[1]。受限于制造成本,一些中低端MIMU 传感器工作的可靠性不容易保障,因此有必要在应用时对MIMU 传感器的输出进行故障监测与诊断,以便及时发现故障并做出处理,从而为导航定位解算提供有效数据或发出警示。
目前,传感器的故障诊断主要有基于模型和基于数据驱动的方法。两者相比,数据驱动方法通常不需要建立精确的数学或物理模型,对专家知识依赖程度低,因此更适合工程应用。在基于数据驱动的方法中,主元分析(Principle Component Analysis,PCA)方法在传感器故障诊断中得到了广泛应用[2-5],但是PCA毕竟是一种线性处理方法,在处理非线性问题方面存在一定局限,而实际的系统通常又是非线性的。为了提高PCA 的适用性,有学者将非线性的核主元分析(Kernel Principal Component Analysis,KPCA)应用于传感器的故障诊断[6,7]。KPCA 中核函数参数的选择对模型性能有着重要影响,常规的选择方法大都根据经验人工选定,通常需要对参数反复调整,不仅操作繁琐,而且也难以保证得到最优值。
鉴于此,本文研究了一种应用于MIMU 传感器故障诊断的KPCA 方法,KPCA 核函数参数通过模糊自适应遗传算法(Adaptive Genetic Algorithm,AGA)进行自动优选,克服了常规选择方法中人为主观性强和操作繁琐的问题,提高了KPCA 的应用性能。
1 KPCA 原理
KPCA 通过非线性映射先把输入空间映射到一个特征空间,然后在特征空间中计算主元成分,这一非线性映射通过核函数来实现[8]。KPCA 对任一数据样本集x构造一个线性变换φ(xi),由此将x映射到高维空间,此时的协方差阵CF为:
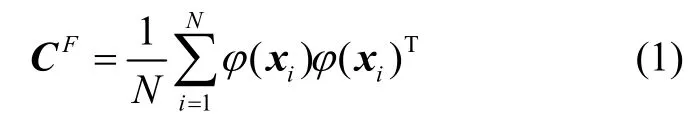
式中,xi为数据样本,N为样本个数。
通过求解特征方程:

得到特征值λ和特征向量v。
式(2)中C Fv可用下式表示:
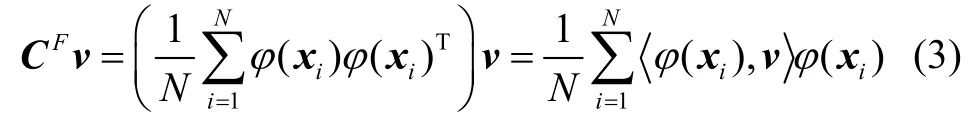
式(2)可等价于:
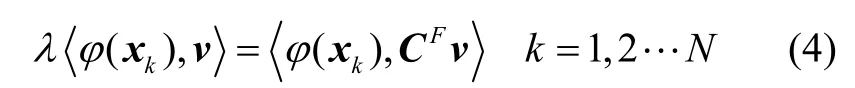
且存在系数a j(j=1,2…N),使
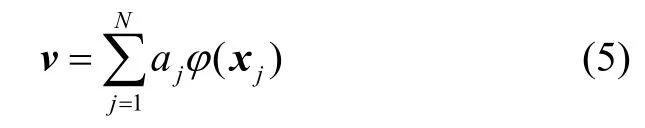
整理式(3)(4)(5)可得:

定义一个对称的核矩阵K,令矩阵元素K ij=φ(xi)Tφ(xj),1≤i≤N,1≤j≤N。于是式(6)可化简为:

式中,α为K的特征向量。由此可求得CF的特征向量v,进而可得到原始向量的主元成分:

2 模糊AGA
遗传算法是一种模仿生物进化机制的自适应搜索算法,具有强大的寻优能力[9-13]。将遗传算法应用于KPCA 核函数参数的自动优选,不仅可以提高参数选择的科学性,而且可以容易获得最优值。在标准遗传算法中,由于交叉概率pc和变异概率pm是固定的,由此可能导致算法不能收敛到全局最优。为此,不少学者对pc和pm自适应选取的问题进行了研究[14,15],这些方法大都利用平均适应度作为选择依据,但是平均适应度并不能真实反映个体适应度的一致程度,由此影响算法发挥最佳的性能。
为进一步提升遗传算法的性能,结合模糊理论能够模拟人类模糊逻辑思维和融合专家经验的优势[16],这里引入模糊推理对pc和pm进行选取。其设计思想为:将能反映一致程度的个体适应度标准差作为模糊推理系统输入;将pc和pm自适应计算中的调整参数作为系统输出。模糊推理系统设计如下:
(1)系统输入
系统输入变量为个体适应度的标准差,计算公式为:

式中,s为适应度标准差,fi为个体适应度,fa为群体平均适应度,N为种群规模。s的论域分为5 部分,分别为NB(负大)、NS(负小)、ZE(零)、PS(正小)、PB(正大),论域区间为[0,50]。
(2)系统输出
此处,pc和pm的计算公式如下:
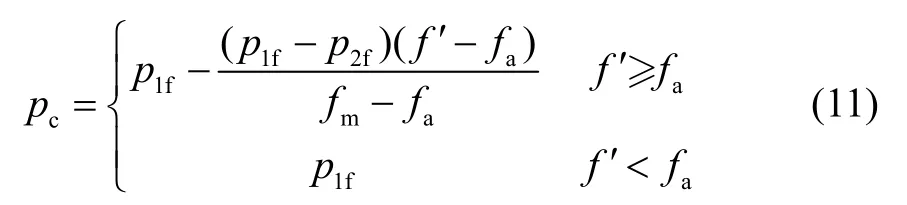

式中,fm为最大适应度,fa为平均适应度,f′为交叉个体中的较大适应度,p1f和p2f为pc的最大和最小值,p3f和p4f为pm的最大和最小值。p1f、p2f、p3f和p4f作为模糊推理系统的输出变量,其论域同样划分为5 部分,即NB、NS、ZE、PS和PB,论域区间根据pc和pm的取值范围选取,分别为[0.7,0.9]、[0.5,0.6]、[0.1,0.2]和[0.005,0.06]。
(3)推理规则设计
根据AGA 中交叉和变异概率的变化规律,模糊推理规则设计如下:

式中,pif为第i个输出变量,i=1,2 … 4。
(4)隶属度函数设计
系统隶属度函数采用三角形函数。对于输入变量s,隶属度函数设计如图1 所示。对于输出变量pif,根据不同的论域取值范围进行设计,以p1f为例,其隶属度函数设计如图2 所示。

图1 输入隶属度函数Fig.1 Input membership function

图2 输出隶属度函数Fig.2 Output membership function
3 MIMU 故障诊断
应用KPCA对MIMU传感器进行故障诊断的过程主要包括KPCA 建模、故障监测、故障定位和故障识别,故障诊断流程如图3 所示。

图3 故障诊断流程Fig.3 Flow of fault diagnosis
3.1 KPCA 建模
首先选取某型MIMU 的7 个传感器变量构建KPCA 模型,所取变量分别为3 个方向的角速度输出、3 个方向的加速度输出和1 个温度输出。取输出的200组数据作为学习样本,维数为7。在这些样本中,100组为MIMU 实测的正常数据,余下的100 组为故障仿真数据,包括传感器常见的偏差、漂移、精度等级下降和完全失效四种故障。KPCA 模型中的核函数参数通过模糊AGA 自动优选。
3.2 故障监测
通过KPCA 模型在特征空间计算Q统计量,即平方预测误差(Square Predicted Error,SPE),表示每次采样在变化趋势上与统计模型之间的误差,可度量外部数据的变化。此处将SPE 作为故障监测量:

式中,DSPE为SPE 计算值,φ(x)为非零特征值对应的主元和特征向量乘积之和,φ p(x)为前p个主元和特征向量乘积之和,化简后可得:
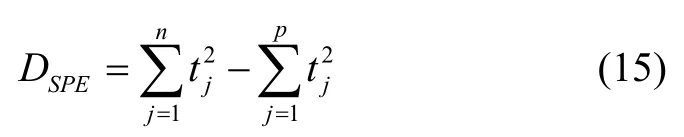
式中,t j为第j个主元;n为非零特征值的个数;p为主元数,可通过式(16)求出:

式中,λk为非零特征值。
SPE的监测限可根据其分布估计得出:

式中,Thα为监测限值,α为显著水平,g为SPE的权重参数,h为χ2分布的自由度。假设a和b是SPE的估计均值和方差,则g和h可由式(18)求出:

为了提高故障监测的可靠性,在计算SPE 前先对传感器数据进行平滑处理,计算公式如下:

式中,x k+i为传感器变量的测量数据;ω i为权重系数,且;q、r和M分别为设定的整数,S为数据个数,且q+r+1=M,k=q+1,q+2…S-r。此处,q取10,r取9,ωi取0.05。
3.3 故障定位
监测出故障后,需进一步定位故障。在PCA 方法中,发生故障的传感器变量和监测量之间存在一定的线性关系,但在KPCA 的非线性变换中并没有使用显式的非线性变换函数,而且核函数无法提供传感器变量和监测量之间的对应关系,因此PCA 的贡献图法不能直接用于KPCA 模型中故障传感器变量的识别。基于用传感器变量贡献量来识别故障的思想,为了完成KPCA 中传感器变量对故障的贡献量求解,此处定义第j个传感器的变量贡献量Conj,i为:
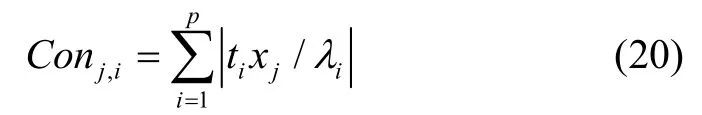
变量贡献量所占百分比PertT,j为:

变量贡献量变化ΔPertT,j为:

式中,ti和xj分别为第i个主元和第j个传感器变量;λi为第i个特征值;T表示时间,TF和T0分别为传感器发生和未发生故障的时刻;N为传感器个数。当监测出故障后,分析故障发生前后的ΔPertT,j,则可识别出故障传感器。如果某个ΔPertT,j最大,则可认定与此对应的传感器发生了故障,从而实现故障定位。
3.4 故障识别
通过故障定位可以找到发生故障的传感器,要进一步识别故障的类型,可通过如下故障模型进行判断:
(1)偏差故障

其中,es为系统测量误差,co为常数。
(2)漂移故障

其中,k为常数,Δtf为故障持续时间。
(3)精度等级下降故障

(4)完全失效故障
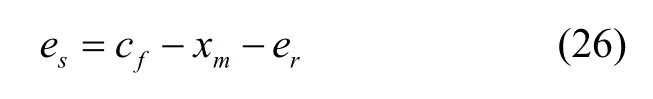
其中,cf为常数,xm为变量真实值,er为测量随机误差。
4 仿真试验
首先应用模糊AGA 对KPCA 的核函数宽度σ进行自动优选,求解步骤如下:
(1)编码
编码采用实数编码方式,取值范围为[0.01,10]。
(2)遗传操作
选择算子采用适应度比例方法,并采用最佳保留策略以提高算法执行效率。交叉算子采用算术交叉,变异算子采用非均匀一致变异,交叉和变异概率通过式(11)(12)自适应确定。
(3)适应度评价
KPCA 提取特征的主要目的是增强类的可分性,因此将类的可分性作为遗传算法适应度的评价准则。类的可分性通过类间散度矩阵Sb和类内散度矩阵Sw来衡量:Sb越大说明类间的差别越大,分类效果越好;Sw越小说明类内间的差别越小,类内聚类效果越好。根据这一准则,此处的适应度函数Fg为:

式中,

式中,L为类别数,Ci(i=1,2...L)为每类的几何中心,C0为所有类别的中心,X为数据向量。
(4)其它设定
初始群体采取随机方式生成,种群规模为60,遗传解算在执行到500 代时终止。
遗传解算过程中适应度的变化如图4 所示,求得σ=0.2837,根据式(16)得到主元数p=4。
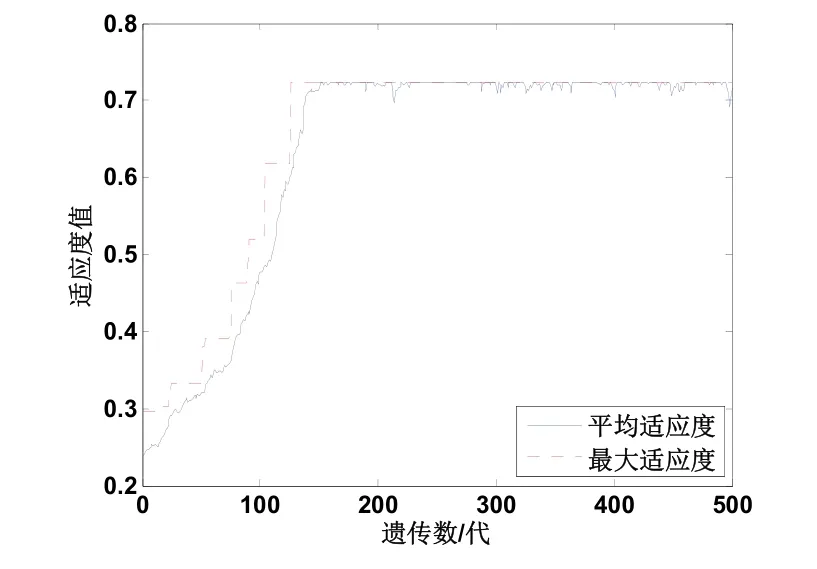
图4 适应度变化过程Fig.4 Process of fitness change for resolving
得到KPCA 优化模型后,取400 组MIMU 数据输入模型进行分析,其中前200 组数据为传感器正常数据,后200 组数据通过仿真对第一个传感器的数据引入偏差、漂移、精度等级下降和完全失效四种故障。
为了说明本文方法的优势,此处与人工选择核参数的常规KPCA 方法(参数σ取1)进行对比,两种方法的故障监测结果如图5 所示,监测限显著水平α取0.01。由图5 可见,本文方法均能很好地监测出四种故障;常规方法对故障的敏感程度不仅降低,而且存在一定程度的漏检。两种方法的故障监测结果对比如表1 所示,表1 中的准确率为准确识别正常(无误检)和检出故障个数之和与监测数据点总个数的比值。由表1 可得本文方法对四种故障监测的平均准确率比常规方法高出18.44%。

图5 故障监测结果Fig.5 Diagram of fault detection results

表1 两种方法故障监测结果对比Tab.1 Fault detection results of two methods
根据式(22)计算故障发生前后各传感器变量贡献的百分比变化,结果如图6 所示。由图6 可见,故障发生后第一个传感器变量贡献百分比变化最大,说明故障的部位均为第一个传感器,与实际完全相符,由此也说明了本文方法的有效性。
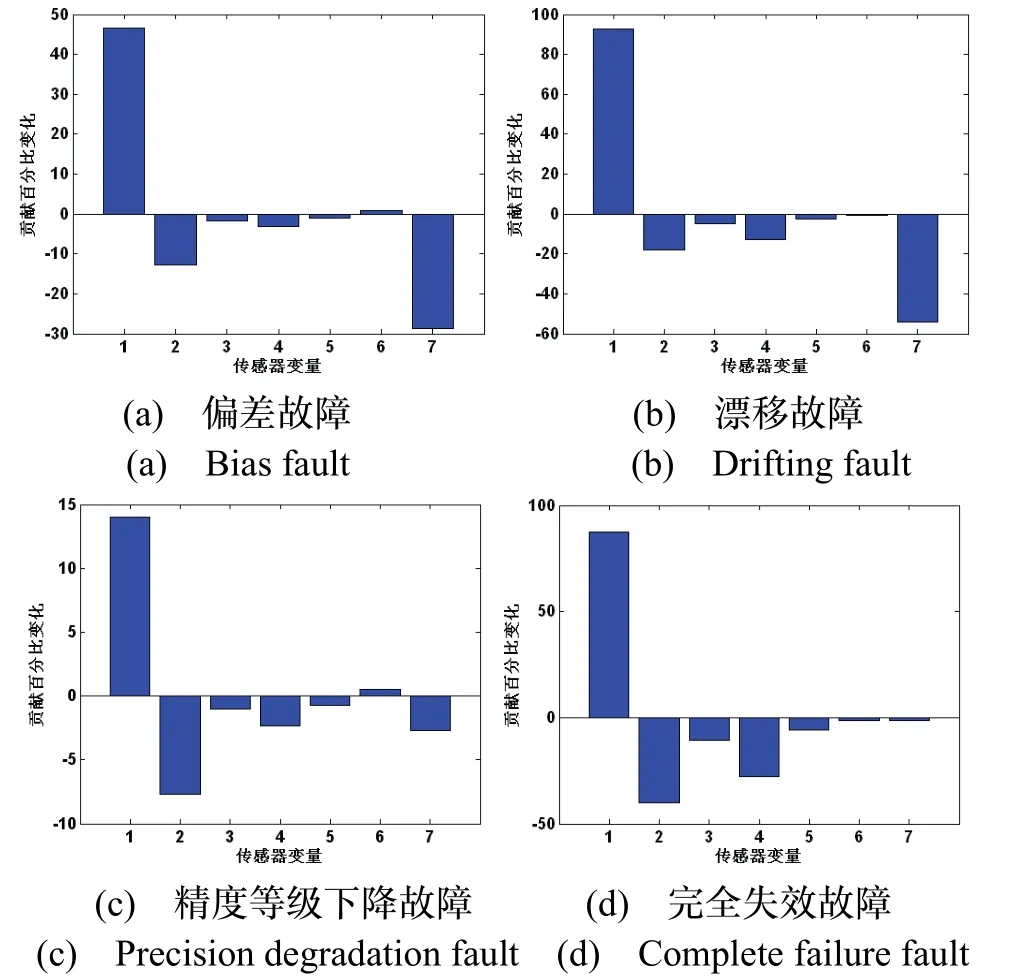
图6 故障量贡献百分比变化Fig.6 Diagram of contribution percentage change of faults
5 结论
作为一种数据驱动方法,PCA 在传感器故障诊断中得到了广泛应用,但它是一种线性模型,为了更好地适用于实际的非线性系统,本文提出了一种基于模糊AGA 的KPCA 非线性模型并应用于MIMU 传感器故障诊断。一方面,模型将SPE 作为故障监测量,利用传感器变量贡献百分比变化来定位故障;另一方面,为了提高KPCA 中核函数参数选择的科学性和减少建模工作量,采用模糊AGA 对核函数参数进行了自动优选。仿真试验结果表明,模糊AGA-KPCA 方法不仅可以有效地监测和识别MIMU 传感器故障,而且相比于常规的KPCA 方法更具有显著优势。

