一种基于回溯过程的里程计辅助SINS 初始对准方法
林宇森,缪玲娟,周志强
(北京理工大学 自动化学院,北京 100081)
捷联惯性导航系统(Strapdown Inertial Navigation System,SINS)是应用最广泛的导航系统之一[1]。由于越来越多的陆地车辆需要SINS 在行驶过程中完成初始对准,因此行进间对准已经成为了一个备受关注的问题。通常使用的外部导航传感器包括全球定位系统(Global Positioning System,GPS)、里程计(Odometer,OD)等,它们用来为SINS 的行进间对准提供辅助信息。GPS 的信号易受干扰,同时在掩蔽环境中无法使用。而OD 可以独立自主地测量车辆路程增量,以此为观测信息完成SINS 陆上对准。因此,陆用定位定向系统中使用基于OD 辅助的SINS 行进间初始对准,增强了陆用装备的战场适应性,引起了广泛的关注。
初始对准通常分为两个阶段,即粗对准阶段和精对准阶段。理想情况下,粗对准阶段提供初始姿态以使得SINS 在线性滤波模型下进行精对准。使用惯性参考系中的重力测量值计算初始姿态是一种有效的粗对准方法。文献[2]提出了一种TRIAD 算法,该算法使用两个不同时刻的矢量观测来计算姿态。为了充分利用测量值,文献[3]将粗对准问题转化为基于无限矢量观测的姿态确定问题,这种姿态确定问题被称为优化对准方法,通常通过q-method 方法解决这类问题[4]。惯性系解析对准方法可以进一步用于OD 辅助SINS的行进间对准。文献[5]结合惯性系解析对准方法提出了行进间粗对准方法,但该方法未进行载体即时位置的更新,在计算矢量观测时进行了大量近似。为了处理OD 固有的严重干扰,文献[6]加入了一个低通有限脉冲响应数字滤波器来衰减OD 中的干扰。为了补偿陀螺仪动态误差,文献[7]提出了一种基于卡尔曼滤波的OD 辅助SINS 粗对准方法。为了提高速度和加速度的跟踪能力,文献[8]中惯性元件和OD 在一个采样间隔内的输出采用直线拟合而不是假设成为常数。对于OD 辅助SINS 的行进间精对准,文献[9]提出了一种改进的ACKF/KF 的初始对准方法用于大失准角初始对准。上述研究的主要关注点是提高对准的最终精度,而对准的快速性也应是行进间对准中非常重要的评价指标。
近年来,随着导航计算机技术的发展,人们对回溯过程进行了研究,以提高短时间内初始对准的精度。为了解决在没有GPS 情况下的行进间对准的定位问题,文献[10]研究了一种基于回溯方案的OD 辅助行进间精对准方法(Optimization-Based Alignment,OBA)。在此基础上,文献[11]给出了一种基于回溯方案的大失准角OD 辅助行进间精对准方法。对于OD的异常值问题,文献[12]研究了一种用于OD 辅助SINS 的鲁棒行进间精对准方法。然而,上述对准方法仅将回溯过程用于精对准阶段,对粗对准阶段的回溯过程没有涉及。在粗对准和精对准中同时应用回溯过程对于快速高精度的初始对准更为有效。
本文提出了一种增加粗对准回溯的OD辅助SINS行进间对准方法,该方法可以快速自主地获得高精度的姿态和位置。所提出的行进间对准方法由粗对准和精对准组成。在粗对准阶段,结合包含即时位置更新的惯性系解析对准方案,提出了基于回溯过程的粗对准方法;然后利用粗对准的对准结果对卡尔曼滤波参数进行初始化,提出了基于回溯过程的精对准方法,进一步提高姿态和位置的精度。最后通过仿真试验证了所研究方法的有效性。
1 粗对准和精对准介绍
本文所使用的坐标系定义如下:
i:地心惯性系。其原点位于地心,zi轴沿地球自转方向,x i轴在赤道平面内指向春分点,y i轴与xi、zi轴构成右手坐标系。
e:地球坐标系。其原点位于地心,ze轴沿地球自转方向,xe轴在赤道平面内指向载体所在点的子午线,ye轴与xe、ze轴构成右手坐标系。
e0:将对准开始时刻的地球坐标系凝固后形成的惯性系。
n:导航坐标系(东-北-天)。
n0:将对准开始时刻的导航坐标系凝固后形成的惯性系。
b:载体坐标系(右-前-上)。
b0:将对准开始时刻的载体坐标系凝固后形成的惯性系。
1.1 改进的惯性系解析粗对准
1.1.1 姿态矩阵的分解
在惯性系解析粗对准中,姿态矩阵可以分解为:

其中,ω ie表示地球自转角速率,L0和λ0分别表示初始的纬度和经度,L和λ分别表示t时刻的纬度和经度,计算方法在1.1.3 节介绍。
1.1.2 惯性系解析粗对准
在n系下比力方程可以表示为[1]:

其中,

由式(16)可知,当α和β已知时,的求解已经转化为了Wahba 问题[13]。关于Wahba 问题的求解在文献[14]中有相应的细节,本文不再重复。
1.1.3 即时位置更新
对式(9)进行积分,可得位置增量如下:

1.2 卡尔曼滤波精对准
OD 辅助SINS 精对准的误差模型可以写为[15]
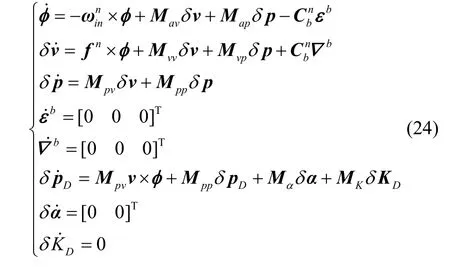
设置状态向量X如下:


2 基于回溯过程的粗对准和精对准
2.1 回溯过程
假设从位置A导航到位置B为前向过程,则从位置B回到位置A为逆向过程,将前向过程和逆向过程结合起来称为回溯过程。将回溯过程引入初始对准可以对测量数据进行多次处理,充分利用有限的信息,等效于延长了对准时间,从而提高对准精度[16]。
前向过程中SINS 的姿态和速度更新方程为:

假设SINS 的更新周期为Δt,式(36)(37)可离散化为:

逆向过程利用前向过程中存储的陀螺仪、加速度计和OD 的测量值进行逆向计算,得到逆向的姿态、速度和位置信息。由式(38)可得逆向过程的姿态更新方程:
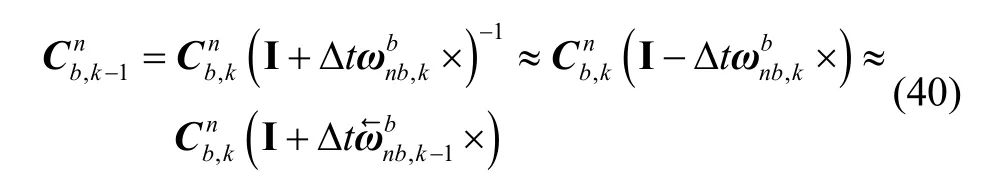
由式(39)可得逆向过程的速度更新方程为:
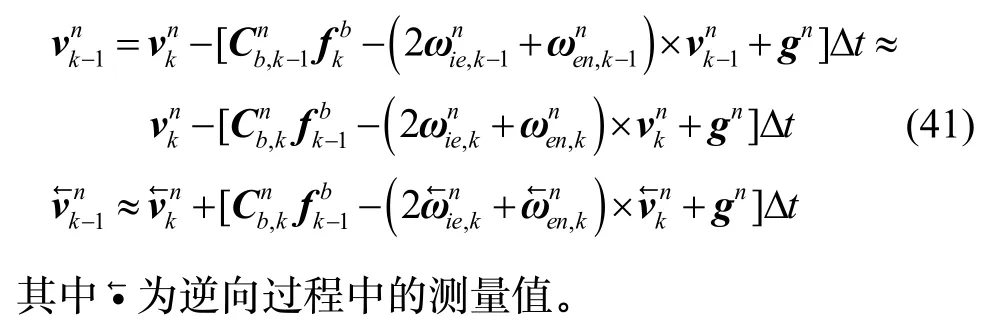
由式(40)(41)可知,逆向过程中测量数据的生成方式为:(1)将前向陀螺仪、加速度计和OD 的测量值逆序;(2)将陀螺仪与OD 的测量值和地球旋转速率的符号取负。在对准时间较短或测量数据较少的情况下,引入回溯过程可以人为地增加测量数据,等效延长对准时间。随着对准时间的增加,滤波器有充足的时间更容易收敛于稳态误差,从而提高初始对准精度。
2.2 基于回溯过程的粗对准
基于回溯过程的粗对准是在前向过程粗对准之后继续进行逆向过程粗对准。基于回溯过程的粗对准示意图如图1 所示,其中t1表示对准测量数据总时长。

图1 基于回溯过程的粗对准示意图Fig.1 Diagram of coarse alignment based on backtracking process
前向惯性系解析粗对准由式(1)和式(16)组成。而构成式(16)的矢量观测α和β如式(17)(18)所示。对于逆向惯性系解析粗对准,除了通过2.1 节的方法获得测量数据外,β的获取方式也与前向惯性系解析粗对准不同。
由式(17)可知,构成式(16)的矢量观测β表示b0系下的速度变化量。如果直接使用式(17)来计算逆向惯性系解析粗对准的矢量观测β,那么会缺少由前向惯性系解析粗对准到逆向惯性系解析粗对准转向时刻的速度变化,从而产生误差,因此需要利用OD 输出进行矢量观测修正。
在前向惯性系解析粗对准转向到逆向惯性系解析粗对准时,b0系下的速度由变为了,因此在逆向惯性系解析粗对准中,矢量观测β应修正为:

基于回溯过程的粗对准步骤如下:首先进行前向惯性系解析粗对准,由式(16)(17)(18)求得,通过式(1)求得;然后进行逆向过程测量数据的生成;最后进行逆向惯性系解析粗对准,由式(16)、式(18)和式(42)求得,通过式(1)求得。
相比于仅有前向的惯性系解析粗对准,基于回溯过程的粗对准增加了逆向惯性系解析粗对准阶段,延长了粗对准的时间。在初始对准时间较短的情况下,基于回溯过程的粗对准有利于提高粗对准精度。
2.3 基于回溯过程的精对准
为了实现快速高精度初始对准,将回溯过程引入到精对准之中。
由于粗对准结束后得到了对准开始时刻的姿态矩阵,因此精对准从对准开始时刻进行。基于回溯过程的精对准共进行了三个阶段:第一阶段是前向卡尔曼滤波精对准;第二阶段是逆向卡尔曼滤波精对准,所使用的是逆向过程的测量数据;第三阶段再次进行前向卡尔曼滤波精对准。
因此,整个初始对准过程包括两个部分:基于回溯过程的两阶段粗对准及基于回溯过程的三阶段精对准。初始对准的完整示意图如图2 所示。

图2 基于回溯过程的初始对准示意图Fig.2 Diagram of initial alignment based on backtracking process
前向粗对准过后,需要一定的时间延迟Δt用于计算逆向粗对准和三阶段精对准。对于现代导航计算机的强大计算能力,延迟时间很短。由于对准测量数据总时长t1远大于精对准计算所需时间,因此时间延迟Δt后,第二次前向卡尔曼滤波精对准可以实时输出当前时刻t2的姿态和位置,在精对准结束后可以立即转入导航阶段。
基于回溯过程的初始对准完整步骤如下:
(1)粗对准
①进行前向惯性系解析粗对准,同时记录陀螺仪、加速度计和OD 的测量数据作为前向数据;
②使用前向数据生成逆向过程数据;
③利用逆向过程数据进行逆向惯性系解析粗对准,并修正由回溯带来的矢量观测误差。
(2)精对准
①进行前向卡尔曼滤波精对准,速度和位置的状态初始值设置为已知的初始速度和位置;
②利用逆向过程数据进行逆向卡尔曼滤波精对准;
③再次进行前向卡尔曼滤波精对准,同时利用已知的初始速度和位置对估计量进行修正;
④当前向卡尔曼滤波精对准的回溯追赶上实时输入后,即满足导航状态的转换条件,可转入导航阶段。
3 仿真试验
3.1 仿真环境设置
通过仿真试验来评估所提出的初始对准方法的性能。设置SINS 中陀螺仪零偏为0.02°/h,陀螺仪随机游走为,加速度计偏值为100μg,加速度计随机游走为。设置OD 俯仰和方位安装误差角分别为15'和10',标度因数误差为0.005。设置对准开始时刻,前向粗对准的初始航向角误差为30°。
考虑到载体的转向与速度变化可以提高状态变量的可观测性,设计了车辆运动轨迹如图3 所示,车辆的姿态和速度如图4-5 所示,其中θ、γ和ψ分别表示车辆的俯仰角、横滚角和航向角;VE、VN和VU分别表示车辆的东向速度、北向速度和天向速度。车辆在对准开始时刻速度为零,开始对准后车辆立即行驶,对准时间共180s。车辆在90s 时航向角发生变化,变化幅度为5°。

图3 车辆的运动轨迹Fig.3 Trajectory of the vehicle

图4 车辆的运动姿态Fig.4 Attitude of the vehicle

图5 车辆的运动速度Fig.5 Velocity of the vehicle
3.2 不同行进间粗对准方法的比较
根据仿真得到的IMU 和OD 测量数据,使用惯性系解析粗对准方法(OBA)[10]和本文所提出基于回溯过程的粗对准方法(OBA Based on Backtracking Process,BOBA)进行粗对准。两种方法的姿态误差、速度误差和位置误差分别如图6-8 所示。图的左侧表示前向惯性系解析粗对准方法,即OBA 方法;图的右侧表示逆向惯性系解析粗对准方法,图的左侧和右侧共同构成BOBA 方法。两种方法结束时刻的姿态误差、速度误差和位置误差如表1 所示。

表1 不同行进间粗对准方法的对准结果Tab.1 Alignment results of different coarse alignment methods
由图6-8 可以看出,OBA 方法和BOBA 方法都可以完成行进间初始对准。这是由于两种方法都通过式(22)实现每一时刻的位置更新进而求取姿态,因此都适用于行进间的粗对准。而对于对准精度,无论姿态误差、速度误差和位置误差,BOBA 方法的误差均小于OBA 方法。这是由于在初始对准时间较短的情况下,OBA 方法的对准结果无法充分收敛,因此对准精度较低。而BOBA 方法使用相同的测量数据又进行了一个逆向过程粗对准,延长了一倍的对准时间,可以使对准结果继续收敛,因此对准精度高。

图6 两种方法的姿态误差Fig.6 Attitude error of the two methods

图7 两种方法的速度误差Fig.7 Velocity error of the two methods
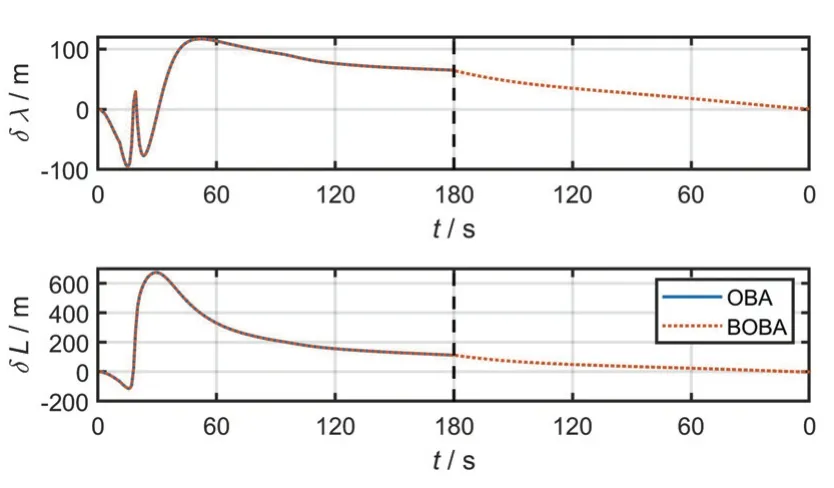
图8 两种方法的位置误差Fig.8 Position error of the two methods
表1 中BOBA 方法位置误差较小的原因在于经回溯过程粗对准后,OD 标度因数误差引起的前向位置误差与逆向位置误差相抵消,最终计算得到的位置接近初始时刻位置,因此位置误差较小。
3.3 不同行进间精对准方法的比较
根据仿真得到的IMU 和OD 测量数据,比较了传统的基于回溯过程的精对准方法(Kalman Filter Based on Backtracking Process,BKF)[10]和本文改进的基于回溯过程的精对准方法(Improved Kalman Filter Based on Backtracking Process,IBKF)。为了进一步提高精对准的精度,使用3.2 节得到的各自粗对准结果初始化两种方法的滤波参数。同时为了便于比较,省略了非常短的延迟时间Δt。图9 所示为两种方法OD 相关误差的估计与误差真值,包括OD 俯仰安装误差角、方位安装误差角和标度因数误差。两种方法的姿态误差、速度误差和位置误差如图10-12 所示,BKF 先从180s开始进行逆向卡尔曼滤波精对准,然后进行前向卡尔曼滤波精对准。IBKF 先由0 时刻开始进行前向卡尔曼滤波精对准,然后进行逆向卡尔曼滤波精对准和第二次前向卡尔曼滤波精对准。两种方法对准结束时刻的姿态误差、速度误差和位置误差如表2 所示。

图9 两种方法的OD 相关误差Fig.9 OD related error of the two methods

图10 两种方法的姿态误差Fig.10 Attitude error of the two methods

表2 不同行进间精对准方法的对准结果Tab.2 Alignment results of different fine alignment methods
由图9 可以看出,两种方法均可以估计出OD 相关误差,其中IBKF 的估计精度高于BKF。由图10–图12 可以看出,IBKF 的对准效果优于BKF。这主要是由于初始对准时间较短,BKF 的误差无法充分收敛,而IBKF 经过两次前向卡尔曼滤波和一次逆向卡尔曼滤波,延长了对准时间,使得误差曲线更为稳定,估计精度更高。在图11-12 中,曲线在0 时刻有瞬间的跳变,这主要是由于在逆向卡尔曼滤波转到前向卡尔曼滤波时,利用已知的初始速度和位置进行了状态修正,因此误差会有跳变。

图11 两种方法的速度误差Fig.11 Velocity error of the two methods

图12 两种方法的位置误差Fig.12 Position error of the two methods
同时由表2 可以看出,IBKF 的位置估计误差明显小于BKF。这主要是因为IBKF 首次精对准采用的是前向精对准,其初始速度和位置为精确的速度和位置。而BKF 首次精对准采用逆向精对准滤波,其初始速度和位置是由粗对准提供的,存在误差,因此BKF 的估计精度要低于IBKF。
综上所述,与现有的行进间粗对准和精对准方法相比,本文方法可以快速自主地获得精度更高的姿态和位置对准结果。相比于现有方法,所提方法航向角估计精度提高了45.1%,位置估计精度提高了58.1%。
4 结论
本文提出了一种高精度OD 辅助的SINS 行进间对准方法。通过将回溯过程引入到粗对准和精对准中,粗对准和精对准都获得了较高的对准精度。在粗对准中,通过改进的惯性系解析对准算法,减小了由位置变化引起的粗对准误差。同时,通过载体转向时矢量观测的修正,提高了回溯过程的精度。在精对准中,为了保证对准结果充分收敛以及对准过程的连续性,引入了两次前向精对准和一次逆向精对准,等效延长对准时间达到提高精对准估计精度的目的。仿真试验证明了所提出的行进间对准方法的正确性和有效性。相比于传统前向对准方法,在一定程度上可缩短对准时间,提高初始对准精度。在载体航向变化明显的机动条件下,本文方法有很好的应用前景。

