基于强度扫描上下文回环检测的激光雷达SLAM 算法
周治国,邸顺帆
(北京理工大学 集成电路与电子学院,北京 100081)
随着人工智能的不断发展,同步定位与建图(Simultaneous Localization And Mapping,SLAM)技术在机器人应用方面,如自动驾驶[1]、家用机器人[2]、仓库运输[3]等领域都占据着重要地位。激光雷达可直接获得测距信息且对环境变化更具鲁棒性,使得激光SLAM 在实践中被广泛应用。在SLAM 系统中,机器人姿态和轨迹的估计往往伴随着不可避免的误差漂移,从而导致定位失败。回环检测可以有效地实现误差漂移纠正,其对构建全局一致的地图至关重要[4]。
目前基于激光雷达的回环检测工作重点在于局部描述符和全局描述符的构建。局部描述符的构建首先找到一个关键点,再形成关键点的集合,并将这些局部关键点集合编码为直方图,形成局部描述符,如PFH描述符[5]、SHOT 描述符[6]、FPFH 描述符[7]等。另外,Bosse 等人还提出了一种基于概率投票方法的Gasalt3D 描述符[8],尽管该描述符实现了良好的匹配性能,但由于此描述符的高维度,使得计算效率较低。采用局部描述符进行回环检测通常需要提取关键点以及大规模的几何计算,而全局描述符描述整帧点云的特征,无需提取关键点或局部几何信息进行大量计算,因而具有更高的运行效率。GLARE 描述符[9]及其改进描述符[10]将点之间的几何关系编码为直方图,而不是搜索关键点并提取描述符;ESF 描述符[11]使用由形状函数生成的直方图;M2DP[12]由He 等人提出,将扫描的整个3D 点云投影到多个2D 平面,并提取了一个192 维度的全局描述符,该方法比之前的点云特征描述符显示出了更优的性能,其对噪声影响和分辨率变化更具鲁棒性。此外,SegMatch 回环检测[13]引入了基于点云片段的匹配算法,在局部和全局描述符之间提供了折中方案,在大规模、非结构环境也能可靠运行,但该方法所有点需转到全局坐标系中且需要训练。Kim 等人提出了扫描上下文[14]描述符,将3D 扫描的点云编码为矩阵,引入具有旋转不变性的描述子快速搜索,然而匹配精度不够高且会出现回环误判。
近期研究表明,利用点云强度信息可以提升描述符的性能,有效地进行位置识别[15,16]。Guo 等人[16]证明了不同位置的强度信息是独特的,并提出了一种新的局部描述符ISHOT,该描述符由几何和强度信息组成,采用类似于文献[8]中概率投票策略进行位置识别,此描述符在位置识别准确度方面优于仅利用几何信息的描述符,但计算代价大。之后,Wang 等人[17]提出了强度扫描上下文(Intensity Scan Context,ISC)描述符,集成了点云的几何和强度特征,该描述符比当前仅采用几何特征的描述符具有更高的识别精度,且采用两级分阶段位置识别策略,相较ISHOT 进行回环检测效率有所提升。在前端里程计部分,现有激光雷达SLAM解决方案多为点云帧与帧之间的匹配补偿点云失真,然而该方式需要不断迭代计算变换矩阵,增加了计算成本[18]。值得注意的是,现有3D 激光雷达频率均在10 Hz 及以上,点云的两个连续帧间隔时间极短,因此我们可以利用在短时间内角速度和线速度恒定,以预测运动并粗略校正畸变,后续再进行优化补偿。
本文提出一种基于ISC 回环检测的激光SLAM 算法,同时利用激光点云的几何和强度信息以提升算法的定位精度,并以两步法分阶段对点云进行畸变补偿以保证算法的运行速度。
1 系统概述
激光雷达SLAM算法框架包含前端激光里程计和后端回环检测,如图1 所示。前端包括:①点云预处理及运动畸变补偿。滤除无效点云及距离过远等不可靠点云,以恒速模型进行畸变补偿;②特征提取。计算点云曲率,提取线特征和平面特征并添加至局部特征图中;③位姿估计。接收线面特征,分别构建点到直线,点到平面的残差项,并求解旋转四元数和平移矩阵,估计机器人的运动;④点云强度信息校准及ISC特征提取。通过映射函数校准点云强度通道数值到[0,1]范围内,对非地面点进行几何和强度信息编码,生成ISC 特征图。后端包括:①回环检测。特征相似度计算分为两步,第一步计算其空间距离得分,第二步计算其强度距离得分,通过阈值判断回环是否发生,并发布回环信息;②后端优化:接收当前的线面特征、位姿估计和回环约束,构建因子图并进行全局一致性优化,得到优化后的位姿。最后生成最终轨迹和全局一致性地图。

图1 算法框架Fig.1 The framework of our algorithm
1.1 点云预处理及特征提取
多线机械激光雷达感知周围环境,是通过旋转M个垂直排列的激光束阵列扫描垂直平面,并同时获得M组读数,激光束阵列按顺时针或逆时针方向在扫描间隔内以恒速在水平面上旋转,进行激光测量[19]。对于机械激光雷达传感器模型,将激光雷达的第k次扫描帧用Pk表示,该帧中的每个点用表示,其中m∈[1,M],n∈[1,N]。
当前主流激光 SLAM 算法,如 LOAM 和LeGO-LOAM 等算法,通过迭代估计两次连续激光扫描之间的位姿变换,即帧与帧之间的匹配来校正运动失真,但迭代计算需要不断求解变换矩阵造成计算效率下降。由于大多数多线激光雷达都能够以10 Hz 以上的频率运行,两次连续的激光扫描帧之间的时间通常极短,文献[18]证明了在第一阶段以恒速运动模型非迭代地补偿运动失真、在第二阶段位姿估计后重新计算失真的方式可以实现同水平的定位精度,且计算成本显著下降。对于特征提取之前的运动畸变补偿,本文提出采用短时间内角速度和线速度恒定假设的方法估计位姿变换。将机器人在第k帧的位姿用4×4 的齐次变换矩阵Tk表示,两个连续帧k-1 和k之间的6自由度位姿变换通过式(1)计算:
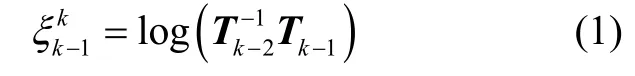
连续扫描帧间的位姿变换采用线性插值估计,帧间的短时间隔用δt表示,如式(2)所示:

其中,函数exp(ξ)将李代数转化为李群。
由于多线机械雷达获取的点云在水平方向上稠密、垂直方向上稀疏,因而水平方向上具有更丰富的特征且特征检测错误概率更小。因此关注点云的水平方向上并按照下式计算局部平面的粗糙度:

将第k帧点云Pk按式(1)(2)进行失真校准后得到非畸变点云,如式(4)所示。从而获得非畸变特征点云和,作为位姿估计模块的输入实现激光里程计估计。
1.2 强度校准及ISC 特征提取
激光雷达通过发射并接收激光束感知环境,强度通道可获得物体的表面反射率,因而强度信息可作为一种有效特征辅助激光里程计进行位置识别[20]。
考虑到强度通道读数不仅会受目标表面特性(如粗糙度、表面反射率)的影响,还受采集几何位置(如距离)、仪器性能(如透射能量)的影响[20],故必须对强度读数进行校准,以降低其他干扰因素带来的噪声影响。采用映射函数φ对强度通道读数ηr进行校准,如下式所示:

其中d为距离读数,映射函数φ反映了距离对接收能量的影响。由于回环检测中地面点对于位置识别通常没有贡献,本文在ISC 特征提取之前对输入点云首先采用高度为m的滤波器截取非地面点云。
将包含n个点的一帧点云表示为P={p1,p2...pn},激光点的强度值读数为η、空间坐标返回值为[x,y,z],所以每个点在局部笛卡尔坐标系下表示为pk={x k,y k,z k,ηk}。将每个点在x-y平面上转为极坐标,得到下式所示坐标形式:

将每帧点云按极坐标的环向和径向划分为N s×Nr的子空间[16]。每个子空间区域定义为Sij:
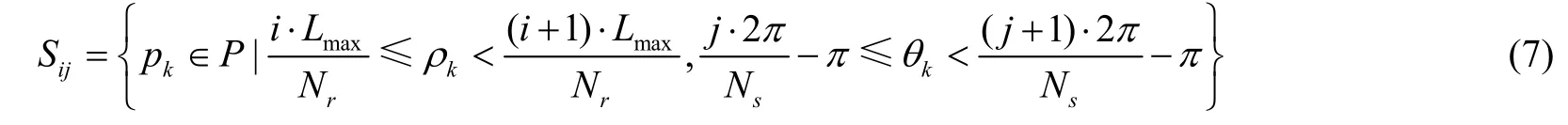
其中i∈{1,2...Ns},j∈{1,2...Nr},Lmax是为了去除距离较远的不可靠点云而设置的距离阈值。对于同一物体,返回的强度值读数通常是一致的,而划分的每个子空间中点云数量远小于一帧的点云总数,因此假设每个子空间中激光点强度值相同,定义如下:
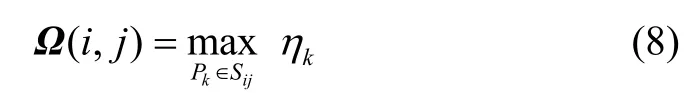
该全局描述符Ω本质是一个二维矩阵,包含环境中的几何信息和强度分布信息。
1.3 位姿估计及二次畸变补偿
对于每个线特征点pe∈,我们选取全局线特征地图中的近邻点云计算其协方差矩阵,当点都分布于一条线上时,协方差矩阵会有一个较大的特征值,与其对应的特征向量即被视为线的方向,近邻点云的几何中心被视为该线的位置。同理,对于每一个面特征点p s∈,可得到由其近邻点云构成的面位置为、面的法向量为。
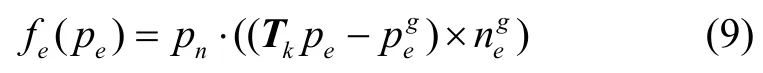
其中pn由式(10)得出:

面特征与全局地图的距离按式(11)求解:

传统算法特征匹配只优化上述几何距离而特征点的局部几何分布情况被忽略了。然而线特征和面特征在连续扫描中被一致地提取对于匹配而言是极其重要的,因此采用文献[18]提出的方法引入权重函数平衡匹配过程中线面特征的提取。为了节省计算成本,将先前定义的局部粗糙度再次使用,来确定权重函数。对于局部粗糙度为σe的线特征点pe和局部粗糙度为σs的面特征点ps,权重函数定义如式(12)所示。

其中Ek和Sk是第k帧点云的线特征和面特征,通过最小化点到线和点到面的加权和距离来估计新位姿,如式(13)所示。采用Gauss-Newton 法求解非线性方程可以推导得出最优位姿,应用具有左扰动的模型估计雅克比矩阵,如式(14)所示。

其中[Tk pk]×将点的四维描述{x,y,z,η}转为三维描述{x,y,z} 并取自身的反对称矩阵。由此可推导出线和面残差的雅克比矩阵,即式(15)。

对于线特征点的具体做法为取距离当前点最近的五个点,根据其特征向量方向取两个点pa和pb构造残差及雅克比矩阵;对于面特征点的具体做法为取距离当前的最近点五个点构成平面并将其归一化,之后构造残差及雅克比矩阵。
基于上述对应关系,求解非线性优化问题可以得到最佳位姿估计,之后使用该结果计算新的对应关系和里程计估计,通过迭代位姿优化直至收敛获得当前的位姿估计。
在非迭代畸变补偿的第二阶段,基于优化结果重新计算失真,同理式(1)和式(4),按下式计算:

重新计算得到的未失真线特征和面特征将分别更新全局线特征地图及全局面特征地图。
1.4 回环检测
回环检测的目标是将当前位置Pn与历史数据库D={P1,P2,...Pn-1}中先前访问位置相匹配。随着访问位置的不断增加,数据库的规模也不可避免地会增大,从而使计算成本增加。为降低计算成本,本文采用文献[17]提出的两阶段分层检索策略,利用快速二进制操作加速位置匹配过程。
第一阶段计算几何相似性进行快速重识别。对于一个给定的ISC 描述符Ω,它在局部坐标中的几何分布情况可以用二进制矩阵I表示,如式(17):

因此对于正在查询的ISC 描述符Ωq和候选ISC 描述符Ωc,可以获得他们的二进制变换矩阵Iq、Ic,推导得出其几何相似性的评估如式(18)所示,其中|X|为X中的元素总数,XOR(A,B)表示来自矩阵A和矩阵B的元素进行异或运算。
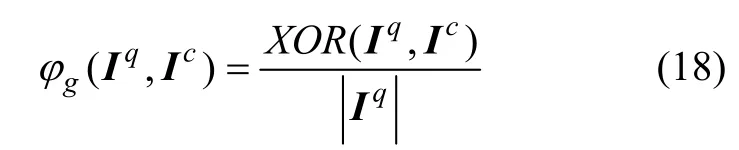
因为ISC 描述符中列向量代表着方位角,扫描帧的旋转体现为列向量的偏移[11],即位置识别中视角的变化体现为描述符列向量的偏移,因此为了满足旋转不变性,几何相似度按式(19)计算,

2 实验结果与分析
为验证本文所提出算法的先进性,分别在室外自动驾驶场景的公开数据集和室内采集数据中运行本文算法与LeGO-LOAM 算法[21]、LIO-SAM 算法[22],从定位精度、建图效果和运行效率三个方面进行对比分析;为验证本文提出非迭代两步畸变补偿法的有效性,设计了消融实验比较不同次畸变补偿的结果。
2.1 硬件平台与数据集
本文实验硬件平台为具有16GB RAM 的Intel Core i7-11700 和NVIDIA GeForce RTX 3070 的台式机,软件平台为Linux Ubuntu 18.04 下的机器人操作系统(ROS,Robot Operating System)。本文采用室外自动驾驶场景的公开数据集KITTI[23]中的00 和05 序列进行实验评估,采集平台如图2 所示,其中00 序列总距离约为3724 m,05 序列总距离约为2205 m。室内数据采集平台如图3(a)所示,采集环境如图3(b)所示,采集的走廊数据总距离约为140 m。

图2 KITTI 数据集采集平台Fig.2 Hardware platform for collecting KITTI dataset

图3 室内数据采集装置Fig.3 Device for collecting indoor dataset
2.2 定位精度分析
本节借助EVO 评估工具对SLAM 算法的定位精度进行评估,从轨迹可视化、绝对轨迹误差、相对位姿误差三个指标对比算法性能。
(1) KITTI 数据集
1) 轨迹可视化
本文提出算法与LeGO-LOAM 算法、LIO-SAM算法运行KITTI 数据集的轨迹可视化结果如图4 所示,其中图4(a)和(c)分别为00 序列投影在xy 平面上的可视化结果和xyz 三个方向上的输出轨迹,图4(c)(d)同理对应05 序列的可视化结果。观察图4(a)(c)可知本文提出算法在 00 序列上回环识别成功,而LeGO-LOAM 算法在最后回环失败,造成了轨迹漂移,而LIO-SAM 算法因对IMU 稳定性要求严格,而00序列初始部分IMU 数据输出不稳定导致运行失败;对于05 序列,三种算法均实现了回环识别,但从图4(b)(d)可以看出LeGO-LOAM 和LIO-SAM 算法在序列最后100 m 发生了漂移,与真值轨迹偏差增大,而本文提出算法直至序列结束都与真值轨迹保持着较小偏差。


图4 KITTI 序列轨迹可视化结果Fig.4 Trajectory results of KITTI sequences
2) 绝对轨迹误差(Absolute Trajectory Error,ATE)
假设算法估计位姿P1.....Pn∈SE(3),真实位姿Q1.....Qn∈SE(3),由于估计位姿和真实位姿通常不在同一坐标系中,通过最小二乘法计算从估计位姿到真实位姿的转换矩阵S∈SE(3)。第i帧的ATE 定义如下式所示:

本节ATE 指标评估同时选取平移部分进行误差分析,用均方根误差RMSE 统计,如式(23)所示。

表1 为三种算法在KITTI 数据集序列上的估计轨迹与真值轨迹比较得到的ATE 统计值。

表1 KITTI 序列的算法ATE 统计值Tab.1 Absolute trajectory error statistics on KITTI
图5 为三种算法的ATE 指标可视化结果。从表1中各项统计数值和图中曲线对比可看出,本文提出算法对KITTI 序列评估轨迹与真值轨迹误差更小,即算法精度更高,与LeGO-LOAM 算法相比,绝对轨迹精度提升56%(均方根值)。

图5 KITTI 序列的算法ATE 指标对比Fig.5 Absolute trajectory error on KITTI
3) 相对位姿误差
相对位姿误差(Relative Pose Error,RPE)比较姿态增量,描述的是相隔固定时间差Δ 两帧位姿差相比真实位姿的精度。第i帧的RPE 定义如下:

与ATE 相似,用均方根误差RMSE 统计此误差。
本节的RPE 指标评估仍同时选取平移部分进行误差分析。表2 为算法运行KITTI 序列上的估计轨迹与真值轨迹比较得到的RPE 统计值。图6 为RPE 指标的可视化结果。观察表2 中数据,本文提出算法的均方根误差(RMSE)统计值均为最小值,其他统计值本文算法误差最小的情况也占多数,整体而言本文提出算法性能更优。与LeGO-LOAM 算法相比,相对位姿精度平均提升约50%(均方根值)。

表2 KITTI 序列的算法RPE 统计值Tab.2 Relative pose error statistics on KITTI


图6 KITTI 序列的算法PRE 指标对比Fig.6 Relative pose error of algorithms
(2) 室内走廊数据
本文提出算法与LeGO-LOAM算法运行室内走廊数据得到的轨迹如图7 所示,由于室内走廊数据仅包含Lidar 传感器数据因而LIO-SAM 算法不参与测试。从图7 可视化结果可知室内短距离情况下两种算法在水平方向上精度相差不大,但本文提出算法在z 方向上输出轨迹更平滑,即高程误差更低。

图7 室内走廊数据轨迹可视化结果Fig.7 Trajectory results of indoor corridor dataset
2.3 建图效果与运行效率分析
表3 为三种算法运行相同KTITTI 序列的时间对比,其中 LeGO-LOAM 算法无回环检测模块,LIO-SAM 算法和本文提出算法带有回环检测模块。对于00 序列,本文提出算法运行时间最短;对于05 序列,本文提出算法相比LeGO-LOAM 算法,运行时间仅增加了0.42%。由此证明本文提出算法在增加回环检测模块的情况下,仍保证了运行效率。图8 所示为本文提出算法运行KITTI 05 序列的建图效果,轨迹起始点为(0,0),其中颜色过渡仅代表x方向距离变化。

表3 算法运行时间对比Tab.3 Algorithm time costs on KITTI

图8 本文提出算法建图效果Fig.8 Mapping result of our algorithm
2.4 点云畸变补偿有效性验证
我们利用KITTI 序列场景对比一次和两次畸变补偿的算法运行结果,以验证本文所采用非迭代两步法点云畸变补偿的有效性。
图9 展示了仅进行一次畸变补偿和进行两次畸变补偿的建图效果,从图9(a)可以看到进行一次畸变补偿后的算法虽然在平直道路上表现良好,但在拐角处出现了明显的漂移现象;观察图9(b)可知进行两次畸变补偿的算法在平直道路和拐角处的建图都很整齐,未发生明显漂移,算法鲁棒性有所提升。

图9 点云畸变补偿效果Fig.9 Effect of point cloud distortion compensation
为验证二次畸变补偿对于定位精度的提升作用,我们利用KTITTI 05 序列进行了消融实验研究,统计了不同畸变补偿次数算法的计算成本和定位精度。其中计算成本以里程计处理单帧点云的耗时衡量,定位精度以算法的绝对轨迹误差衡量,如表4 所示。对比实验结果,二次畸变补偿后计算成本增加了4.05%,轨迹误差减少了48.47%,由此验证了二次畸变补偿对于算法定位精度提升的有效性。

表4 不同畸变补偿算法的计算成本和定位精度对比Tab.4 Comparison of computational cost and localization accuracy in different distortion compensation algorithms
3 结论
本文提出了一种同时利用激光点云几何信息和强度信息的激光雷达SLAM 算法,在前端里程计通过线面特征匹配估计运动位姿,在后端回环检测以ISC 作为全局描述符进行回环识别以优化位姿,最终生成估计轨迹和全局地图。该算法的优势包含以下两方面:一是采用ISC 作为全局描述符,集成了点云的几何和强度特征,在回环检测阶段首先进行快速地几何结构匹配来筛选候选帧,再对达到阈值的候选帧进行强度结构匹配,最终发布回环信息到后端优化模块,从而实现高精度的位置识别;二是采用非迭代方式进行失真补偿,初始位姿对齐以短时间内的线速度和角速度恒定来估计运动,在位姿估计环节后重新计算失真并将补偿后的特征点云更新至点云地图,以此提高收敛速度,从而实现实时的定位与建图。
实验证明,本文提出算法在位姿精度上相比仅利用点云几何信息的SLAM 算法平均提升约50%,同时对比不包含回环检测模块的SLAM算法运行时间最多增加了0.42%,保证了运行效率。本文算法测试场景均处相对静态的环境中,并未考虑动态物体过多的场景,该类场景可能会带来位姿估计的严重漂移,之后的工作将集中于动态物体较多场景下对于算法定位精度稳健性的提升,以提高算法在实际工程场景中的适用性。

