一种动态分组的多节点协同定位编队构型优化方法

李清华，高 影，王振桓，王国庆，耿子成

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001）

随着无人机和无人驾驶车辆自主控制的发展，高精度的定位对于无人机集群和车辆协作至关重要。目前机载和车载导航主要依靠卫星和惯性导航系统，由于前者在复杂电磁、城市峡谷和其他全球卫星导航系统（Global Navigation Satellite System，GNSS）等受阻环境下容易受到干扰，后者则存在误差累积问题。针对以上问题，定位节点间通过信息共享来提供更高定位精度的协同导航技术受到越来越多的关注[1,2]。

国内外学者对多节点协同导航进行了针对性的研究。文献[3]和文献[4]提出利用卡尔曼滤波原理应用测距信息建立一个多行人协同导航系统模型的协同定位方法，抑制了在卫星受阻情况下惯性导航误差的发散，从而提高整体行人的导航精度。文献[5]提出了一种基于因子图优化的无人机集群协同导航方法，结合无人机之间的超宽带（Ultra Wide Band，UWB）测距信息为每架无人机构建局部因子图，将无人机集群的位置精度提升了3 倍，但是该方法并未考虑无人机集群编队构型对协同导航的影响。文献[6]提出了基于Cramer-Rao 不等式的水下机器人（Autonomous Underwater Vehicle，AUV）协同定位编队构型评价函数，分别确定了规则模式和线性模式下的最佳编队构型。文献[7]提出信息熵算法进行协同测量信息的评估，并选择最佳量测信息以减少低质量量测信息对多自主协同导航的影响，提高AUV 的协同定位精度。文献[8]提出了采用自适应粒子群优化算法和遗传算法相结合的混和元启发式算法，可以在线预测声波测距误差进而修正测量值，提高协同定位系统的精度和稳定性。文献[9]提出了一种与遗传算法相结合的K-Means 算法，通过扩展遗传交叉算法和变异算法有效地提高了遗传算法的收敛性，实现了多船智能协同控制的最优运动策略。

以上方法有效提高了单体定位性能，但仍存在以下不足：（1）未讨论协同系统节点较多时如何进行编队分组问题；（2）未讨论非编队控制下，自由运动的多节点协同定位时编队构型评价问题；（3）未针对测距限制等约束信息，对遗传算法求解的计算效率进行优化。

针对以上存在的问题，本文提出了一种基于改进遗传算法的多节点协同定位过程中编队构型实时优化算法。首先以节点间距离为量测信息，建立基于容积卡尔曼滤波（Cubature Kalman Filter,CKF）多节点协同导航模型；然后基于文献[10]中遗传算法编码方式的思想对标准遗传算法进行改进，通过Cramer-Rao不等式求解编队构型评价的适应度函数，完成多节点分组协同定位的编队构型实时动态优化；最后通过仿真验证了所提出方法的有效性和稳定性。

1 并行式多节点协同系统的编队构型评估

多节点协同定位系统中，每个节点利用自身传感器进行融合定位的同时，还可以通过UWB 传感器测量节点之间的相对距离，实现协同导航信息的融合和单体定位精度的优化。并行式多节点协同定位的方案如图1 所示，本文以节点间测距信息作为容积卡尔曼滤波的量测信息，为每个节点建立局部滤波器，实现系统中各个节点的位置更新。

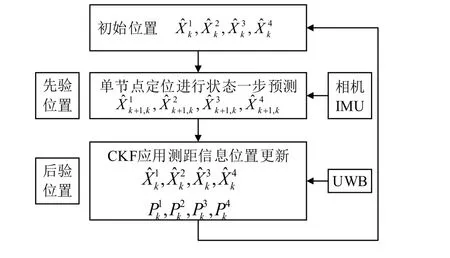
图1 CKF 协同算法Fig.1 Cubature Kalman filtering collaborative algorithm

并行式多节点系统进行协同定位时，节点编队构型对协同定位精度起着至关重要的作用。多节点协同定位是一个状态预测过程，因此可以使用预测误差协方差来评价协同定位性能的优劣。Cramer-Rao 不等式从理论上给出了位置参数无偏估计的协方差矩阵的下界，它的倒数为Fisher 信息量，其常被用来描述预测过程中量测值所包含的状态变量信息量的大小。Fisher信息量越大，模型本身所能提供的信息量就越多，相应地，不确定性就越小，预测性能也就越良好。

应用Cramer-Rao 边界不等式，对并行式多节点协同定位算法所达到的定位误差方差下界进行分析。对于由N个节点构成的协同定位系统，节点n与其可通信节点实现协同定位，则节点n的Fisher 信息矩阵为：

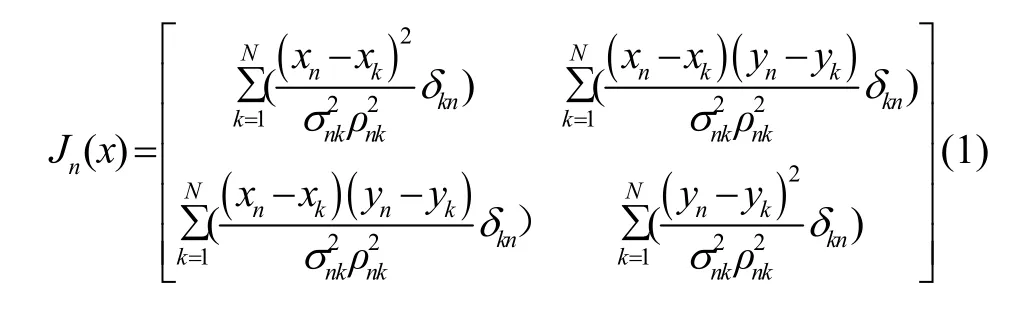
其中，xn、yn表示节点n位置信息；ρnk为节点n与节点k间测距距离；σnk为节点n与节点k间测距误差；δkn为狄利克雷函数，当节点n与节点k间进行协同，δkn取值为1，反之则为0。

2 基于改进遗传算法的编队优化算法

遗传算法是一种模仿自然法则的启发式随机搜索算法，可通过模拟选择、交叉、变异等关键操作达到全局搜索的目的，进而求得问题最优解。当协同导航系统中节点数目过多时，受通信带宽以及传感器测距范围等限制，实际系统中的每个节点很难同其它所有节点的通信和测距。本文提出一种改进的遗传算法，将多节点协同系统分为多个子编队进行协同定位，实现了系统中节点间局部的通信和协同，并通过对遗传算法的改进提高计算效率。对于遗传算法的改进具体如下：

（1）染色体编码：考虑子编队中节点数目范围、节点间测距限制等约束条件；

（2）染色体交叉：以“染色体列”形式交叉，从而保证每个节点始终至少包含在一个子编队中；

（3）染色体变异：在完成标准染色体变异过程后，对变异后的染色体进行约束条件检验，若符合检验则进行变异；优先通过染色体变异将静止节点添加到染色体编码表示的编队中。

2.1 种群初始化

种群中每个染色体代表多节点协同系统的一种编队构型。本文对标准遗传算法的染色体初始化方式进行改进使其满足协同定位的约束条件，约束条件如下：

（1）每个子编队中的节点数目ni应该满足设定的限制条件，即ni∈[nmin,nmax]；

（2）每个节点至少参与一个子编队的协同定位；

（3）种群染色体所代表的编队构型应满足实际测距信息的限制条件，如：若节点2 与节点5 间测距信息无法获得，则任意子编队中不同时包含这两个节点。

图2 为一个初始化后的染色体编码，由M行N列的“01”编码组成，其中M为系统子编队个数，N为系统节点总数，ni为每个子编队包含的节点数目。为满足约束条件，染色体编码每行含有ni个“1”编码，每列至少含有1 个“1”编码，且满足测距限制。如图2 所示第一行编码代表第一个子编队是节点2、节点5、节点9 和节点10 构成的四节点编队。

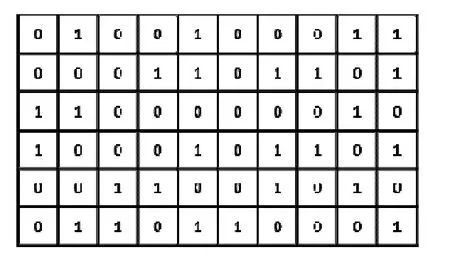
图2 染色体编码方式Fig.2 Mode of chromosomal code

对于含有N个节点的协同系统，协同定位精度随着子编队数目M和编队包含的节点数目ni增加而提高，但算法的计算量与通信量均与M和ni正相关，故子编队数目M和编队节点数目ni的上限受系统通信带宽和计算单元算力限制。由容积卡尔曼滤波算法的可观测性分析，子编队节点数目ni至少为3。

初始化具体方法为：初始化时按行初始化，首先生成随机数n1(n1∈[3,5])，并产生n1个“1”编码随机分配到染色体编码的第一行，且随机分配过程需满足测距信息限制，最后将其余位置设为“0”编码，以此方法完成1～M-1行编码。初始化第M行时，首先检查染色体编码中不包含“1”编码的列，令该列最后一行首先为“1”编码，如图2 中令(6,6)位置为“1”编码。若剩余“1”编码，将剩余“1”编码随机分配，至此完成满足约束条件的种群初始化。

2.2 适应度函数和种群优选

种群中染色体适应度值的计算由Cramer-Rao 不等式进行求解，遗传算法中整个种群的最佳适应度为：

其中，s为染色体编号，h为遗传代数，ghs为第h代第s条染色体适应度：

其中，J表示N个节点构成的协同定位系统的Fisher信息矩阵，Jn表示节点n的Fisher 信息矩阵。

染色体选择采用轮盘赌法对种群中染色体进行优选，产生的下代种群数目与初始种群数目相等。算法优化的目标函数为协同系统的平方位置误差界，当染色体的适应度函数值越小时，其在遗传过程中被选中的概率越大，染色体基因对应编队构型遗传到下一代的概率越大。

2.3 染色体交叉

图3 为染色体交叉方式。首先，将优选后的种群中染色体随机两两配对，作为父染色体和母染色体，按照交叉概率决定是否对其进行交叉运算。为了减少由于交叉运算后个体染色体不满足约束条件将其丢弃会造成的无效计算量，改进算法在父母染色体中随机选择相同位置的“染色体列”为交叉区域进行交叉操作，避免交叉后染色体不满足2.1 节中约束条件（2）。在交叉运算后需要对子染色体进行约束条件（1）和约束条件（3）检验，符合条件则用两个子染色体代替父母染色体，反之则取消该对父母染色体的交叉操作，保留原父母染色体作为种群个体。

图3 染色体交叉方式Fig.3 Mode of chromosomal crossover

2.4 染色体变异

变异操作是为了防止算法陷入局部最优，由于每个染色体结构由M个子编队组成，所以在进行变异操作时对于每个子编队分别按照变异概率随机产生编码突变位置，然后在变异过程中进行约束条件检验。在图4 中，染色体中子编队2 和子编队4 产生突变位置分别为(2,4)、(4,6)，其余编队未产生突变位置。假设节点间均可测距，(2,4)编码通过约束条件检验可以进行突变，(4,6)编码突变后导致n4=6＞nmax，所以未进行突变。与染色体交叉操作相似，在染色体变异过程中加入对约束条件的检测，可以最大程度地避免种群在寻求最优解过程中的无效变异，从而减小计算量、提高计算效率。

图4 染色体变异方式Fig.4 Mode of chromosomal variation

由单体节点自身定位算法特性，在静止状态下节点定位误差随时间漂移较小。在染色体变异过程中考虑单体运动学约束，当子编队中代表静止节点的编码为“0”编码，则将其首先变异为“1”编码。

2.5 算法整体流程

基于改进遗传算法的多节点系统动态分组的协同定位算法流程如图5 所示。算法伪代码如表1 所示。

图5 算法整体框架Fig.5 Overall framework of the algorithm

表1 整体算法伪代码Tab.1 Overall algorithm pseudo code

3 仿真试验

3.1 仿真环境

试验仿真平台为Intel(R) Core(TM) i9-10940X CPU，32GB 内存，基于x64 的处理器的台式机，编程语言为C++，仿真软件为Linux 操作系统下Gazebo物理仿真模拟器。单体节点通过基于单目视觉与IMU融合的无回环SLAM 方案实现自身定位，单体无人车仿真框架如图6 所示。

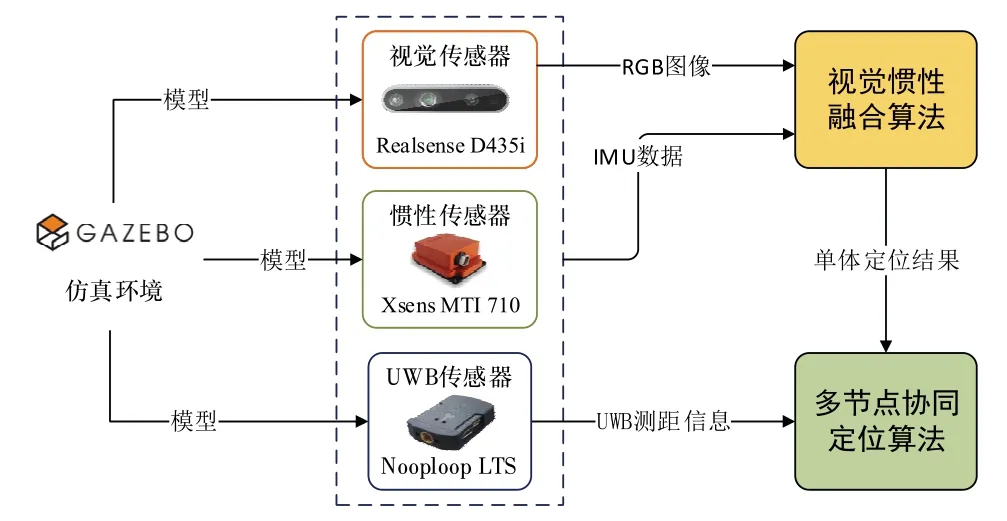
图6 无人车仿真框架Fig.6 Unmanned vehicle simulation framework

试验中传感器数据均来自Gazebo 环境下搭建的传感器模型，建模选用的传感器型号如图6 所示，其中英特尔Realsense D435i 深度相机的RGB 图像分辨率为640×480，Xsens 公司的MTI 710 型号惯性传感器的加速度计零偏稳定性为40μg，陀螺仪零偏稳定性为10°/h。节点间测距采用Nooploop LTS 型号的UWB传感器，其测距精度为0.4m。

3.2 仿真试验1

协同定位系统由10 个自由运动的节点组成，节点最大运动速度为1m/s，每个协同子编队的节点数目为3～5 个，容积卡尔曼滤波协同频率为1Hz，仿真总时长为2h，仿真中各节点实际运行轨迹如图7 所示，节点按图中轨迹进行往复运动，各节点运动总路程约为3.5km。

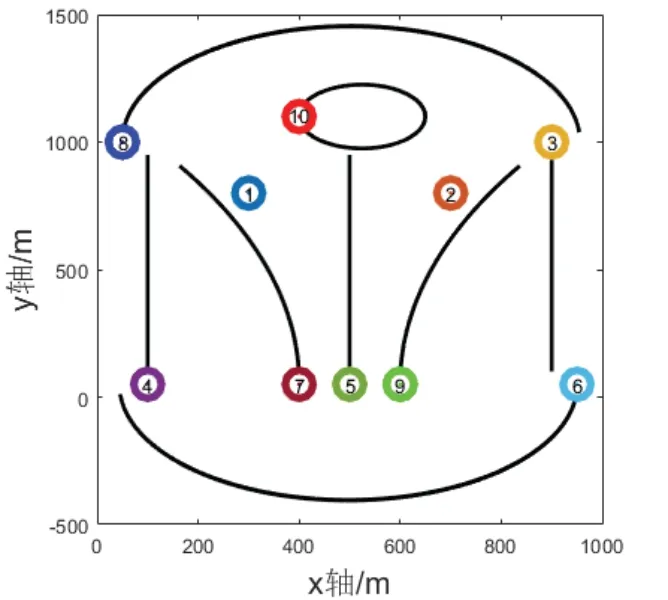
图7 节点运动轨迹Fig.7 Node movement trajectory

基于上述仿真条件，对10 个节点进行仿真试验，给出单体自身视觉惯性里程计定位、在固定编队下协同定位、在动态编队下协同定位的距离均方根差（DRMS）对比。表2 列出系统中10 个节点三种定位方法的均方误差最大值，选取进行直线运动的节点5和回旋运动的节点7 绘制其均方根差对比曲线，如图8-9 所示。图10 为节点7 在运动过程中进行协同定位的子编队构型变化。

对试验结果分析如下：

（1）由图8 和图9 可以看出，基于UWB 测距信息的CKF 协同定位算法可以显著抑制单节点定位精度随时间的漂移，从而提高单节点定位的精度；

图8 节点5 误差对比曲线Fig.8 Node 5 error comparison curve

图9 节点7 误差对比曲线Fig.9 Node 7 error comparison curve

（2）由图10 可以看出，随节点间相对位置发生变化，当系统编队不能满足编队构型的评价指标要求，会触发改进遗传算法对编队构型进行实时更新；

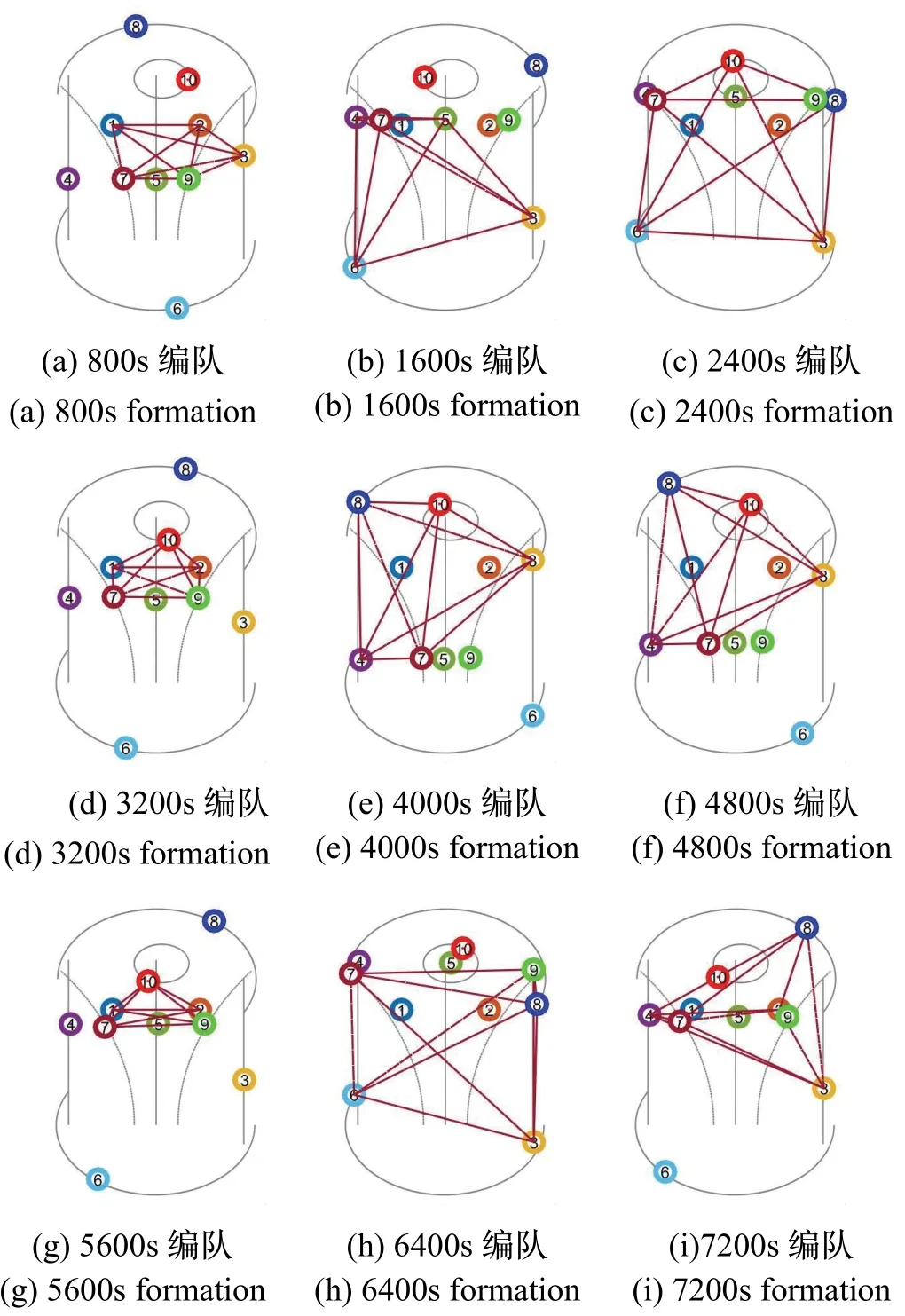
图10 节点7 子编队构型变化Fig.10 Node 7 sub-formation configuration change

（3）由表2 可以看出，动态编队协同定位各节点的定位均方误差与固定编队构型相比均有所下降，平均下降了36%，其中最优下降了69%，最劣下降了13%，验证了改进的遗传算法可以有效地完成多节点系统协同导航的编队优化。

表2 节点定位的均方误差最大值Tab.2 The maximum mean squared error for node positioning

3.3 仿真试验2

为验证节点数目对改进遗传算法收敛性和在线编队优化有效性的影响，分别对10 个节点、20 个节点和50 个节点构成的协同系统进行仿真试验。编队优化算法考虑实际系统中多种约束限制，对遗传算法的初始化编码、染色体交叉、染色体变异等进行了改进，试验中遗传算法种群大小为100，最大迭代次数为200，交叉概率和变异概率分别为0.5 和0.6。表3 列出了三种节点系统中编队优化的约束参数。

表3 编队约束参数Tab.3 Formation constraint parameters

表4 给出了标准遗传算法和改进遗传算法对三种节点系统完成一次编队优化的时间对比，表中数据为算法运行50 次的平均值。

表4 遗传算法运行时间对比Tab.4 Genetic algorithm running time comparison

表5 给出了三种节点系统在固定编队下和应用改进遗传算法优化的动态编队下协同定位的误差对比。如表5 所示，10、20、50 节点系统的动态编队节点协同定位的精度相较于固定编队均有提升，且改进的遗传算法收敛速度也较快，验证了该算法具有有效性和可行性。

4 结论

为解决协同导航中协同节点的选取问题，本文提出了一种基于改进遗传算法的动态分组编队构型优化算法，主要得出以下结论：

（1）基于改进遗传算法的多节点动态编队的协同定位算法能够有效地提升协同导航系统中各节点的定位精度。针对10、20、50 节点系统，动态编队下节点的协同定位精度较固定编队均有提升：10 节点协同系统的定位误差平均降低了36%，其中最优降低了69%，最劣降低了13%；

（2）改进的遗传算法在编码、交叉和变异操作中构建动态编队分组的约束条件，有效降低了遗传算法的无效计算量。对于50 节点系统，算法平均求解时间为0.394 s，仿真试验验证了本文所提算法的有效性和可行性。