六西格玛约束磁力计在线校准方法

刘 宇，韩 亮，冯 涛，杨 杰，陈燕苹

（重庆邮电大学 光电工程学院，重庆 400065）

惯性导航航向偏移的根本原因是陀螺仪偏移[1]，磁力计可计算绝对航向，且无累积误差，已成为修正惯性导航航向的重要传感器之一[2-4]。受环境影响，磁力计在测量地球磁场时会存在磁干扰误差，因此研究如何在动态磁干扰环境下测量获取精确的地球磁场是抑制惯性导航航向偏移的关键。

目前，磁力计校准方法分为离线校准和在线校准：前者的磁力计校准模型精度高，初始校准后不再更新，精度受动态磁干扰的影响大；后者的磁力计校准模型随磁干扰的变化进行在线更新，可抑制动态磁干扰对其精度影响，但其精度较前者低。

王海涌等人利用加速度和地磁场点积不变的原理补偿陀螺仪偏移[5]，若地磁信息通过离线校准模型获得，则在补偿陀螺仪偏移时会引入动态磁干扰，导致航向精度发散。李磊磊等人利用磁航向约束视觉惯性定位[6]，若存在动态磁干扰，磁航向会存在误差，影响定位精度。为校准动态磁干扰，Wu 等人利用姿态角对动态磁干扰进行实时估计并校准[7]，但陀螺仪偏移会错误估计动态磁干扰，导致模型精度下降。Cao等人利用最大似然估计法（Maximum Likelihood,ML）和最小二乘法（Recursive Least Square,RLS）对模型进行递推更新[8]，但陀螺仪参与校准，模型精度会受陀螺仪漂移影响。为解决上述问题，原雨佳等人利用双目标函数粒子群优化对磁干扰进行校准[9]，虽然陀螺仪和磁力计构建的双目标函数可以抑制陀螺仪漂移带来的误差，但该误差会随时间增加。Liu 等人将绝对姿态转换矩阵推导的磁力计理论输出和实际输出之间的误差，利用迭代的方法，展开成了多组相对姿态转换矩阵更新下一时刻磁力计理论输出和实际输出之间的误差，误差中由相邻时刻陀螺仪漂移产生的误差可忽略不计，所以求解使展开的多组误差最小的校准系数，可消除因陀螺仪漂移引入校准系数的误差[10]，但该方法需要从初始姿态迭代，包含了陀螺仪和磁力计所有历史值的计算，运算量大，校准模型的实时性差，精度低。上述在线校准方法都存在依靠惯性传感器辅助导致模型精度随时间增加而下降的问题。此外，构建的磁力计误差模型精度会影响到磁干扰的校准效果，王木华等人利用RLS 更新校准模型[11]，但简化的磁力计误差模型不适用于复杂的地面磁场环境。Iqbal等人构建了较为精确的磁力计误差模型并求解了模型系数[12]，但模型中并没有考虑到高斯白噪声误差对模型的影响，不适用于在线校准方法。

基于以上分析，本文提出了一种无惯性传感器辅助更高精度和稳定性的磁力计在线校准方法。本文首先分析了磁力计误差并建立了精确的磁力计误差模型；其次使用六西格玛（Six Sigma,SS）实现对磁力计校准模型的管理和磁力计误差的分类；然后推导了六西格玛约束扩展卡尔曼滤波方程；最后基于CHY_IMU11 样机开展了实验和数据处理，并与传统方法做对比，验证所提出算法的有效性。

1 磁力计输入输出模型

磁力计器件误差主要包括刻度因子误差、零偏误差、非正交误差、安装误差和高斯白噪声误差，由此得磁力计输入输出模型如下：

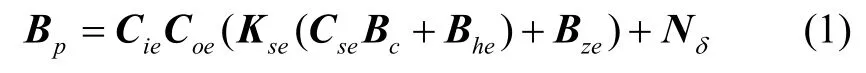
其中，Kse是3×3 的刻度因子误差矩阵；Bze是3×1的零偏误差向量；Bhe是3×1 的硬磁干扰向量；Bc是3×1 的理论测量向量；C se是软磁干扰矩阵；C oe是3×3的非正交误差矩阵；C ie是3×3 的安装误差矩阵；Nδ是3×1 的高斯白噪声误差向量；Bp是3×1 的磁力计实际测量向量。

将式(1)展开如下：

令：

简化可得：

其中，W是3×3 的综合软磁干扰误差矩阵，是软磁干扰误差和器件误差耦合的结果，随环境变化，为方便求解，W被定义为正定实对称矩阵；V是3×1 的综合硬磁干扰误差向量，是硬磁干扰误差和器件误差耦合的结果，不随环境变化。

2 六西格玛磁力计校准模型优化管理

六西格玛是一种管理策略，是由1986 年摩托罗拉任职的工程师比尔·史密斯提出的。六西格玛主要是通过设定的目标来采集相关数据，分析得出的结果与设定的目标比较，找出产品存在的缺陷加以改进，进而减少次品率，提高服务质量[13]。而磁力计校准模型可以利用六西格玛进行优化管理，通过计算模型输出结果和目标结果之间的误差大小找出模型的缺陷所在，即判断磁力计误差的种类，并加以校准。

首先，设定六西格玛优化管理磁力计校准模型的目标。离线校准方法得到的高精度磁力计校准模型可作为设置管理目标的参考。在稳定磁场中采集磁力计的n个数据用于椭球拟合（Ellipsoidal Fitting,EF）求解初始磁力计校准模型，结果如式(5)所示：

其中，W0是3×3 的初始综合软磁干扰误差矩阵；V0是3×1 的初始综合硬磁干扰误差向量。

在磁场稳定的环境下，W稳定不变，V因为存在高斯白噪声项，所以值会在V0附近随机变化，此时磁力计的n个输出结果Bci（i=1,2,3,…,n）的磁场强度服从分布：

综上所述，将六西格玛优化管理磁力计校准模型的目标设定为：在磁场稳定时，磁力计输出的磁场强度范围为[μ0-6σ0,μ0+6σ0]。

判断磁场是否稳定可通过六西格玛实现。六西格玛可根据系统结果的离散程度将系统的质量等级分为六个级别，表示若有100 万次出错机会，分别可能出现错误的次数[13]。系统质量等级和出错概率对应关系如表1 所示。

表1 系统质量等级和出错概率对应关系表Tab.1 Correspondence between system quality level and error probability

磁力计校准模型为待测系统，磁力计输出为系统结果，磁力计输出的磁场强度在目标之外的概率为出错概率。出错概率越低，磁力计校准模型的质量等级越高，磁干扰就越小。综上所述，可得系统质量等级和磁干扰等级的对应关系。如表2 所示。

表2 系统质量等级和磁干扰等级对应关系表Tab.2 Correspondence between system quality level and magnetic interference level

本文使用一个长度为L的滑动窗口来采集磁力计数据计算实时的磁干扰等级，其步骤如下：

利用k时刻磁力计校准模型计算滑动窗口中磁力计输出的磁场强度均值μk、方差和出错概率pk：

k时刻磁力计校准模型的质量等级Mk由式(11)确定。当Mk=6时，磁干扰等级为0，磁场稳定，磁力计输出结果的误差由高斯白噪声引起；当Mk＜ 6时，磁干扰等级不为0，磁场不稳定，存在动态磁干扰，需在线校准，更新综合软磁干扰误差矩阵Wk。

通过六西格玛实现磁干扰误差和高斯白噪声误差的精确分类，避免将高斯白噪声错误当成磁干扰进行校准时给磁力计校准模型引入误差的问题，使求解的Wk更接近真实值，进而提升模型精度。

3 六西格玛约束扩展卡尔曼滤波

3.1 六西格玛约束扩展卡尔曼滤波的时间更新

根据磁力计误差模型的分析，SEKF 的状态向量表示如下：

其中，ωij（i,j=1,2,3）是W-1中第i行，第j列的元素，是综合软磁干扰校准矩阵系数。

SEKF 时间更新如下：

其中，F k是6×6 的状态更新矩阵，磁场稳定时为单位矩阵 I6×6；Q w是过程噪声协方差矩阵；P k是估计的状态协方差矩阵。

3.2 六西格玛约束扩展卡尔曼滤波的测量更新

当Mk＜ 6时，磁场不稳定，通过SEKF 测量更新实现磁干扰误差校准。其本质是根据六西格玛优化管理目标对EKF 的测量更新进行改进，使得状态估计与真实状态wk之间误差最小的同时，还能满足六西格玛约束条件Mk=6。所以SEKF 可等效为求解带约束条件的目标函数，如式(14)所示：

根据式(15)，六西格玛约束条件等效如下：

根据六西格玛原理，式(16)进一步等效如下：

所以，式(14)可等效如下：

拉格朗日乘子法可将约束条件和目标函数的最优化问题转换成函数极值的求解问题：

SEKF 测量更新如下：

3.3 高斯白噪声校准

当Mk=6时，磁场稳定，磁力计误差由高斯白噪声引起。使用SEKF 校准高斯白噪声误差，状态向量如下所示：

时间更新：

测量更新：

其中，P0是3×3 的状态协方差矩阵，为单位矩阵 I3×3；A是3×3 的状态转移矩阵，无高斯白噪声时为 I3×3。

4 实验验证

4.1 实验条件

为验证SEKF 方法校准磁力计的效果，本文在具有典型动态磁干扰的环境下进行实验验证。实验测试轨迹为长约50 米，宽约10 米，串联室内外磁场环境的矩形。室内走廊约40 米，两侧存在各种金属物品，磁场环境多变。室外磁场相对室内稳定，但存在井盖和车辆等金属物品改变磁场环境。轨迹将室内外磁场环境串联，构成一个存在动态磁干扰的实验场景。矩形轨迹的卫星图如图1 所示，蓝点为起点或终点，测试者按照黄色箭头方向进行测试。

图1 实验轨迹卫星图Fig.1 Satellite map of experimental trajectory

采集数据的仪器为CHY_IMU11，拥有三轴陀螺仪、三轴加速度计和三轴磁力计，采样频率为100 Hz。实验测试时将仪器固定于测试人员脚后跟处，并沿实验测试轨迹，进行矩形绕圈测试，采集数据时间约30 min，测试人员回到起点结束采样。

4.2 实验数据处理

SEKF 的滑动窗口长度L设为200，当Mk＜ 6时SEKF 校准磁干扰误差，当Mk=6时SEKF 校准高斯白噪声误差。整体流程如图2 所示。

图2 SEKF 流程图Fig.2 SEKF Process

实验中的参考航向依据出发前静止时刻姿态仪与地磁北向的夹角和矩形轨迹计算得到。为验证本文方法有效性，实验增加了对比组，包括陀螺仪辅助（Gyroscope assistance,GA）方法和扩展卡尔曼滤波（Extended Kalman Filter,EKF）方法。实验结果如图3所示。

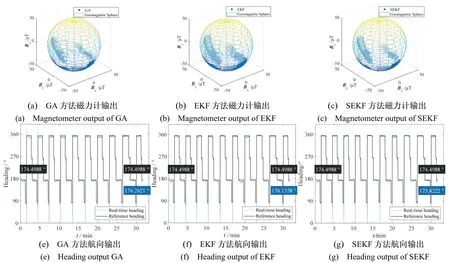
图3 实验结果Fig.3 Experimental results

4.3 实验数据分析

GA 方法是利用惯性测量单元更新的四元数计算的磁力计理论输出辅助磁力计校准的方法，是一种相对校准方法。当初始校准模型与启动环境的磁场匹配度低时，初始航向与绝对航向存在误差，且无法在后续过程中校准。如图3(e)所示，前期与参考航向稳定存在一个较小的相对误差，直到陀螺仪出现漂移。航向偏移与陀螺仪精度相关，陀螺仪精度越高，航向偏移越慢、最终偏移值越小；陀螺仪精度越低，航向偏移越快、最终偏移值越大。该效果在下文图5 中更为明显。

EKF方法是只通过磁力计自身测量值进行校准的方法。由于没有磁力计误差分类，所以高斯白噪声被当作磁干扰进行校准，给模型引入了误差。如图3(f)所示，虽然整体航向更贴近参考航向，但局部误差更大，特别是180 °附近，实时航向多次偏离参考航向，最大偏差达到10.5458 °。

SEKF 方法是六西格玛管理下的、无惯性传感器辅助的校准方法，是一种绝对校准方法。如图3(g)所示，即使初始航向与绝对航向存在误差，也会被快速校准。磁力计误差中高斯白噪声误差和磁干扰误差被分类校准，获得了更高精度的磁力计校准模型。与对比组方法相比，SEKF 方法的实时航向在整体和局部上与参考航向的贴合度最高。

本文将磁力计校准模型输出结果的磁场强度RMSE（RMSEM）、误差比（EPM）、航向RMSE（RMSEH）、闭环误差（Closed Loop Error,CLS）和平均单次运行时间（Average Single Run Time,ASRT）作为性能参数来量化各类方法对磁干扰的校准效果和实时性。表达式如下：

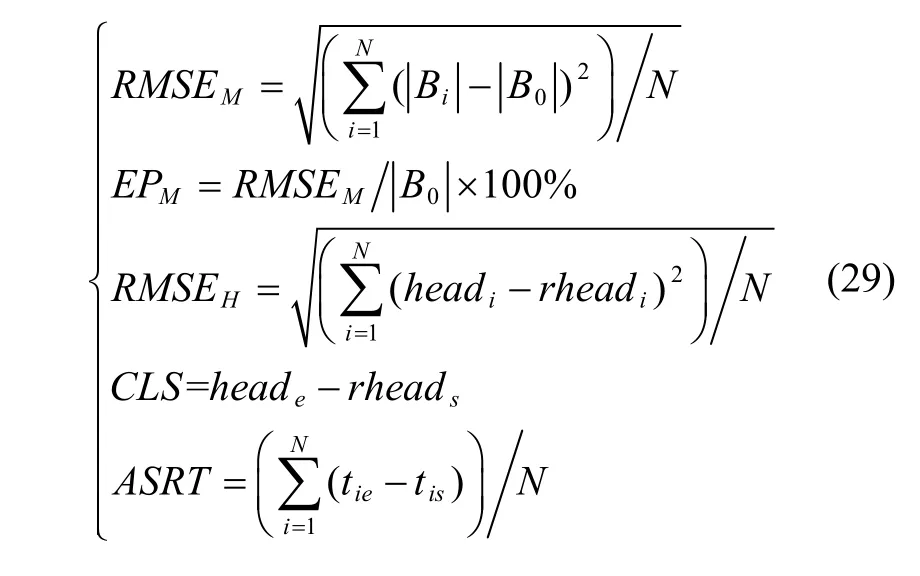
其中，N是采集到的数据帧总数；rheadi是i时刻的参考航向；headi是i时刻的实时航向；rheads是出发前的参考航向；heade是结束时的实时航向；tis是程序执行到第i次运算时采集到数据的时刻；tie是程序执行到第i次运算时航向求解结束的时刻。

上述所有方法的具体性能参数如表3 所示。

表3 各类磁力计校准方法的性能参数表Tab.3 Performance parameters for each type of magnetometer calibration method

从表3 中可知各方法对磁力计校准精度的差异主要体现在航向修正结果的RMSEH和CLS上。相较于CLS，RMSEH能更好地体现过程中各方法对动态磁干扰的在线校准效果，且实验过程必然无法保证结束时的绝对航向与出发前一致。因此，本文选择RMSEH作为关键性能参数来评价各方法对磁力计在线校准的效果。表3 中，SEKF 方法的RMSEH最小，为3.0739 °，对磁力计校准的效果最好。

由实验条件可知，传感器采集数据、磁力计在线校准、航向角修正所消耗的总时长应小于等于10 ms。从表3 中可知GA、EKF、SEKF 的ASRT均在1 ms以下，满足磁力计在线校准的实时性要求。GA 方法因为有惯性姿态角辅助磁力计校准，测量矩阵计算相对简单，所以整体运算速度更快。EKF 方法没有外部惯性传感器辅助，测量矩阵计算相对更复杂，所以整体运算速度稍慢。SEKF 要先计算滑动窗口中的出错概率pk，判断误差，分类校准，运算量相对较大，所以整体运算速度最慢。整体而言，SEKF 在实现了更准确的磁力计误差类别判断，更高精度的磁力计校准模型求解和更稳定的航向保持的同时，运行时间也能满足实时性要求。

为进一步验证本方法的优势，本文在数据处理过程中，向陀螺仪数据引入了5 个不同的额外零偏不稳定性（Additional Bias Instability,ABI）来模拟5 种不同精度的陀螺仪，并计算各方法的RMSEH，结果如图4 所示。从图4 中可知：GA 方法的RMSEH随着ABI 变大而变大。其原因为：当陀螺仪精度越低时，陀螺仪的零偏稳定性越差，偏移速度越快，对磁力计输出在磁场方向上引入的误差越大，航向修正效果越差，如图5 所示。

图4 不同ABI 下各方法的RMSEHFig.4 RMSEHof each method under different ABI

图5 ABI 为2 °/h 时GA 方法的航向输出Fig.5 Heading output of GA at ABI of 2 °/h

此外，图4 中SEKF 方法和EKF 方法相较于GA方法，RMSEH都更加稳定，且SEKF 方法的RMSEH一直保持最小。SEKF 方法相较于对比组方法的磁力计校准效果的相对提升百分比，可用RMSEH减少的相对百分比来表示。整理其结果如表4 所示。

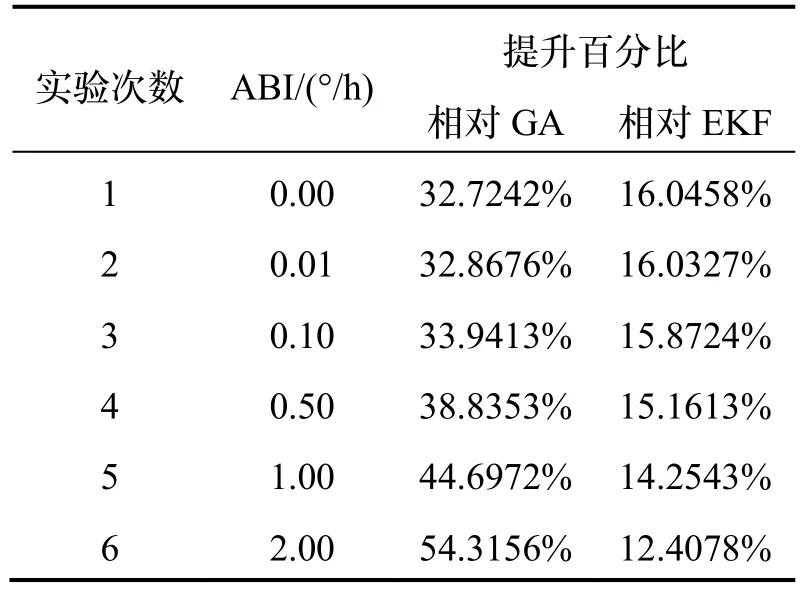
表4 SEKF 方法磁力计校准效果相对其他算法提升百分比Tab.4 Relative percentage improvement of the magnetometer calibration effect of the SEKF method

5 结论

本文提出一种基于磁力计误差分类的、无惯性传感器辅助的在线校准方法，解决了传统磁力计在线校准方法需要惯性传感器辅助，精度不稳定，计算复杂的问题。首先，分析了磁力计误差，并构建了精确的磁力计误差模型。其次，使用六西格玛对磁力计校准模型进行管理，实现了磁力计误差分类。最后，使用SEKF 方法完成磁力计误差的校准。实验结果表明，SEKF 方法的航向RMSE 相对于GA 方法降低了32%以上，相对于EKF 方法降低了12%以上，说明SEKF方法的磁力计校准效果相比于对照组方法更好，且在不同精度陀螺仪的测试下，也能够长时间保持高精度和高稳定性。在未来的工作中，针对固定滑动窗口长度L无法应对磁场变化速度较快环境的问题，可以考虑根据磁场变化速度动态调节滑动窗口长度L，增加磁力计数据的利用率，进一步提升算法的精度和适用性。