基于置信规则库的冗余惯导在线故障诊断与重构方法

张东波，汪立新

（火箭军工程大学，西安 710025）

随着我国航空航天、武器装备等领域的发展，火箭、导弹等飞行器装备数量、使用频次急剧增加。因此，如何在降低其生产、维护成本的同时提高其健康管理水平是需要重点解决的问题之一[1-3]。

惯导系统作为火箭、导弹等飞行器控制系统的关键部件，其旨在对飞行器的位置、姿态等信息进行采集，是飞行器实现时序飞行、变轨突防的关键。多表冗余惯导系统通过用多个成本较低的陀螺仪、加速度计的交叉耦合，以提高惯导系统的精度和可靠度，同时降低了惯导系统的设计成本。

多表冗余惯导系统故障诊断与重构旨在根据多个陀螺仪、加速度计的测试信息对其开展在线故障检测、诊断、定位，并根据故障诊断结果，利用剩余可用同类相关陀螺仪、加速度计开展故障陀螺仪、加速度计信息重构，以保证惯导系统输出信息的准确性[4-8]。

目前多表冗余惯导系统故障诊断与重构主要面临三个方面的问题：首先，飞行器惯导系统中所使用的陀螺仪、加速度计等传感器均属于军品级，筛选过程严格，设计可靠性较高，进而导致其在使用过程中出现故障的概率较低，长周期通电状态下所获取的数据多数为惯导系统正常状态下的数据，故障状态下的数据较少[9]。其次，多表冗余设计下的惯导系统由多个陀螺仪、加速度计组成，受其飞行环境不确定性、不可预测性和多飞行状态切换、部件安装误差等因素的影响，输出结果具有一定的不确定性和随机性[10]。最后，飞行器在飞行过程中速度较快，惯导系统一旦出现故障需要在最短时间内检测、诊断、定位故障，进而快速进行重构容错，降低惯导系统故障给飞行器控制系统所带来的影响，确保飞行器飞行过程的稳定性。因此，在线故障诊断与容错重构的实时性是需要重点关注的性能之一。

置信规则库（Belief rule base,BRB）作为专家系统的一种，是基于证据推理、IF-THEN 规则、模糊理论等理论发展而来的。BRB 模型通过专家初始建立、数据学习训练的方式将知识与数据有效融合，同时通过证据推理融合克服知识不确定性所带来的影响[11-15]。由于BRB 在小样本建模中所具有的优良性能，其被广泛应用于故障诊断、安全性评估、医学决策等领域。

针对多表冗余设计方案下惯导系统故障诊断与重构过程中所面临的三个难题：故障状态下数据缺乏、专家知识不确定性和高实时性要求，本文基于BRB构建了一种故障诊断与重构框架，通过融合专家知识和测试数据最大化利用系统信息，并采用了故障传感器输出重构策略对惯导系统内部传感器故障进行容错；为了进一步提高模型实时性，设计了一种新的基于输出误差影响度自适应扩散的在线更新信息调整策略，通过BRB 模型输出误差对故障诊断和重构模型在线更新的信息量进行反馈调节，在使其精度满足应用要求的同时提高在线建模的实时性，有效处理精度与实时性之间的冲突；为克服专家不确定性对模型精度的影响，构建了考虑模型参数物理意义的优化模型，通过少量不平衡数据对模型进行学习，进而达到数据与知识的混合。

1 基于BRB 的多表冗余惯导系统故障诊断与重构

本节对基于BRB 的惯导系统故障诊断与重构模型过程进行了推理，如图1 所示。首先由专家结合其自身经验给定模型的初始参数，在惯导系统的监测信息可用后，对惯导系统开展故障诊断，并根据故障诊断结果对其内部故障的加速度计/陀螺仪开展重构，进而保证惯导系统输出信息的可靠性。

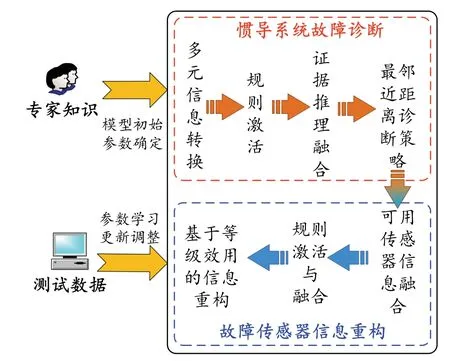
图1 惯导系统故障诊断与重构框架Fig.1 Fault diagnosis and reconstruction framework of inertial navigation system

1.1 惯导系统故障诊断模型推理

在基于BRB 的惯导系统故障诊断模型中，其输入信息为惯导系统的测试信息、输出为惯导系统中陀螺仪和加速度计等传感器的故障情况。惯导系统故障诊断模型推理过程主要分为四步，即信息转换、规则激活、证据推理（Evidential reasoning,ER）规则融合与输出诊断。

Step 1：多元监测信息转换

由于惯导系统中的陀螺仪、加速度计等传感器的监测信息格式、量级各不相同，无法直接融合使用，需要将多元监测信息转换到统一框架下：

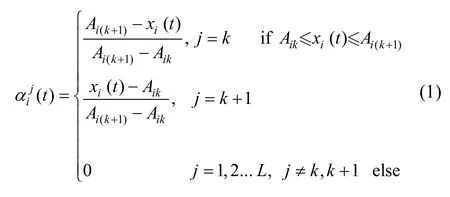
式中，x1(t),x2(t) …xM(t)表示惯导系统的M个监测指标的监测信息，为故障诊断模型中第i个监测指标的输入信息相对于第j条规则匹配度[7-10]。Aik和Ai(k+1)分别为两条相邻规则的参考等级，主要按照如下三个原则进行确定：涵盖数据变化范围、间距合理、数量适中。L为模型中规则数量。首先，参考等级需要涵盖监测指标的波动范围，以防止超出波动范围后数据无法转换；其次，参考等级之间的距离决定了信息转换的精度，距离太近会导致所需的参考等级数量过多，距离太远会导致转换精度降低；最后，参考等级的数量直接决定了规则库中的规则数量，尤其在监测指标多时，每个指标的参考等级数量会影响模型的可实施性。

Step 2：规则激活

在BRB 模型中，不同规则中所包含的监测指标参考等级不同，在监测信息输入到故障诊断模型中时对于规则的激活程度也不同。结合上述信息转换过程中所获取的监测信息匹配度，可以得到规则中所有监测指标信息相对于该条规则匹配度：

式中，αk(t)为t时刻模型指标输入信息相对于第k条规则的总体匹配度；分别为第i条监测指标的权重和相对权重；M为指标的个数。

在得到指标输入信息相对于每条规则的匹配度后，可以进一步计算得到该条规则的激活程度，即激活权重。

式中，wk(t)为第k条规则的激活权重；θk(t)表示第k条规则在规则库中的权重，L为模型中规则的数量。

Step 3：ER 算法规则融合

在故障诊断模型中，不同的规则的激活权重不同，在整个规则库中所发挥的作用也不同，并且每条规则输出结果中的匹配度也不同。因此，需要通过ER 算法对模型中的规则进行融合，以得到最终各个故障状态的置信度。

ER 算法如下式所示：

式中，βn(t)为融合L条规则后第n个系统故障状态的置信度；βj,k(t)表示规则输出的置信度；μ、Δn(t)和μ(t)分别为ER 算法的中间系数，无物理意义；N表示输出结果中的故障状态或参考等级的个数。

Step 4：最邻近距离故障诊断策略

ER 融合后的输出结果为惯导系统各故障状态的置信度，即β(t)=[β1(t),β2(t)…βN(t)]。为了进一步确定当前时刻惯导系统的故障状态，本文采用了基于最邻近距离的故障诊断策略：

式中，Ε为惯导系统标准故障向量，Eni为标准故障向量的参考值；J为范数的阶次，其具体数值由专家给定。

根据故障诊断模型输出向量与标准故障向量之间的距离，当前时刻惯导系统的故障状态为：

其中，En和Ee分别为第n个和第e个标准故障向量。

基于上述最临近距离的计算公式，可以判断当前时刻惯导系统的故障状态为第e种。本文针对的惯导系统故障为加速度计和陀螺仪等传感器由于长时间通电所导致的恒偏差、漂移、性能退化等非致命性故障，并假设惯导系统同一时刻仅有一个传感器发生故障，即故障状态为加速度计故障或陀螺仪故障。

1.2 故障传感器输出重构模型推理

在故障传感器输出重构模型中，其推理过程与上节故障诊断模型相似，区别在于故障传感器输出重构模型中的输入指标为其相同类型可用传感器的监测信息，其对应的指标参考等级根据输入指标确定。输出重构模型规则输出中的{H1,H2…HN}需要根据故障传感器监测信息确定。

在经过ER 算法融合后，模型输出的结果为各参考等级的置信度β(t)。故障传感器输出重构属于典型的拟合类输出，需要进一步将置信度向量转换为重构输出：

式中，c f(t)为t时刻重构后故障传感器的监测信息。u(b)为输出重构模型中第b个参考等级效用值，B为参考等级的个数。ηb(t)为重构模型输出第b个参考等级的置信度。

经过重构后的监测信息可以替换故障传感器的监测信息，进而能够确保飞行器控制系统按照时序工作指令正常工作。

1.3 模型稳定性分析

惯导系统故障诊断与重构模型稳定表示监测信息受环境干扰、人为误操作等原因所导致的无规律、随机波动，使得监测信息中存在一定的不确定性的情况下仍然能够满足系统要求。模型稳定性分析旨在证明输入信息存在不确定性时，BRB 模型参数设置合理情况下能够保证输出误差趋向于0。假设惯导系统同一时刻仅有一个传感器发生故障，仅考虑了加速度计性能下降这类非致命性故障下的诊断与重构，暂未考虑加速度计、陀螺仪等传感器本身安装误差、标度因数误差等造成的误报。为此，本节对基于BRB 所构建的惯导系统故障诊断与重构模型开展了稳定性分析。

BRB 中所使用的ER 算法如式(5)-(7)所示，其输出为β(t)。BRB 的稳定性可以表示为：

因此，通过上述推导过程可以证明，在BRB 模型设置合理的情况下，基于BRB 所构建的惯导系统故障诊断与重构框架能够在输入存在不确定性的情况下实现准确故障诊断与信息重构。

2 模型参数与更新信息量在线更新模型

2.1 模型在线更新信息调整策略

模型输出误差表示当前时刻模型对于输入信息与理想结果之间的非线性建模能力。模型输出误差增大表示当前时刻模型参数不准确，应该进一步学习调整；反之，当模型误差降低时表示当前时刻模型参数准确，后续可以适当降低学习强度。模型在线更新信息量表示用于模型在线更新的信息量，增大更新信息量能够提高建模精度，但同时会增加模型学习训练时间，降低其实时性；反之，模型建模精度降低，实时性增加。因此，做好在线更新过程中建模精度和实时性的平衡是保证所构建的在线故障诊断与重构框架性能的关键。基于此，本文设计了一种基于输出误差影响度自适应扩散的在线更新信息调整策略，通过模型输出误差影响度的自适应扩散实现对在线更新信息量的在线调整，平衡建模精度和实时性两大性能指标。

故障诊断模型与重构模型的输出结果可以表示为：

式中，ΛFDD(t)和ΛRE(t)分别为t时刻故障诊断与重构模型的误差；表示t-1时刻传感器的真实输出。

基于输出误差影响度自适应扩散的在线更新信息调整策略通过模型误差调整不同阶段历史信息的使用比例，对在线更新信息量进行动态调整。调整策略可以表示为：

式中，O(t)为t时刻模型更新所使用的信息量；Η1,Η2…ΗQ表示按照时间窗口所划分的Q个不同阶段历史信息，τ1,τ2…τQ为所对应的误差影响度自适应因子，用来调整对应阶段的历史信息使用比例，其初始值通过专家结合历史数量量、模型复杂度、建模时实行要求等给定，进而通过在线优化进行调整；Λ (t)表示模型输出误差。

2.2 模型参数优化

由于BRB 属于专家系统的一种，所构建的故障诊断与重构模型中的初始参数由专家结合其自身经验知识给定。受专家认知能力的影响，初始模型参数不一定准确，存在一定的偏差，需要通过所获得历史信息进行更新。因此，在确定在线更新信息量后，需要利用优化算法对模型参数开展学习调整。

由于BRB 模型参数具有物理意义，因此在优化过程中需要遵循一定的约束条件。故障诊断与重构模型中的待优化参数约束条件为：

式中，δi(t)和σi(t)分别为故障诊断模型和重构模型中指标的权重，θk(t)和νk(t)分别为对应两个模型中的规则权重。τ q、τmax、Q为建模过程中涉及的第q个专家的权重、专家权重的最大值和建模过程中使用专家的人数。

在优化模型中，对惯导系统故障诊断与重构的优化目标为输出误差最小，即故障诊断率最高与重构误差（Mean Square Error,MSE）最小。诊断率与重构误差计算方法分别表示为：

对于惯导系统故障诊断与重构框架中两个模型的优化目标为：

在本文中，优化算法选用了考虑投影算子的协方差矩阵自适应优化策略（Projection Covariance Matrix Adaption Evolution Strategy,P-CMA-ES），对所构建的故障诊断与重构模型参数开展学习训练[16]。

3 实验验证

为验证所提方法的有效性，本文基于某型号多表冗余惯导系统的多个加速度计故障诊断与重构开展了实验校验。

3.1 实验设置

实验是在实验室所搭建的飞行器惯导系统健康管理平台上开展。实验室所在地的初始对准重力加速度为9.8014 2m/s2，地球自转角速度设置为7.292115147 ×10-5rad/s，地球长半径设置为6378245m。惯导系统采样周期为5ms。实验过程中加速度计故障设置为恒偏差故障和漂移故障。实验过程选用了某型号装备惯导系统中三个加速度计，分别命名为A、B和C，实验过程中通过每9s 的累计脉冲信息变化量作为模型输入信息。实验过程中，通过加速度计不同的累计使用时间来区分故障与否，即性能稳定期的加速度计和长时间使用后超差的加速度计。实验共设置了四种模式，即全部正常、加速度计A故障、加速度计B故障和加速度计C故障。

3.2 故障诊断与重构模型构建

在本节实验中，三个加速度计监测数据的参考点各选择了4 个，即高（H）、稍高（SH）、中（M）和低（L），根据历史数据的分布可以进一步确定三个加速度计的所对应的参考等级，如表1 所示，表中的数据为累计脉冲量，无量纲。在故障诊断模型中，输入信息为三个加速度计的监测数据，输出为加速度计的故障情况；在故障传感器输出重构模型中，输入信息为剩余两个传感器的监测数据，输出为重构后的故障传感器输出。实验中，标准故障向量设置为：

表1 加速度计参考等级和参考值Tab.1 Reference points and value of the accelerometer

在本节实验中，J=2。

因此，根据规则的构造方式，实验中的故障诊断模型和故障加速度计输出重构模型分别有64 条和16条规则。初始故障诊断模型和三个加速度计故障下的输出重构模型的初始参数由专家结合自身经验给定，即根据规则中加速度计监测数据参考等级的组合判断当前时刻加速度计的故障状态。

3.3 模型训练与测试

实验过程中共获取了800 组数据，其中随机抽取400 组作为模型的训练数据，剩余的400 组数据作为模型的测试数据。在训练环节，全部的400 组数据用来对模型参数进行训练；在测试环节，利用本文方法开展在线训练，并通过在线更新信息调整策略对在线更新信息量进行调整。训练过程中，将400 组数据平均分成4 个时间窗口，其中误差影响度自适应因子初始设置为τ1=1，τ1=0.5，τ1=0.2和τ1=0.1。P-CAM-ES 优化算法中训练迭代次数设置为200 次。优化后的故障诊断模型和三个加速度计的输出重构模型分别如表2-5 所示。

表2 训练后的故障诊断模型Tab.2 The optimized fault diagnosis model

表3 加速度计A 输出重构模型Tab.3 Output reconstruction model for accelerometer A

表4 加速度计B 输出重构模型Tab.4 Output reconstruction model for accelerometer B

表5 加速度计C 输出重构模型Tab.5 Output reconstruction model for accelerometer C

训练后模型的故障诊断率基于式(32)计算为96.75%，输出结果如图2 所示。从图中可以看出，经过训练后的模型能够准确地对加速度计故障进行诊断，误诊断的点较少。实验重复20 次，每次实验过程中不同时刻的在线更新信息量和随机4 次实验的全过程信息量变化如图3 所示，其中训练数据量上限设置为180 组。

图2 加速度计故障诊断结果Fig.2 Fault diagnosis output of accelerometers

图3 在线更新信息量变化规律Fig.3 Online update information volume change law

从图3(a)中可以看出，在线更新信息量基本上分为了5 个阶段，不同阶段占比不同，按照调节因子的扩散程度进行阶段性调整。另外，纵向对比（如图3(b)）可以发现，训练初期对于数据量要求比较大，证明初期误差变化较大；训练后期模型参数误差进一步降低，进而对于在线更新数据量的需求有所降低。为了进一步验证所提方法的有效性，与传统的BRB 模型、模糊模型、神经网络模型开展了对比实验，其诊断率分别为97.00%、78.65%和70.20%。可以看出，相对于传统BRB 模型，本文的建模方法精度与其基本一致，但在线更新所使用的信息量有了很大程度的降低；同时，对比其他两种典型的知识驱动和数据驱动方法，建模精度分别提高了23.01%和37.82%，进而验证了所提方法的有效性。

重构模型的输出如图4 所示，从中可以看出，对于单个加速度计故障的情况下，所构建的模型可以对其进行准确重构在理想区域，误差较大的点较少。

图4 三个加速度计故障下的重构输出Fig.4 Reconstructed output of three failure accelerometers

为了进一步验证重构信息的准确性，本文通过平台开发的惯导系统导航精度计算软件，利用重构后的加速度计信息与故障状态的加速度计信息分别计算了所对应的导航精度，如图5 所示。从图中可以看出，经过重构后的加速度计监测信息使飞行器的导航精度较正常偏大，但基本与正常精度一致，保证了加速度计故障下飞行器的飞行稳定，验证了本文方法的有效性。

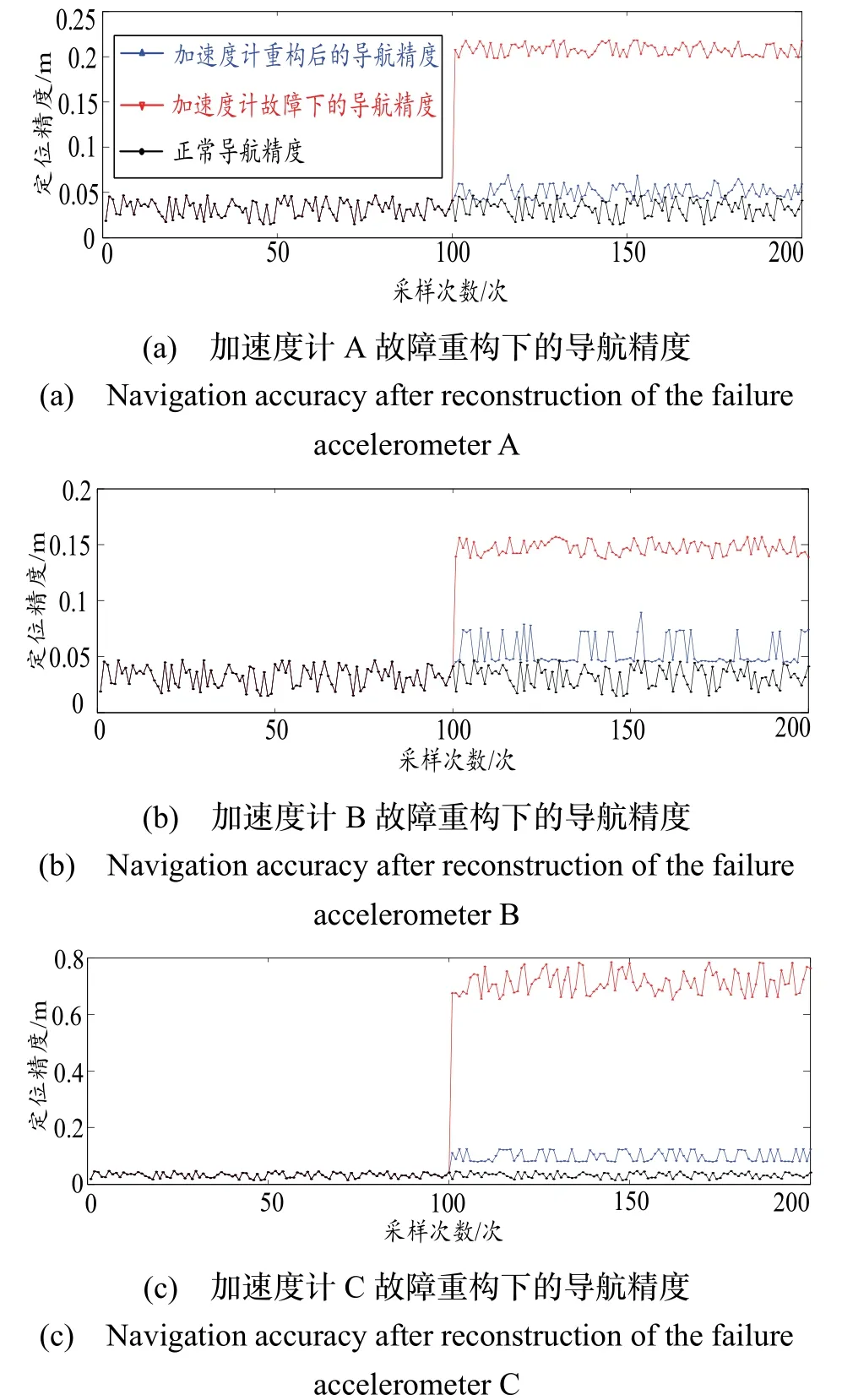
图5 故障加速度计重构后的导航精度Fig.5 Navigation accuracy after reconstruction of the failure accelerometers

4 结论

本文针对飞行器多表冗余惯导系统故障诊断与重构过程中所面临的故障状态样本缺乏、专家知识不确定和高实时性要求等难题，建立了基于BRB 多表冗余惯导系统故障诊断与重构框架，其中包含故障诊断模型和故障传感器输出重构模型，提出了一种新的基于输出误差影响度自适应扩散的在线更新信息调整策略，通过模型输出误差实现在线更新信息量的自适应动态调整，能够同时兼顾建模过程中的实时性与精度。

为验证本文方法的有效性，在某型号惯导系统加速度计中开展了应用研究，实验结果表明故障诊断精度为96.75%，同时所使用的数据量能够根据建模精度进行实时调整。