基于纠缠数态和奇偶校验的光纤陀螺仪相位测量性能分析

惠 俊，柴洪洲，杜祯强

（信息工程大学，郑州 450001）

现代光学陀螺仪是一种能够精确确定运动物体方位的仪器，在惯性导航[1,2]、精密测量[3]、测地学[4]等领域有着广阔的应用前景。光纤陀螺仪作为一种基于Sagnac 效应的新型角速率传感器，利用干涉仪中相向运动的两束光相遇时形成干涉。光纤陀螺的相位测量精度与两束相向运动的光束所包围的面积成正比，与干涉光波的波长成反比。为了提高相位测量的灵敏度，可以对测量系统进行改进或对算法进行优化[5]。改进测量系统通常采取增加光纤线圈的匝数和线圈所围半径以增大面积，或者采用波长较短的光波[6]。

量子光学的蓬勃发展也给陀螺的高精度探索开辟了新的道路[7,8]。相较于传统光纤Sagnac 干涉仪的单光输入双光输出模式，量子力学框架下的干涉仪具有双输入/双输出的特征。在传统光纤陀螺中，光按经典场处理，经典光源的相位测量精度的理论极限为散粒噪声极限（Shot Limit Noise,SNL）或标准量子极限（Standard Quantum Limit,SQL），决定了光学陀螺仪精度的理论上限[7]。利用量子信息的纠缠特性可实现测量精度的增益[9,10]。2019 年，Fink 等[11]首次提出了纠缠光子陀螺，利用双光子纠缠态实现了德布罗意波长的减半，其实验结果突破了标准量子极限。张桂才等[12]研究了基于最大纠缠态（NOON 态）的光子纠缠光纤陀螺仪的相位灵敏度，理论上，相对散粒噪声极限可提高倍（N为多光子纠缠态的光子数量）。无损条件下，对于NOON 态而言，总光子数为2N的两束光通过Sagnac 干涉仪后，相移的测量不确定度可达到海森堡极限σφHL=1/2N[13]。虽然具有最大纠缠增益，但大量研究表明，NOON 态在实际环境中易受到干扰，其纠缠性能将被严重削弱，导致最终陀螺仪测量精度的增益有限，且多光子NOON 态也不能直接作为陀螺仪的输入态[14]。而纠缠数态输入则对实际环境噪声具有更好的鲁棒性，同时可在双输入端口直接注入纠缠数态。

对于光纤陀螺仪输出端的测量，较为成熟的纠缠测量方案包括光强差检测以及奇偶校验测量[15]。考虑到双输出的量子陀螺仪光学结构，如果两个输出端的光子数相同，那么光强差结果为0，此时光强差测量结果对相位参数不敏感，无法实现对光纤陀螺仪的相位估计[16]。而利用奇偶校验测量方案不仅能实现纠缠数态的测量，同时可实现对光强差测量方案的改进。

综上所述，本文提出了采用双模纠缠光子数态作为光纤陀螺仪的输入，并阐述了基于纠缠光子数态光纤陀螺仪的基本原理。同时，针对光强差测量存在的不足，提出了针对其中一条光路的输出端进行奇偶校验的测量方案。基于无损传播模型，本文首次推导了双模纠缠光子数态（孪生数态）光纤陀螺仪的相位估计误差公式。在输入相同光子数条件下，将其与经典相干态和最大纠缠NOON 态输入的光纤陀螺仪相位估值精度的极限进行了对比，并展示了在特定情形下运用奇偶校验方法来提高纠缠光纤陀螺仪测量精度的优越性。

1 Sagnac 干涉效应

1.1 经典光纤Saganc 干涉仪

光纤陀螺作为一种重要的传感器，是当前的精密测量物理技术之一。它与基于经典力学的机械陀螺一样，可用于测量运载体相对于惯性空间的旋转角速度。V.Vali 和R.Shorthill 构建的Sagnac 干涉仪由光纤线圈构成闭合环路，如图1 所示。在一个半径为R，面积为S的圆环光纤中，由同一光源发出的光被半反射半透射分束器BS 分成两束，分别沿顺时针光路LCW和逆时针光路LCCW传播，之后两束光在分束器BS 处再次相遇并产生干涉，干涉光的强度由输出端的探测器检测。在干涉仪静止的时候，两者相遇无相位差，LCW=LCCW，干涉条纹的中心为（零级）明纹；而当干涉仪以角速度Ω沿其法线方向顺时针旋转时，在输出端可以检测到干涉光强的变化，这种由干涉仪旋转引起的相位变化称为Sagnac 相移φ。在RΩ≪c的条件下，它与旋转角速率Ω的关系为[17]：

式中，λ为旋转参考系中的光波波长；L为光纤长度；R为光纤环的半径；c为真空中的光速（如图1）。所以，Sagnac 效应经常被用来测量某一惯性参考系的旋转角速度Ω，由式(1)可知，为了提高干涉仪的角速度测量精度，可以增大圆环的面积S（增大半径R）或者增加光纤匝数M（增加长度L）。除此以外，可以通过量子技术增强相位测量的灵敏度从而实现更加精密的角速度测量[13]。

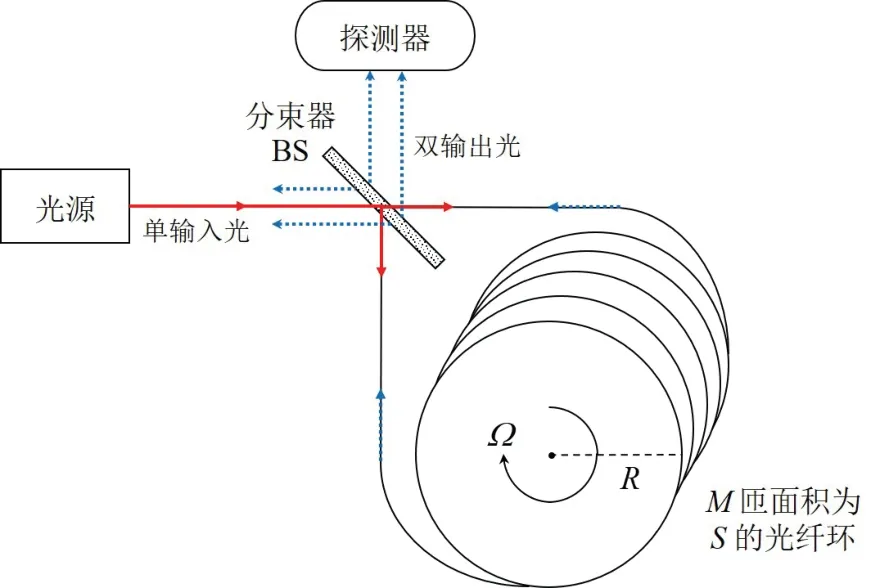
图1 经典光纤Sagnac 干涉仪示意图Fig.1 Diagram of the classic fiber Sagnac interferometer

经典Sagnac 干涉仪为单输入/双输出模式，它由一个50:50 分束器和一个光纤线圈组成。输出端可采用不同的光学测量方案，最终实现环路中的Sagnac相位估计。通常的测量方法是对两个输出端口的光强差进行测量。理想情况下，两个输出端口的光强测量结果分别为[12]：

1.2 光纤Saganc 干涉仪的量子力学描述

在量子Sagnac 干涉仪中，真空场总是存在的，即使没有光进入分束器的另一个端口，真空场也会从这个端口进入，因而干涉仪实际应为双输入/双输出模式。光纤环Sagnac 干涉仪与分立形式的Sagnac 干涉仪的光学变换过程是等价的。下面对分立形式的Sagnac 干涉过程进行量子化描述，如图2 所示。

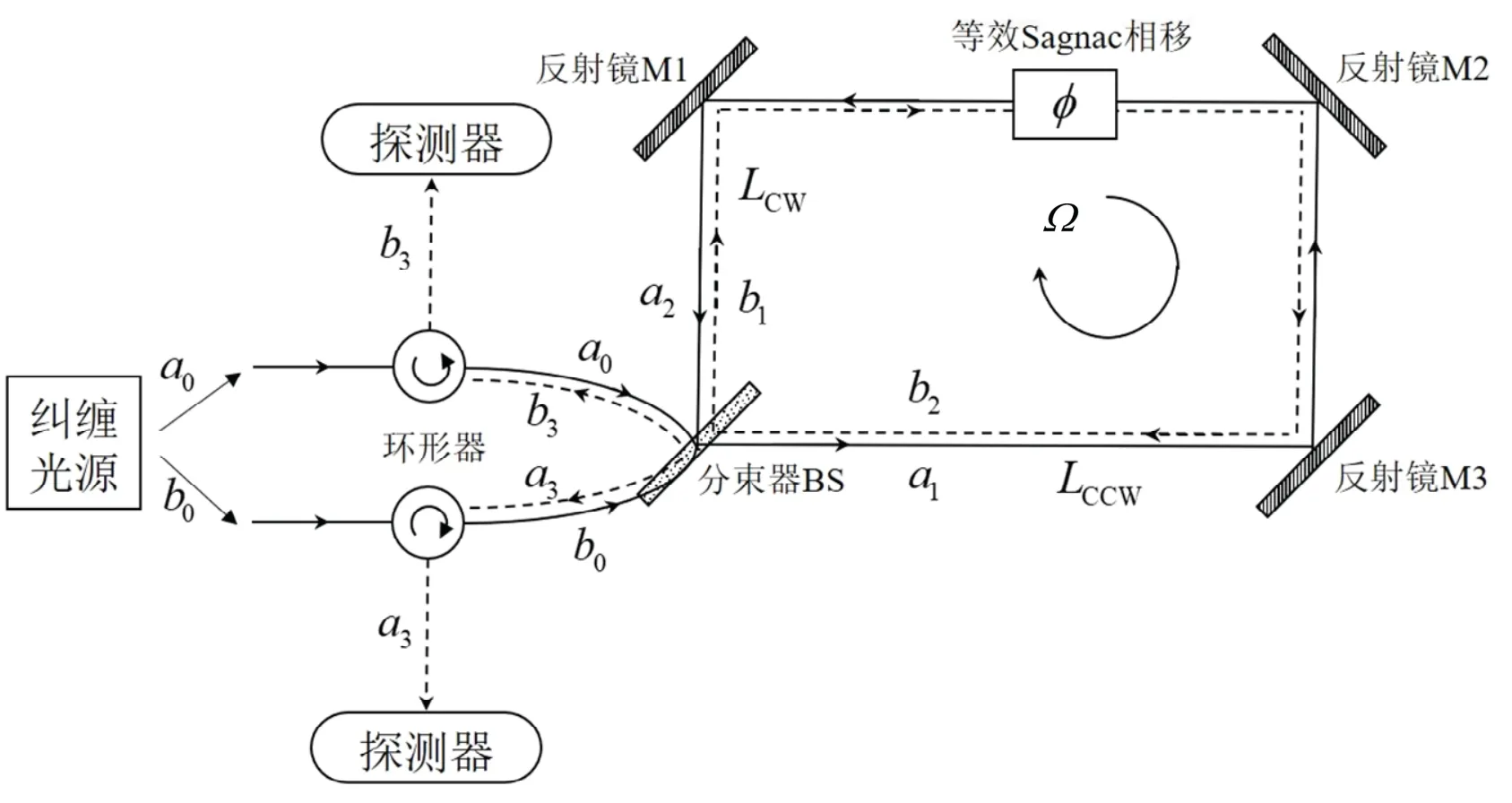
图2 分立形式的Sagnac 干涉仪Fig.2 Discrete form of Sagnac interferometer

2 基于纠缠光子数态的光纤陀螺仪

2.1 双模纠缠光纤陀螺仪的输出态

考虑运载体做旋转运动导致Sagnac 相移，假定这一相位移动发生在b模式中，则第二次通过分束器之前的量子态为：

式中，k∈[0,N]。

2.2 奇偶校验方案与相位测量精度估计

本文设计的光纤陀螺仪干涉系统中采用半反半透分束器，即认为分束器的分光比为50:50，且无能量损耗。为了避免入射到光纤环中的光返回光源，从而对入射光路径造成干扰，实验中采用环形器代替耦合器。环形器作为一种多输入输出的光学器件，主要用于光的传输路径选择，其结构图如图3 所示。从端口1 输入的光仅从端口2 输出，从端口2 输入的光仅从端口3 输出，并假定传输过程没有光子损失。

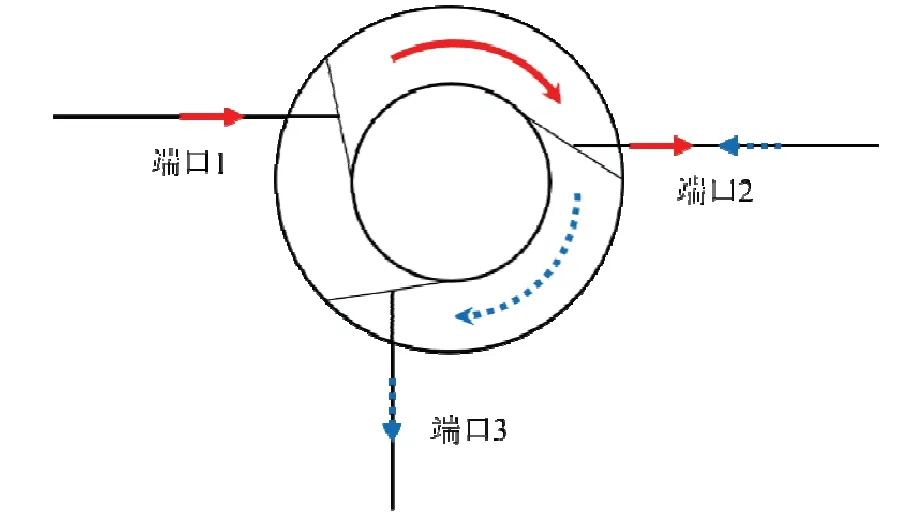
图3 光纤环形器结构图Fig.3 Structure diagram of optical fiber circulator

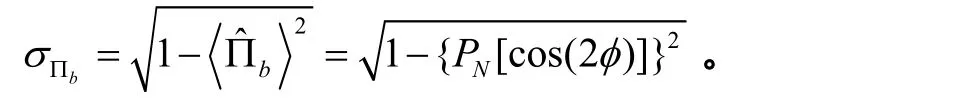
3 对比和仿真

3.1 纠缠光子数态与NOON 态的比较

在纠缠光子数态光纤Sagnac 干涉仪中，最优的输入态为NOON 态，通过光强差测量，NOON 态可以实现的相位测量精度为1/N。对于总光子数为2N的NOON 态输入，经过Sagnac 相移φ有：

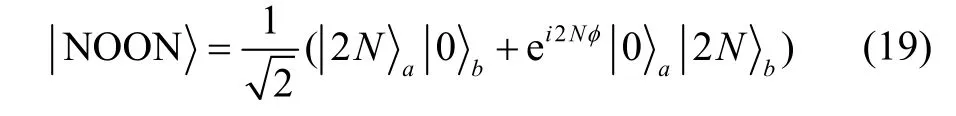
当N＞ 1时，仅通过Sagnac 干涉仪的光学变换难以得到最大纠缠NOON 态，多光子NOON 态的制备必然要更改Sagnac 光路结构，增加了干涉仪的复杂程度。鉴于量子Sagnac 干涉仪初始输入的双模输入特征，可以在两个输入端口输入纠缠光子数态，从而在现有光路的基础上实现干涉仪相位测量精度的提高。本文以孪生数态输入为例，即两个输入端口输入的光子个数相同（对于总光子数为 2N的孪生数态，其双模纠缠光子数态的粒子数统计分布满足离散反正弦律，故又称之为反正弦态），可将具有相同总光子数的孪生数态与具有最大纠缠性质的NOON态统计分布结果PNOON(2k,2N-2k)=(δk,0+δk,N)/2（δi,j为狄拉克符号，下标不等为0，相等为1）作一比较，如图4 所示。

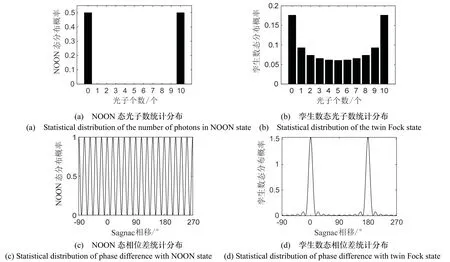
图4 双模纠缠光子数态与NOON 态的粒子数与相位统计分布（总光子数2N=20）Fig.4 Statistical distribution of the number and phase of the two-mode entangled Fock state and NOON state (total photon number of 2N=20)

当2N= 2时，由式(19)可知，孪生数态在第二次通过分束器之前，恰好转换为最大纠缠NOON 态，由标准测量理论知，对其进行光强差测量，将无法获得符合计数结果（光子数差为零），从而无法估计得到相位估计。若在输出端进行奇偶校验测量，同样取2N= 2，则由式(16)知输入孪生数态经过Sagnac干涉仪并最终由奇偶校验测量结果得到的统计均值为：

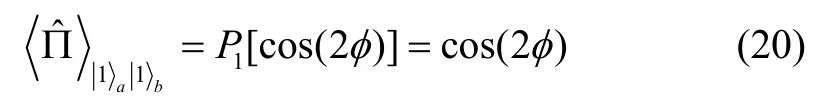
由式(15)知，奇偶校验测量的标准差为：

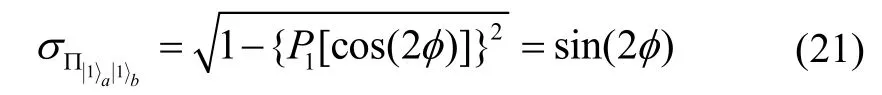
由误差传播公式（式(17)）知，相位测量的标准差为：

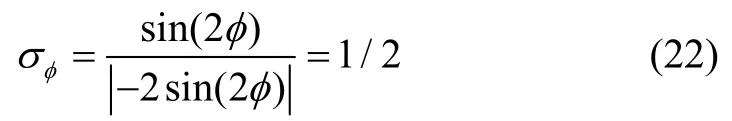
显然，这一结果达到了总光子数为2N= 2的海森堡极限=1/2N=1/2。由此可见，N = 1时的孪生数态输入经过光纤Sagnac 干涉仪制备成了NOON 态，表明奇偶校验方案完全适用于NOON 态的测量，且同样能达到纠缠光纤陀螺仪相位测量的海森堡极限。

图5 给出了相同光子数条件下（2N= 20）的相干态粒子数统计分布与相位统计分布结果。将其与图4 对比可以发现，由于光子的纠缠效应，使得纠缠数态的光子统计分布和相位统计分布发生了改变，NOON 态作为最大纠缠态输入，对光纤陀螺仪的输出增益性能最强。NOON 态输入的Sagnac 相移分布呈谐波振荡特征，其峰谷之间的距离要小于相干态输入；而孪生数态输入时，虽然由于纠缠度较低，由图4(d)中可见仅有由相位差π 隔开的两个尖峰，然而随着总光子数的增加，其峰谷距离将趋于NOON 态输入的情形。因此，对于某些特定的光子数态输入，光子的相位分布仍然可以进一步压缩，这就类似于利用量子光场的压缩特性，在某些有用的窗口内可以减少场的正交波动，从而打破测量的标准量子极限，提升相位估计的精度。

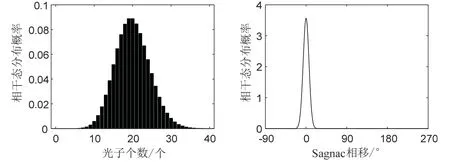
图5 相干态的粒子数与相位统计分布（总光子数2N=20）Fig.5 Statistical distribution of the number and phase of ccoherent state (total photon number of 2N=20)

3.2 不同纠缠输入态与相位测量的精度估计

除了利用量子压缩特性，利用量子纠缠同样可实现测量精度的增益。无损条件下，对于最大纠缠态（NOON 态）而言，总光子数为2N的两束光第二次通过分束器BS 后，相对相位（相移）的测量不确定度可达到海森堡极限=1/2N。虽然，NOON 态具有最大的纠缠特性，最有利于实现相位的高精度测量，但当输入端的总光子数2N＞ 2时，利用现有的Sagnac 干涉仪无法直接输入最大纠缠NOON 态，通过非线性或组合光路结构制备NOON 态无疑增加了实际应用的难度。即便制备得了NOON 态，在某些情况下，还可能出现光子数差为0 的情况，也就是说，当计算两个输出端口的光子数平均值时，其结果相等且不依赖于Sagnac 相移φ，因此在探测器的两个输出端口进行光强差探测时无法得到符合计数，从而无法通过误差传递公式对Sagnac 相位进行估计，导致方法失效。此时便可采取奇偶校验方案，而干涉仪的初始输入态只需输入纠缠光子数态即可（不一定是最大纠缠态），以双模输入光子数相同的孪生数态为例，进一步考察由奇偶校验测量结果所得到的相位估值精度。取2N= 4，则由式(16)(17)(18)可知，相位测量的标准差为：

通过上述分析，所提方法能够增强光纤陀螺仪Sagnac 相位输出精度。具体地，以光纤陀螺为例，讨论该方法对陀螺性能指标的改善。在光纤陀螺仪中灵敏度检测极限，即可测量的最小角速度，是一项极为重要的指标。通常，以能检测到的最高相位灵敏度对应为最小可测角速度：

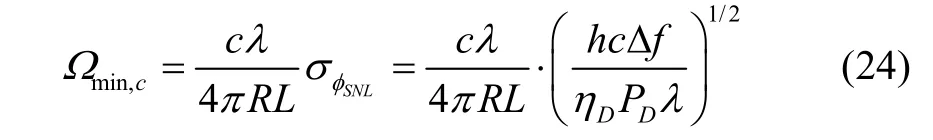
式中，h为普朗克常数，c为光速，Δf为信号测量的带宽，η D为探测器的量子效率，PD为探测器接收的光功率。对于一个波长λ=1550nm、光纤长度L=5km、线圈半径R=0.1m、探测器量子效率ηD=0.9、信号带宽Δf=0.01Hz、光功率PD=10μW的光纤陀螺，最小可测角速度为1.9 ×10-4°/h。

当采用文中方法时，相位输出灵敏度的关系为Ωmin,twin=σφtwin/σφSQL·Ωmin,c≈ 1.1 ×10-4°/h。随着输入总光子数N的增大，光纤陀螺仪的灵敏度将逐渐达到海森堡极限。由于光纤陀螺仪相位测量的灵敏度与平均输入光子数成正比关系增长，因此增加输入光子数也能增加干涉灵敏度，但基于奇偶校验方法的纠缠数态测量方案随着光功率的增加，灵敏度的增加会更快。如图6 所示，当输入总光子数仅仅增加到2N=100时，光纤陀螺的最小可测角速度相对于传统方案所能达到的最高精度就提高了一个数量级。

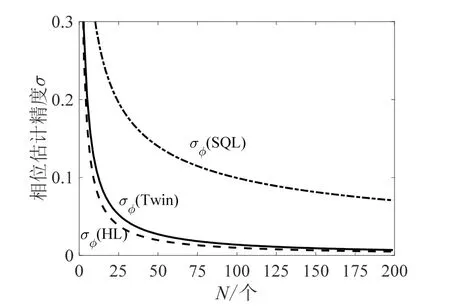
图6 不同输入态的相位估值精度随总光子数N的变化曲线Fig.6 Variation curve of the phase estimation accuracy of different input states with N photons

表1 给出了经典相干态和NOON 态、纠缠光子数态输入的量子光纤陀螺仪得到的相位检测灵敏度对比。可以看出，经典相干态在理想条件下仅能达到标准量子极限，最大纠缠NOON 态突破了散粒噪声极限，并可达到海森堡极限；而利用光强差测量方案在某些情况下无法获得相位估值。对于一般纠缠光子数态的二阶符合计数虽然存在Sagnac 相位φ的信息，但因为并非所有的输出态都对二阶符合计数有贡献，存在一个固有效率或概率，因此基于光强差测量未能突破标准量子噪声极限；如果采用奇偶校验方案，则对上述情况均能有效处理，获得相位估值精度的提高，对于NOON 态输入的测量结果可达到海森堡极限，而对于一般的纠缠光子数态输入的测量结果随着总光子数N的增大渐进达到海森堡极限。

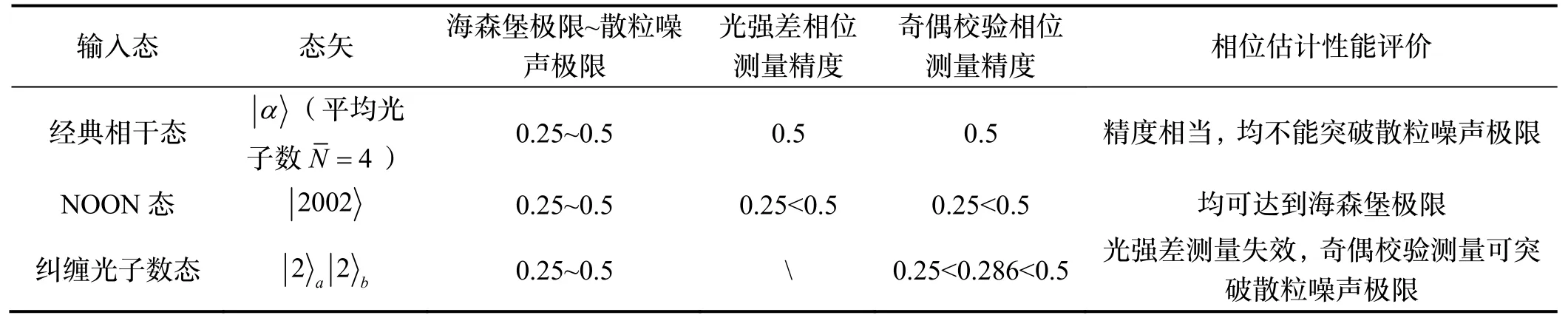
表1 不同输入态与相位估值精度对比Tab.1 Comparison of different input states and phase estimation accuracy

4 结论

基于光子纠缠光纤陀螺的双输入/双输出模式，仔细讨论了光纤陀螺仪的量子描述框架，设计了一种采用双环形器进行奇偶性探测的光路结构。通过对纠缠光子数态光纤陀螺仪测量原理的考察，发现当输出态的光子数差算符为0 时，标准光强差测量方法将失效，针对光强差测量方案存在的不足，提出了对其中一条光路的输出端进行奇偶性检验的测量方案。此外，本文基于无损传播模型，首次推导了一种基于双模纠缠光子数态的光纤陀螺仪相位估计误差公式。在相同输入光子数条件下，将其与经典相干态和最大纠缠NOON态输入的光纤陀螺仪相位测量精度的极限进行了对比，并展示了特定情况下利用奇偶校验方法来提高纠缠光纤陀螺仪测量精度的优越性。分析表明，基于纠缠光子数态输入的光纤陀螺仪虽然不能达到海森堡极限，但将随着N的增大不断趋于海森堡极限。对于输入量子态的优化选择以及输出态优化测量方案仍然需要深入探讨。此外，光子纠缠陀螺仪的研制还需要考虑光子传输的损耗特性以及退相干的影响等问题，依然有待进一步研究。