桥梁抗震设计中的结构动力学理论及计算分析

杨茂召

（招商局重庆交通科研设计院有限公司，重庆 212000）

一、工程概况

该项目的施工范围为k0+900～k13+600、k27+400～k46+800,项目内需要建设15座桥梁，桥梁的总长度设计为17.39km，桥梁的跨径主要是分为三种规格：20m、30m、40m。其中20m跨径的桥梁设计为预制装配式箱梁，30m、40m跨径的桥梁设计为预制装配式T梁，桥梁下部结构形式主要是两种不同类型：三柱式桥墩与双肢矩形桥墩；结合设计图纸来看，桥台设计采用轻型肋板台。桥墩的高度最高可达到89m，桥梁的最大纵向坡度为5%。对于桥墩高度超过40m，且主跨长度为40m的T梁设计使用墩梁固结结构，这样可以在最大程度上降低地震与行车荷载对桥梁结构造成的负面影响。

结合前期勘探报告来看，桥梁所处的位置地下结构中存在泥石流堆积物、滑坡堆积物、残破积物、火山岩、变质岩、沉积岩及岩浆岩。桥梁建设沿线刚好位于欧亚板块与印度板块的衔接区域，近些年来，该区域内的底层活动较为频繁，且地震事故出现的频率比较高。结合《中国地震动参数区划图》（GB18306—2015）内容来看，该区域的地震加速度达到了0.15g，区域内的地震烈度属于是Ⅶ度，地震动反应谱特征周期为0.45s。

二、桥梁抗震设计理论分析方法

桥梁抗震设计理论知识其实就是研究地震对区域内结构物造成的动态效应，将理论知识运用在结构中的地震波来获取运动微分公式，借助运动微分公式计算出结构物在地震作用下的移动速度、加速度及位移量，而后可以获取到结构的地震响应。现阶段，国内外学术界对于桥梁抗震设计理论的研究主要是有以下几种方法：反应谱法、静力法和时程分析法。

（一）静力法

该分析方法的理论基础是以结构物与地表振动具备相同的效应，结构物受到荷载就是因地表出现振动对结构物造成的一种惯性作用力，其具体的表达式为：

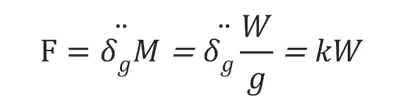
（二）反应谱法

这种分析方法是将单一自由度体系下的振动计算原理应用在多自由度体系下的地震分析场景中。通过对结构动力的特点进行分析，计算出结构各个部分的阶振，然后不同部分的阶振所面对的地震作用计算出来，最终以标准化的组合方式来计算出地震作用效应。

1.反应谱基本原理

单质点体系是由于受到地表岩层运动而形成的，单质点振动表达式为：

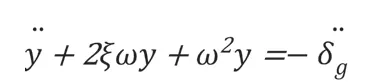
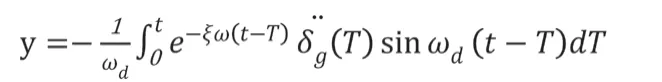
将以上表达式进行一次微分、二次微分，可以获取到单质点振子的地震加速度与相对速度反应积分表达式。通常情况下，地震的阻尼比都非常小，完全可以忽略不予以计算。故积分表达式应该是：

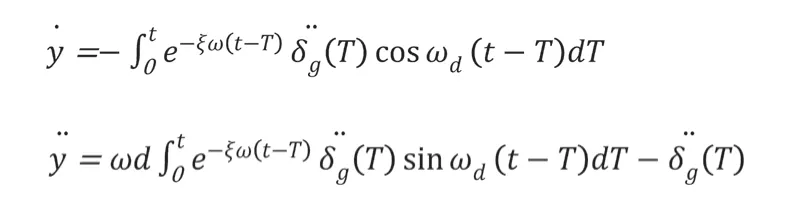
可以理解为，地震作用下形成的加速度δg属于是一个不规则的表达式，可以利用数据积分获取到地震加速度的反应曲线，多个单质点振子在相同的地震加速度δg(T)下，进一步计算可以获取到结构物的相对位移y，相对速度，绝对加速度，以此为依据计算出最大值，从而绘制出Ti为横坐标、不同阻尼比为参数的的谱曲线，这就是反应谱。

2.反应谱理论的地震力计算

反应谱分析方法比较简单，主要是有两部分组成。首先将地震反应谱函数全部整理出来，然后对结构物的振动形式进行分解。计算出在地震作用力最大的情况下，结构物抗震性能的第一步，利用单质点体系振动函数可以获取到最大地震作用力的表达式：

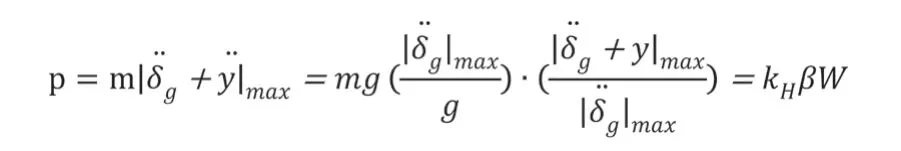
以上表达式中：g是指重力加速度；W是指总质量；定义为水平地震系数：

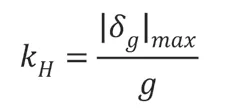
反应谱方法分析地震力的基本原理如上述表达式展示内容，在实际分析的过程中，需要涉及到两方面的影响因素：

(1)水平地震系数，简单而言就是取值。当抗震防裂度的要求不同时，那么其所对应的水平地震系数也存在一定的差异。现阶段，我国铁路工程的抗震要求为：设计烈度Ⅶ、Ⅷ、Ⅸ度的k分别取值为0.1、0.2和0.4。

(2)谱曲线的确定。不同震波带来的震波作用都存在差异性，且这种震波作用的规律比较复杂，无规可循。进一步而言，本文所使用的反应是结合既往发生的地震加速度案例记录所得，将整理所得的地震加速度数据经过特殊处理，从而形成了动力放大系数。

3.引入结构综合影响系数

反应谱研究理论是将弹性变形结构作为前提基础展开分析的，因此反应谱的分析活动具备显著的线弹性特点。结构物处于弹性变形过程中时，会逐渐转变为塑性变形状态，受力特点与结构特征会发生明显的变化，同时其对于地震的响应也会造成巨大的影响，结构处于塑性变形状态时，其能够抵抗一定程度的地震作用，在这种情况下需要纳入一个技术参数对结构的塑性变形进行分析，简单而言就是加入综合影响系数CZ。

4.反应谱组合方法

在分析地震作用时，需要对多个振型叠加计算，不同的振型所引起的地震响应效果存在较大差异，所以需要对振型进行组合，振型组合方法比较多，目前国内外使用较为频繁的方法有SRSS、CQC方法等。

（三）时程分析法

1.时程分析法概述。这种分析方法主要是对结构抗震动态化设计过程进行分析，将地表地震的加速度对结构物运动方程进行积分，由此可以获取到每一个质点随时间变化的相对位移量、速度及加速度。这种分析方法在全球范围内运用频率比较高。

2.时程分析法理论基础。这种分析方法的核心理念认为应该将结构物的运动方程纳入到地震荷载中，简单而言就是地震作用下的加速度曲线导入至结构的运动方程内，然后借助数值积分法来计算出地震作用的响应。积分过程中，将地震作用的时间划分为多个不同的时间段逐一积分，从结构运动的初始化状态作为起点，将下一段的时间节点的初始化条件作为上一个节点的结果，以此类推不断积分，直至地震作用结束。

3.时程分析法执行步骤。(1)将结构在地震作用下的运动方程划分为多个微小的时间间隔Δt；(2)若在危险时间间隔中的位移量、速度及加速度之间存在一定的关联性，可以使用特定的方法求解出结构运动的具体情况；(3)通过逐步接分的方法，以初始化条件来逐步求解出下一个时间节点的位移量、速度及加速度，从而高效地求解出结构运动方程。

三、反应谱统一计算方法

结合各国现行的抗震设计管理规标准对于反应谱设计的管理要求来看，虽然各国现行的管理规范存在一定的差异，但是设计反应谱的曲线结果是一致的，也就是结构自振周期从初始化开始缓慢增大，同时反应谱也会逐渐增大，增大至一个标准值以后，开始缓慢地降低。

结合理论研究分析来看，反应谱的曲线大致由三部分构成：上升段、平台段、下降段；其中，下降段大致可细分为两个段落；这一研究结果与各国现行的管理规范保持一致。

此外，各国现行的抗震设计管理规范中，设计反应谱还存在一定的差异之处，与理论研究存在一定的出入，其具体表现在：

上升段:以我国现行的抗震设计管理规范来看，上升段与平台段之间的连接点结构自振周期为0.1s，西方发达国家的抗震设计管理规范则是依据于现场地质条件勘察进行确定。站在理论层面来看，连接部位的周期结合不同的场地地质条件进行分类处理更具备合理性，同时与实际情况更为贴切；但是结合实践情况来看，在实际运用的过程中必然会大幅度增加工程量，常规悉尼港的结构自振周期基本上都是大于0.1s；所以本文将连接部位的周期确定为0.1s，以此减小设计活动的工作量。

平台段:以我国现行的抗震设计管理规范来看，平台段的高度基本都控制在2.25，西方发达国家的抗震设计管理规范则是将平台段的高度确定为2.5。本文将平台段的高度确定为2.25，对设计抗震存在一定的不安全影响，所以应该适当的将平台段的高度提升至2.5。

下降段:以我国现行的《公路桥梁抗震设计细则》规范来看，下降段除了一个曲线段以外，还存在两个曲线段。但是结合理论层面来看，其主要是分为两个曲线段。

第一曲线段的衰减指数为0.9，其他曲线段取值为1。结合实际情况而言，取值为1相对更为安全。

所以，结合强震反应谱理论，本文提出了以下计算公式:

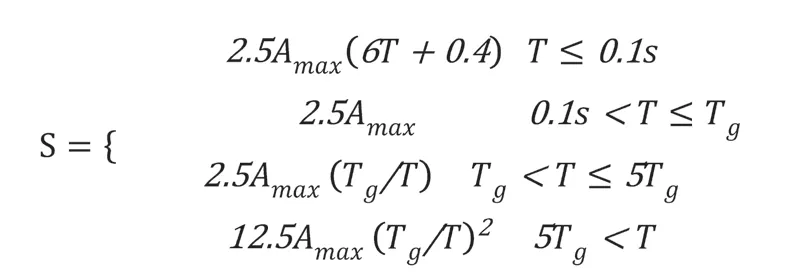
以上表达式中：Tg是指场地特征周期；Amax是指抗震设防加速度值。以Tg=0.35S为例，设计反应谱曲线如图1所示。

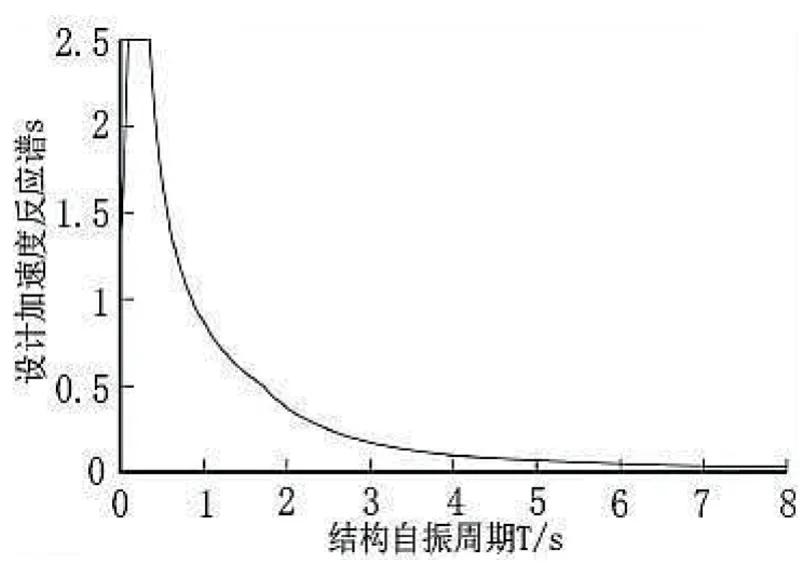
图1 本文提出的归一化设计反应谱

研究结论：设计反应谱的曲线主要可细分为3种类型：上升段、下降段、平行段；当地震结构自振周期增大以后，那么设计反应谱曲线中的下降段则可以细分为两个曲线段；此次研究过程中所提出的反应谱计算方法比较简单，且力学原理非常清晰，具有良好的应用效果。

四、结语

从桥梁地震灾害中不断总结设计经验，不断对理论基础进行优化，促使我国桥梁抗震设计理论越来越完善，本文主要是对桥梁结构抗震体系、抗震设计方法进行深入研究分析，对多种地震结构设计方法进行介绍，设计人员在实际对桥梁结构进行设计时，应该结合施工现场的地质条件、抗震级别进行设计。本文所构建出来的设计反应谱对于大跨度桥梁低自振频率结构具有一定的参考价值。