循周期之律 探自学之道
——通过培养数学“小先生”提高学生自主学习能力*
冉春莲
(西安交通大学苏州附属中学 215028)
《普通高中数学课程标准(2017年版)》指出,要提高学生从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”)[1].主动探究、自主学习有助于提高学生的“四能”.笔者在所带班级实行陶行知先生倡导的“小先生”制:以波利亚解题法为指导,鼓励一部分对数学感兴趣(不一定是成绩拔尖)的学生在老师和同学的帮助下收集素材,对学习资料进行挖掘和二次加工,以期在提高“小先生”个人水平的基础上,创造良好的学习氛围,培养学生在学习中注意前后联系、凡事寻根究底的好习惯,在培养学生独立探究能力的同时,提升学生的数学核心素养.下面以探索周期性为例介绍笔者的做法.
1 引例
在高一刚开始,笔者就给出波利亚的怎样解题四步曲,鼓励小先生们从是什么、为什么、怎么用等方面提高其研究数学问题的兴趣,尽可能地对教学内容进行拓展、挖掘,并且注意积累总结出的结论和未解决的疑问.学生在集合部分对下面的问题(引例)进行了探索:

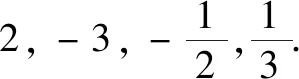

(3)还有其他的运算也具有周期性吗?学生从“运算”出发,提出了相反数、倒数、负倒数都在周期性循环,并指出A中恰好是两对负倒数——此时大多数学生还未学习周期性,但是联系初中学过的循环小数,学生很自然地提出循环.新知识迅速融入已有的知识框架,学生感觉颇有收获,体会到不能忽略任何一个知识点.
2 第一次联系
例1已知函数f(x)对任意的x都满足f(x)-2f(-x)=2x,则f(x)=.

本题通过解方程组求函数解析式,其核心在于-(-x)=x,从函数观点来看,就是函数f(x)经过若干次迭代之后可得到x,由此联想到集合部分的引例,提出

改编题的思路非常清晰,但运算量超出学生的预料.大多数学生产生了畏难情绪.在教师的鼓励下,小先生们身先士卒,攻克了运算难关,既提高了自身水平,也在班级树立了威望.
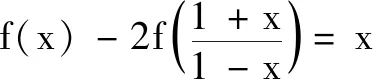
在解题反思时,学生发现解决这类题有规律性,包括运算过程可以用换元简化,所谓“为之,则难者亦易矣”.通过建立与已有知识的联系,不仅促进了学生数学运算素养的提升,也让学生对抽象函数问题的解决有了更大的信心.
3 第二次联系
例2对f(x)定义域内任一自变量的值x,若f(x+a)=-f(x)(a>0),则T=2a.
证明对f(x)定义域内任一自变量的值x,f(x+2a)=-f(x+a)=-(-f(x))=f(x),故T=2a.
通过例2,学生可以胸有成竹地给出下列结论:
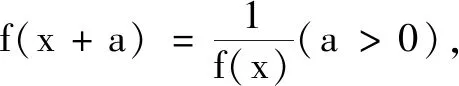

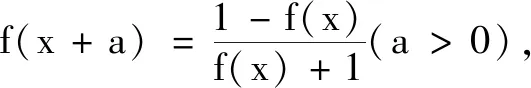



此时小先生团体已经不需要教师提醒而开始主动探索.他们联系前面所学,总结归纳发现这一类问题的本质是周期,即函数迭代的周期性,他们提出了两个问题:
第一,上述结论的证明过程都很相似,但这些高度近似“复制粘贴”的证明过程其实是个验算性说明,为什么这样形式的函数迭代之后有周期?
第二,为什么(3)(5)两个类型的周期一致,并且周期都是(4)(6)的一半?
学生讨论后的初步结果是:如果考虑函数f(x+a)=g(f(x)),(3)(5)中函数g(x)定义域和值域一致,而(4)(6)中函数g(x)定义域和值域不一致,且(3)(4)和(5)(6)刚好是互为相反数的关系.
事实果真如此吗?作为教师,笔者并没有直接指出原因,而是让学生在这里作好标记,等待后续的学习并验证.学生的归纳总结和追根究底都显示出他们的数学抽象和逻辑推理素养已有提升,而他们未得到满足的好奇心使得接下来的数学学习变得更加积极主动,更乐于探索知识之间的联系以及数学公式的来龙去脉.
4 第三次联系

解析 {an}是周期数列,本题运算并不轻松,但其特殊的形式给了学生足够的联想空间——三角函数中有大量的周期性.

学生开始思考,如何将数列与三角结合解决有关周期性的问题,如:
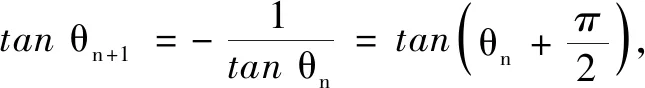


至此,学生长久以来悬而未决的疑问基本解决,并开始尝试用这个方法尽可能多地探索周期性问题.引例在必修一刚开始提出,在选择性必修二最终解决,问题解决的核心是周期性.初次出现于集合,在求函数解析式、函数周期的判断、数列周期性均有应用,问题的证明则经历了从数学运算进行验证到结合三角函数知识进行证明的过程.在这个过程中,小先生制度渐渐在班级扎根,吸引了学生靠拢和加入,同时也取得了很多成果.
在上述过程中,学生不止获得了基础知识、基本技能,提升了类比推理、归纳推理等数学思想和核心素养,更重要的是有扎根于学生的数学活动经验,让知识、技能和思想方法有迹可循.
5 结束语
用本班的一位“小先生”的话总结本文:“我们对这个问题的研究的片段,很奇妙地和很多时候数学发展的过程非常相似:数学并不一定都是先证明后使用,反而可能是发现—猜想—证明—应用—再利用—找到根本原理,最后再建立理论体系.尽管某个结论不一定会一直记得,但其中互相关联的任何一个环节都能让我很快由此及彼确认结论,而这个思维过程每次回想起来都会令人感到愉悦,感到进步的快乐.”

