利用通性通法证明2022年全国高中数学联赛平面几何题
凌惠明
(江苏省南京市金陵中学 210005)
2022年全国高中数学联赛(预赛)加试(A卷)第1题以简洁的图形、丰富的内涵,为考生能力的发挥留下了广阔的空间.本文提供几种利用通性通法来证明的方法,供大家欣赏.
1 题目

图1
(本题满分40分)如图1,在凸四边形ABCD中,∠ABC=∠ADC=90°,对角线BD上一点P满足∠APB=2∠CPD,线段AP上两点X,Y满足∠AXB=2∠ADB,∠AYD=2∠ABD.证明:BD=2XY.
2 证明
本题的证明分为两个逻辑段.
2.1 第一个逻辑段

图2
分析1由∠ABC=∠ADC=90°很容易想到A,B,C,D在以AC为直径的圆O上,由∠AXB=2∠ADB或∠AYD=2∠ABD联想到圆周角定理,可以考虑利用圆O来寻找角与角之间的关系,从而可以得到A,O,B,X四点共圆,A,O,D,Y四点共圆(图2),进而可以得到 △OXY∽△CDB.
具体证明过程可参考组委会提供的参考答案,这里不再赘述.
分析2如果没有想到利用圆周角定理来转化∠AXB=2∠ADB,可以考虑在⊙O中将两个角转化到一个三角形中,构造等腰三角形解决问题.
具体证明过程如下:

图3
如图3,取AC中点O,因为∠ABC=∠ADC=90°,所以A,B,C,D在以AC为直径的圆O上,且P,B位于AC同侧.延长AP交⊙O于点G,因为∠AXB=2∠ADB=2∠AGB=∠XGB+∠XBG,所以∠XGB=∠XBG,则XB=XG.又OG=OB,则OX⊥BG,故∠OXY=90°-∠XGB=90°-∠ADB=∠CDB.同理,∠OYX=∠CBD,故△OXY∽△CDB.
2.2 第二个逻辑段

具体证明过程可参考组委会提供的参考答案,这里不再赘述.
分析2延长AP后形成角平分线,构造三角形全等解决问题.
具体证明过程如下:

图4


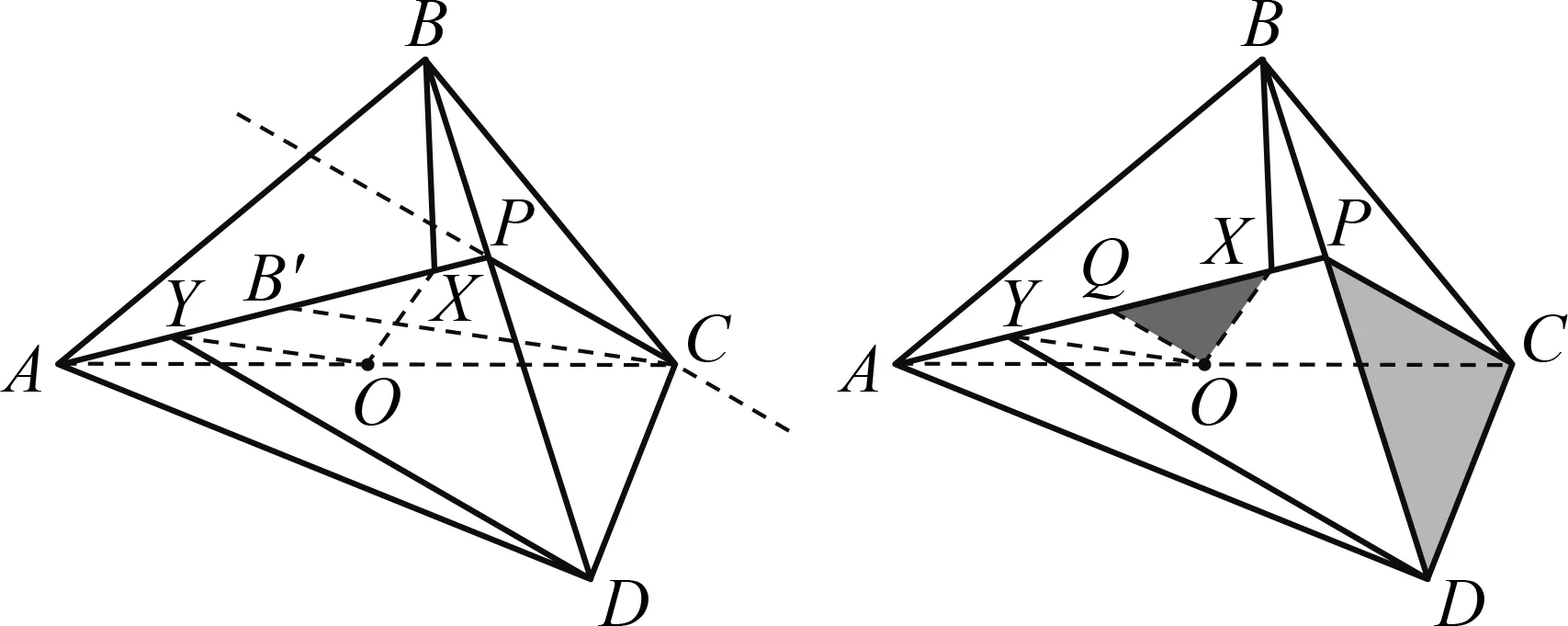
图5 图6
分析4可以利用平行寻找角与角之间的关系,结合中位线来得到相似比,具体证明过程如下.

分析5由于角与角之间的关系比较丰富,也可以考虑利用正弦定理来得到相似比,具体证明过程如下.


图7
3 结语
今年的这道平面几何题延续了最近几年联赛对学生平面几何方面的能力上的要求,突出了运用基本知识、定理和方法来思考和解决问题,是一道非常好的赛题.遗憾的是,从赛后反馈来看,仍然有不少学生面对条件∠AXB=2∠ADB和∠AYD=2∠ABD束手无策,面对条件∠APB=2∠CPD更是一片茫然.这启示我们在平时给学生训练时要更加积极地去探究解题思路的合理性,探究通性通法的运用,从而提升分析问题和解决问题的能力!

