依美构造数列，提升运算素养

俞文锐

(福建省福清华侨中学 350300)

求数列通项的方法有直接利用等差、等比公式求通项，用累加法、累乘法、待定系数法求通项，构造等差、等比数列求通项，还有利用递推公式求通项.面对如此多的题型和方法，学生显得无所适从.美无处不在，那么我们能否运用数学美将复杂数列进行变形，从而构造出特殊数列予以求解呢？下面以近年高考试题为例，设计数学美问题情境，以期提升学生的数学运算核心素养.

1 明晰运算对象，确定运算起点

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.[1]7数学运算核心素养的水平一指出：能够在熟悉的数学情境中了解运算对象，提出运算问题.[1]105由此可知明晰运算对象是展开数学运算的先决条件，教师要引导学生在熟悉的问题情境中，从不同角度进行观察，选择不同的运算对象，确定运算起点.

例1(2022年高考全国乙卷数学文科第13题)记Sn为等差数列{an}的前n项和.若2S3=3S2+6,则公差d=.

分析本题可以利用基本量方法进行求解，即将已知条件转化为d的方程.由2S3=3S2+6,得2(3a1+3d)=3(2a1+d)+6,解得d=2.

教学不应该停留于解题本身，要充分挖掘高考试题的教学价值，为此可做如下设计：

问题1 能否从题设Sn的表达式中提取出其他的信息？

问题2 能否根据统一美构造出与Sn有关的新数列？

问题3 能否利用新数列的信息求d？

通过问题1，引领学生从数量关系中抽象出运算对象，即关注Sn，发现S3与S2的系数分别为2和3，下标与系数对换，给人一种不统一的感觉.

在上述的活动中，学生经历了从数量关系中抽象出运算对象、从数学美的角度构造运算对象、根据运算对象确定运算起点的认知过程，从中使得数学抽象、数学运算等核心素养获得提升.

2 探索运算思路，把握知识本质

数学运算核心素养水平一要求：能够在熟悉的数学情境中，根据问题的特征形成合适的运算思路，解决问题.[1]105数学运算不是盲目的，往往需要学生观察数与式的结构特征，展开丰富的联想，通过合理的构造，进行严谨的逻辑推理，获得合适的运算思路.

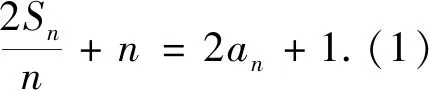
分析本题已知条件中Sn与an纠缠，要研究an必须消去一个变量，为此可做如下设计：

问题1 能否根据简洁美对已知条件进行化简并获得Sn的表达式？

问题2 能否根据对称美对化简的结果进行变形？

问题3 能否构造出新数列，并利用新数列对原问题进行求解？

3 选择运算方法，完善学生认知

数学运算的核心是思维，解题中应强化对运算思路和方法的分析，使学生逐步理解运算是一种逻辑推理，在面对与学过的知识有关联的数学命题时，能够通过对其条件与结论的分析，探索运算的思路，选择合适的运算方法，体会程序思想的意义和作用.

本题的问题情境对学生而言不熟悉，基于高考考查目标要求，结合必备知识和关键能力设计如下问题：

问题1 能否根据等差数列的定义获得Sn与an的关系式？

问题2 能否将关系式中的Sn转化为an？

问题3 能否构造出与an有关的新数列？

在上述的活动中，学生对于较复杂的数学问题，能够通过结构与变量的和谐统一美，对式子进行变形构造，得到完美统一的关系式，从而得到常数列.该活动让学生进一步认识到数学美的威力，促进学生将新知识同化到已有的数学认知结构中，从而使数学认知结构得到进一步的发展.

4 变换运算背景，累积活动经验

数学运算核心素养和数学思维的提升不能仅仅满足于熟悉情境下的模仿与记忆，为了提高学生在综合情境中把问题转化为运算问题的能力，教师需要不断变换运算背景，提高学生的应变能力.

例4(2021八省联考第17题)已知各项均为正数的数列{an}满足an+2=2an+1+3an．

(1)证明数列{an+an+1}为等比数列；

分析 (1)略；

(2)由(1)得an+an+1=2·3n-1，根据求通项公式的经验，移项得an+1=-an+2·3n-1，此时发现an+1，an的系数不含n，还能通过适当的变形化成对称统一的结构吗？

在上述的活动中，学生从综合的运算背景中，能够通过构建过渡性的命题，探索论证的途径，解决问题，并会用严谨的数学语言表达论证过程，感悟数学之美，积累依美构造数列的经验.

5 结语

依美理解运算对象，依美探究运算思路，依美选择运算方法，依美求得运算结果，学生在教师设置的问题情境中，感受到数列通项求解过程中结构变量的对称美、统一美，自觉地用美来解决递推数列问题，从而实现数学美在递推数列问题中的知行合一，同时累积了求解递推数列通项公式的基本活动经验，学会用美的眼光看问题，培养和发展数学运算核心素养.