单元整体视角下的高中数学概念复习教学的实践与探索
——以“解三角形”一轮概念复习教学为例*
吴万征
(江苏省句容高级中学 212400)
1 学情分析
本次教学对象是四星级高中的高三物化生组合实验班学生,基础较好,有较强的自主学习能力、运算能力和综合运用知识解决问题的能力.
2 考点解读及教学目标
纵观近几年高考数学全国卷,解三角形是重点考查内容之一,其本质是在三角形内蕴方程的基础上将试题设定的条件与内蕴方程建立联系,求得三角形部分度量关系[1].解三角形或以选择题、填空题的形式出现,考查考生对三角形边角关系的理解、三角形面积公式的应用等;或以解答题的形式出现,考查三角恒等变换、正弦定理、余弦定理等知识点,考查降次、消元和换元等数学方法及数形结合、函数与方程和转化回归等数学思想,大多是中等难度试题,灵活多变,具有良好的区分度,要求考生具有一定的运算求解能力和逻辑思维能力,同时要求考生能合理选择解题方法.

教学重点 从单元整体的视角构建《解三角形》这一章的知识体系.
教学难点 (1)用余弦定理、正弦定理、射影定理结论中的两个式子推导第三个式子;(2)余弦定理与正弦定理等价性证明.
3 主要教学过程
3.1 开门见山,直奔主题
师:同学们,我们今天复习“解三角形”.

师:如何通过向量运算得出三角形的边角关系?
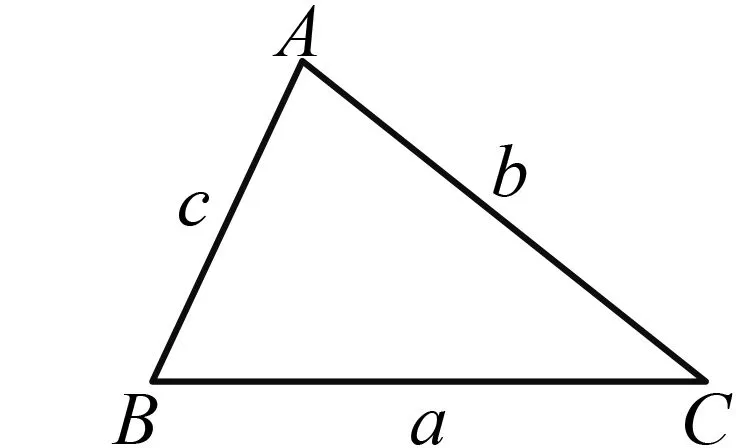
图1
师:如图1,在△ABC中,角A,B,C的对边分别为a,b,c.你的结论是——
生1:余弦定理a2=b2+c2-2bccosA.
师:你可以说说余弦定理的文字语言吗?
生1:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
师:真不错.余弦定理的符号语言呢?
生1:刚才的式子和b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
师:生1通过把向量等式两边平方,通过算两次得到余弦定理.这是向量等式数量化的结果.
问题2你还有其他证明余弦定理的方法吗?请说说证明的思路.
生2:以点B为坐标原点、BC所在直线为x轴、垂直BC的直线为y轴建立平面直角坐标系,得到A,C的坐标,用两点间距离求出线段AC,另一方面AC=b,就证得余弦定理的一个等式.其他两个同理可证.
师:用解析法把线段AC算两次得到余弦定理,把几何问题代数化.余弦定理还有其他形式吗?
师:夹角公式的用途是——
生3:一方面更方便记忆公式,另一方面可以解决已知三角形三边求三内角的问题.
师:这是余弦定理能解决的斜三角形的一类问题.余弦定理还有其他用途吗?
生3:已知两边及其夹角,求第三边及其他两角.
师:在△ABC中,角A,B,C的对边分别为a,b,c,则a2=b2+c2-2bccosA①,b2=a2+c2-2accosB②,c2=a2+b2-2abcosC③.余弦定理的这三个式子对称、轮换,非常完美.我们在学习诱导公式的时候,用两组公式可以推导第三组公式.在这里,有一个类似的问题:
问题3在余弦定理的三个式子中,取其中两个,能否推导出第三个?例如,由①②两式能否推导出③式?请思考.
生4:可以的.由①②两式可以归纳出③式是显然成立的.(生众笑)
师:请给出“显然成立”的证明.
生4:……(挠耳表示不知,生众笑)
师:此时,我们怎样分析问题?
生众:观察条件和结论.问自己两个问题:条件是什么?结论是什么?
师:波利亚的怎样解题的方法深入骨髓!条件是什么?
生众:①式和②式.
师:结论是什么?
生众:③式.
师:条件与结论之间有哪些联系?
生4:A+B+C=π.
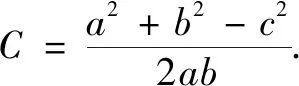

师:这样把向量等式数量化后得到一般三角形的射影定理.直角三角形的射影定理是?
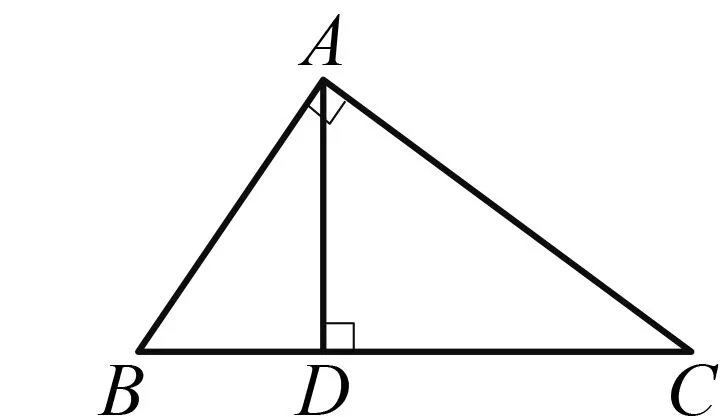
图2

师:怎么证明?
生5:用三角形相似证明.
师:在射影定理的三个式子中,取其中两个,能否推导出第三个?留作同学们课后思考.

本届黄河国际论坛的主题是“流域可持续发展及河流用水权保障”,论坛围绕主题设立流域综合管理、健康河流与环境流量、应对气候变化、流域管理工作和新技术、水管理与公众参与等五大分论坛,同时召开了12个政府间合作及国际组织相关专题会议。国际水利相关新技术、新成果、新设备展览在论坛期间并行举办。
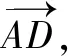
师:确实得到一个等式.和前面的余弦定理与射影定理相比,老师觉得这个等式不美,请你想一个办法,把这个式子调整得简洁美观.
生6:acos∠ADC+ccos∠BAD=bcos∠CAD.
师:等式里的∠ADC,∠BAD,∠CAD可以转为△ABC的内角吗?
生6:不可以.
师:这里的AD是边BC上的中线,可以调整一下吗?

师:为什么调整为高线后就可以得到正弦定理?
生6:调整为高线后就有两个垂直向量,它们的数量积等于零.同时得到两个直角三角形,把∠BAD和∠CAD转为它们的余角∠B和∠C.
师:大家同意他的看法吗?
生7:△ABC的形状会影响结论的.
生6:不影响,不妨设∠C最大,讨论一下∠C为锐角、直角与钝角的情况就行了.
师:如此分类讨论,正弦定理的证明思路就严谨了.你可以说说正弦定理的文字语言吗?
生6:三角形的各边与它所对角的正弦之比相等.
问题4你还有其他证明正弦定理的方法吗?请说说证明的思路.

图3
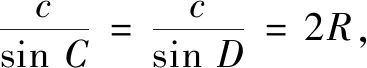
师:生8建立直角坐标系,利用三角函数的定义把三角形面积算两次证明正弦定理;生9通过三角形的外接圆,将任意三角形问题转化为直角三角形问题证明正弦定理,得到了比值为三角形外接圆的直径.正弦定理的证明方法很多,在正弦定理的三个式子中,取其中两个,能否推导出第三个?留作同学们课后思考.
师:正弦定理有哪些常用变形式?

师:请问第⑤式如何证明?
生10:大边对大角,然后用正弦定理把边关系转化为角关系.
师:在△ABC中,由A>B能推导出cosA与cosB的大小关系吗?
生10:由余弦函数的单调性可知,在△ABC中,A>B⟺cosA 师:换成正切呢? 生10:不好判断. 师:你的知识体系很完整,点个赞! 师:正弦定理能解决斜三角形哪些问题? 生11:已知两角与任一边,求其他两边及一角;已知两边与其中一边对角,求另一边及两角. 问题5正弦定理、余弦定理、射影定理都是三角形基本要素之间的等量关系,那么它们之间有怎样的联系呢?是相互等价的吗?以正弦定理与余弦定理为例,请尝试. 师:条件是什么? 师:这个条件有其他形式吗? 生12:a=2RsinA,b=2RsinB,c=2RsinC. 师:目标是什么? 生12:证明余弦定理a2=b2+c2-2bccosA,另外两个式子同理可证. 师:目标有其他表达形式吗? 师:目标与条件有什么关系? 生12:可以把条件代入目标,化简整理. 师:思路很清晰,用证明等式的想法,化繁为简.请板书你的证明过程,其他同学在稿纸上证明. 同理b2=a2+c2-2accosB,c2=a2+b2-2abcosC. 师:类比刚才的用正弦定理证明余弦定理,请由余弦定理证明正弦定理. 生13:不太好证明. 师:我们一起分析,条件是什么? 生13:△ABC满足余弦定理a2=b2+c2-2bccosA,b2=a2+c2-2accosB,c2=a2+b2-2abcosC. 师:目标是什么? 师:条件向目标转化,还是目标向条件转化? 生13:两个方向都不太好处理. 师:请观察条件和目标,它们具有怎样的结构特征? 生13:条件是三个二次的等式,目标是分子和分母都是一次的分式. 师:降幂好,还是升幂? 生13:升幂,a2sin2B=b2sin2A. 师:升幂后的目标与条件有联系吗? 生13:再转化为a2(1-cos2B)=b2(1-cos2A). 师:如何证明这个等式? 生13:即证a2cos2B-b2cos2A=a2-b2. 师:思路厘清了.请板书你的证明过程,其他同学在稿纸上证明. 生13:由余弦定理知 师:两位同学的数学基本功很强.我们在分析和解决问题的时候,经常问问自己:已知条件是什么?目标结论是什么?它们两者之间的关系是什么?已知条件可以转化吗?目标结论可以转化吗?转化后,它们两者之间的关系是什么? 问题6对于解三角形,你还有补充吗? 师:你可以证明吗? 图4 图5 生15:结合条件“AD是∠BAC的平分线”,分别在△ABD和△ACD中用正弦定理,然后两式相比就得证. 师:这是三角形的内角平分线定理.外角平分线定理呢? 师:你可以证明吗? 生16:结合条件“AM是BC边上的中线”,分别在△ABM和△ACM中用余弦定理的夹角公式,然后两式相加就得证. 师:三位同学补充了三角形的面积公式、三角形角平分线定理和中线长公式三个常用的结论,并用算两次的算法思想给出了相应的证明. 2011年高考数学陕西卷文理科第18题:叙述并证明余弦定理.此题考试结果很不理想,满分12分的题,平均分只有5.43分,而且,“叙述”定理部分可以得4分,可见“证明”定理部分几乎没有得分[2].这是30年后再次考查余弦定理的证明,而答案就在课本上.这就提醒我们一轮复习要紧扣课本:紧扣概念、定义、定理、公式等发生发展的过程;紧扣课本经典例题、练习和习题所蕴含的解题方法和数学思想,穿珠成串. 本节课,在学生复习课本的基础上,笔者两节课连上,在师生、生生交流间完成解三角形知识点的复习.笔者不着急、不赶进度,给学生时间展示复习的成果,板书解答的过程.比如生6在向量等式数量化时,在等式两边点乘三角形中线所构成的向量得出等式后,笔者从等式对称美的角度,从用三角形基本要素表达的角度启发生6用三角形高线所构成的向量实现正弦定理的生成,并追问生6为什么用高线,把学生的思维“挤”出来,唤醒数学知识记忆. 概念复习课是一轮复习教学的常见课,也是基础课.笔者从教以来实践过的一轮概念复习课的模式有:当作新课带学生重新快速上一遍;带领学生简单罗列教材上的知识点;将概念的关键字删除后让学生完成概念填空;将概念融入简单习题作为前置作业由学生课前完成;布置学生自主整理章节思维导图等.如此概念复习教学,浮光掠影,都不能避免知识的碎片化,也不能促进学生在螺旋式教学中获得对概念更深层次的认识.《普通高中数学课程标准(2017年版2020年修订)》指出:关注单元知识的系统性,帮助学生理解数学的结构,增进复习的有效性,达到相应单元的“学业要求”[3]93;《中国高考评价体系》要求:对同一层面的知识、能力、素养能够横向融会贯通,形成完整的知识结构、能力结构网络[4]. 高三数学复习课时间紧、任务重、容量大、节奏快,笔者曾经一度轻概念的复习,引导学生将概念一过,随即就进入刷题讲题循环模式,期待在刷题中学会刷题.结果是笔者忙碌于各种题型的总结,疲惫于各种试卷中难题的讲解,错过了给予学生对概念,尤其是核心概念在一轮复习中深层次再理解和融会贯通的机会,致使学生在考试中遇到所谓新题一筹莫展、束手无策.实践证明:高三数学复习中,应立足单元整体,在每一个章节复习起始课上,教师加强学习方法指导,帮助学生养成良好的数学学习习惯,敢于质疑、善于思考,理解概念、把握本质,数形结合、明晰算理,厘清知识的来龙去脉,建立知识之间的关联[2].这不仅不会影响复习的进度,还会更有效地帮助学生夯实数学基础知识,拓展基本技能,深化基本思想,积累基本活动经验,有利于促进学生通过发现事物内部以及事物之间的关系和规律将知道的一系列的数学事实构建成知识体系和模型,并向更完备的方向发展,形成解题思维的固着点,让逻辑推理的数学素养落地生根,事半功倍. 本节课,笔者看似一道例题没有讲、学生一道练习没有做,实则师生交流间至少完成了8道题:余弦定理、射影定理和正弦定理的证明,余弦定理的三个式子中的两个证明第三个,正弦定理与余弦定理等价性证明,以及用正弦定理证明三角形的角平分线定理,用余弦定理推导三角形的中线长公式.笔者抓住一轮复习的契机,通过余弦定理、正弦定理和射影定理的证明建立知识之间的深层联系,并基于联系,猜想并证明正弦定理和余弦定理的等价性,发展学生的逻辑推理素养.囿于学生的接受能力,笔者没有点明余弦定理和射影定理是等价的,而余弦定理是正弦定理的充分不必要条件,它们的等价是需要正弦定理加上三角形内角和定理的.这三者的等价性的本质因素是满足定理条件的六个元素是否构成一个三角形.在重温这些经典定理的证明以及定理的应用过程中,引导学生借助向量的运算,探索三角形边长与角度的关系,反复咀嚼算两次的思想,学习应用波利亚怎样解题的解题步骤解决难题,从而落实对学生分析问题和解决问题能力以及意志品质和关键能力的培养,进而实现“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展”[3]9.3.2 互证定理,深化理解







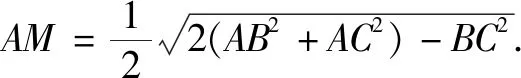
3.3 归纳小结,呼应主题

4 教学感悟
4.1 对标高考,概念复习课紧扣课本不疾而速再重现,唤醒数学知识记忆
4.2 注重生成,向量法一以贯之进行知识体系再建构,积累数学活动经验

4.3 凸显关联,着眼定理自身关系与相互关系再探究,培养逻辑推理素养

