不同影响因素下路用黄河泥沙动剪切模量和阻尼比试验及理论模型研究

王钰轲，李俊豪，邵景干，余 翔

1) 郑州大学水利科学与工程学院，郑州 450001 2) 重大基础设施检测修复技术国家地方联合工程实验室，郑州 450001 3) 水利与交通基础设施安全防护河南省协同创新中心，郑州 450001 4) 河南交院工程技术集团有限公司，郑州 450001

随着“一带一路”、“交通强国”、“黄河流域生态保护和高质量发展”等国家重大战略的推行，黄河流域相关基础设施建设与安全防护将成为重大发展领域.泥沙资源生态化利用是解决黄河泥沙问题的有效途径之一.黄河泥沙在陶瓷、板材、砖、防汛石、固化土、混凝土等建筑材料以及在土壤修复、环境治理、陶粒等方面的应用取得了诸多研究进展.高速公路的修建大都采用高填方路堤，对土的需求量巨大，而当地资源紧缺，且远距离路基填料的开采、运输需要大量的人力、物力、财力.因此，对利用黄河泥沙用作路基填料提出了需求.

有关黄河泥沙用作路基填料来研究其力学性能目前处于起步阶段，且局限于静力作用下的强度和变形特性研究，关于路用黄河泥沙的动力特性研究尚未开展.岩土材料成分和特性复杂，许多学者考虑不同因素对岩土材料的影响[1–2]，但不同因素对土的动模量和阻尼比的影响并未形成一致结论.Hardin 等[3–4]进行了大量的试验，提出固结围压、孔隙比和超固结比等因素对剪切模量和阻尼比的影响的经验公式.该公式可以应用于许多不同的土，如 Toyoura 砂[5]，Monterey0 号砂[6]，南沙珊瑚砂[7]，南海钙质砂[8]等.由于不同地区的砂土颗粒形状、级配等方面存在较大差异，其动力学特性往往各不相同，因此，有必要对黄河泥沙的动力特性进行研究.

动模量和阻尼比是描述土体动力特性的2个首要参数，现有研究表明：围压、相对密实度和试验频率对砂土的动剪切模量和阻尼比有一定的影响.国内外已有不少学者对不同地区土体的动模量和阻尼比进行了试验研究.Yasuhara等[9]认为荷载振动频率对黏性土的动力特性不产生影响；张茹等[10]、李瑞山等[11]学者认为荷载频率对砂性土的动剪切模量和阻尼比影响较小，对黏性土的影响较大；孙静和袁晓铭[12]采用共振柱试验方法，探究了固结比对砂土动剪切模量比与剪应变非线性关系的影响，认为砂土动剪切模量比随固结比的增大而增大；刘雪珠等[13]探讨了围压对剪切模量及阻尼比的影响，认为动剪切模量随固结压力增大而增大，围压对阻尼比的影响不明显；梁珂等[7]对珊瑚砂进行了动三轴试验，认为在小应变水平时，围压对阻尼比的影响较为明显，在较大应变水平时，相对密实度对阻尼比影响较为明显.

已有研究表明，砂土的最大动剪切模量主要受土体类型、孔隙比、平均有效围压的影响.Hardin和Drnevich[14]考虑围压和孔隙比对最大动剪切模量Gmax的影响，提出Hardin–Drnevich等效线性模型；Menq[15]、Saxena和 Reddy[6]考虑围压、孔隙比和不均匀系数对Gmax的影响，提出参数不同的经验公式；梁珂等[16]认为土体动力加载过程中，最大动剪切模量是不断衰退的，建立了预测珊瑚砂加载过程中最大动剪切模量的损伤模型.这些研究对于不同砂土最大动剪切模量的影响因素有不同的结论，目前尚未有系统研究黄河泥沙最大动剪切模量的影响因素文献报道.

基于此，本文采用GDS三轴仪在固结不排水条件下，对比分析围压、相对密实度、试验频率对黄河泥沙的动模量和阻尼比的影响，考虑了围压和相对密实度对黄河泥沙最大动剪切模量的影响，给出最佳拟合参数和相应经验公式.

1 试验

1.1 试验设备及土样

试验土样取自黄河中下游郑州段，沿河均匀布置多个采样点.从每个采样点提取一定量的黄河泥沙并干燥，然后用2 mm筛网筛出杂质.对黄河泥沙进行了颗粒分析试验和其他基本物理指标试验.根据颗粒分析试验结果和公路土工试验规程（JTG 3430—2020）确定黄河泥沙为细粒砂.颗粒主要物理指标见表1，级配分布曲线见图1.试验使用的仪器设备为英国GDS公司生产的GDS动态三轴试验系统，如图2所示.最大轴力为10 kN，最大荷载频率为 2 Hz，压力室最大围压为 2 MPa，适用试样尺寸为 ϕ38 mm × 76 mm.该设备满足GB28380—2012的要求，该试验系统为伺服电机控制的动三轴试验系统（DYNTTS），可开展室内试验来研究土体的动力特性，对土体的动态指标如阻尼比、动态模量、动强度等进行测试.电机控制的动三轴仪将三轴压力室和动力驱动器合为一体，从压力室底座施加轴向力和轴向变形.压力室由装有马达驱动的基座螺旋传动.当没有选择径向动力驱动器时，通过平衡锤消除动态试验对恒定围压的影响.系统可以由GDSLAB软件来控制，任一循环的数据都可以实时记录和显示出来.

表1 试验用砂物性指标Table 1 Physical properties of sand for testing

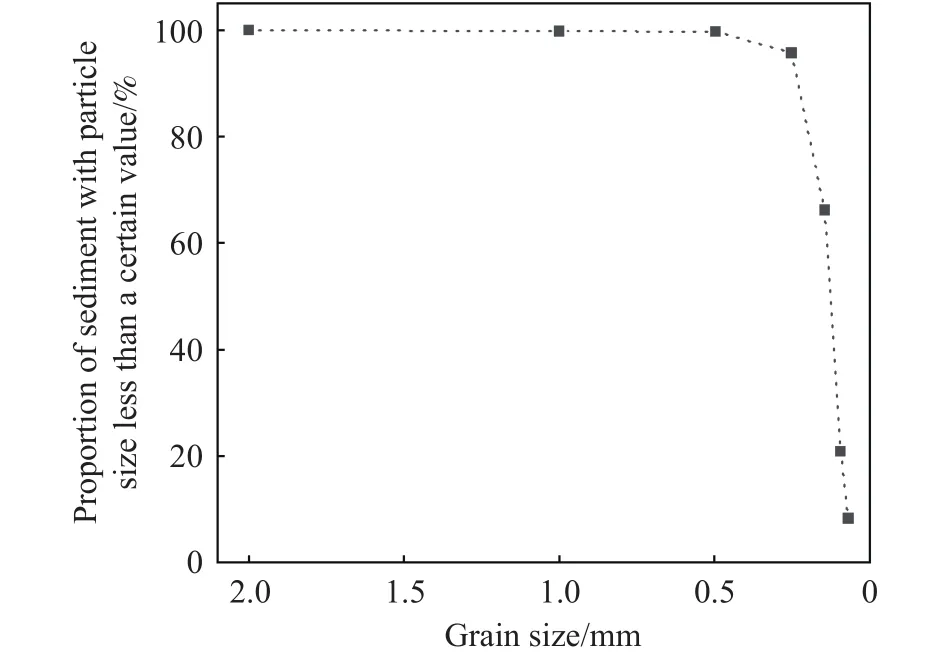
图1 黄河泥沙级配曲线Fig.1 Yellow River sediment gradation curve

图2 GDS 三轴仪Fig.2 GDS triaxial instrument

1.2 试验内容与方案

本研究全面分析围压σc、相对密实度Dr和试验频率f这3个因素对黄河泥沙的动剪切模量和阻尼比的影响，试样在压力室成样之后，先循环饱和，测得所有试样饱和参数B值达到0.95以上，试样饱和完成以后，采用等压固结.对试样进行不排水应力控制分级循环加载，轴向应力幅值逐级增大.每级荷载施加后，对试样进行一段时间的固结，再施加下一级循环荷载，依此循坏直至试件破坏.共进行了11个试样的试验，试验方案如表2所示.

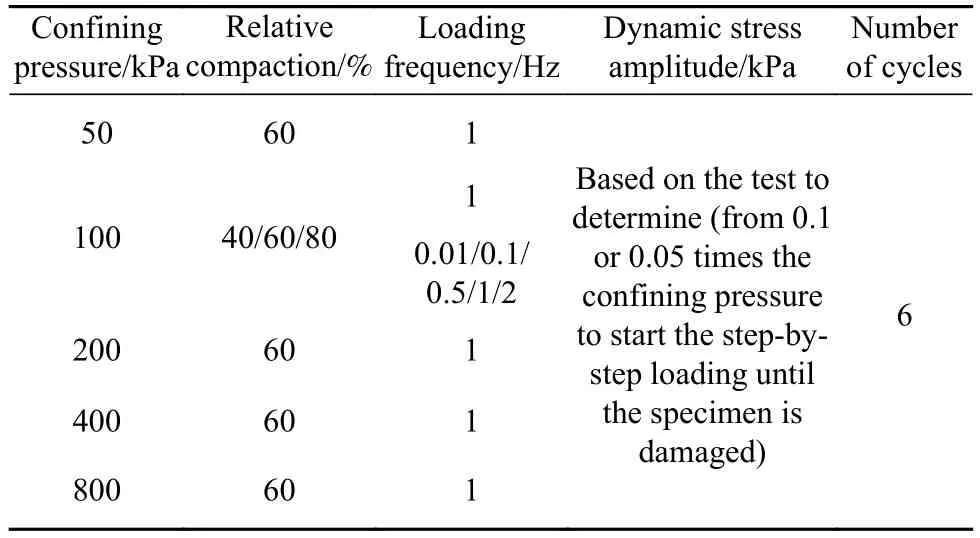
表2 试验方案Table 2 Test scheme

2 试验结果

2.1 动剪应力–动剪应变

根据已有研究结果，在动力循环荷载下，土体动剪应力–动剪应变关系 (τd–γd)具有非线性,滞后性和应变累积三个基本特性[17].以相对密实度Dr为 40%，60%，80%，试验频率 1 Hz，围压 100 kPa的工况为例，取第三圈加载所得数据绘制动剪应力–动剪应变关系曲线，由图3可知，黄河泥沙的动剪应力–动剪应变关系曲线可用HD(Hardin–Drnevich)双曲线模型来描述[14].

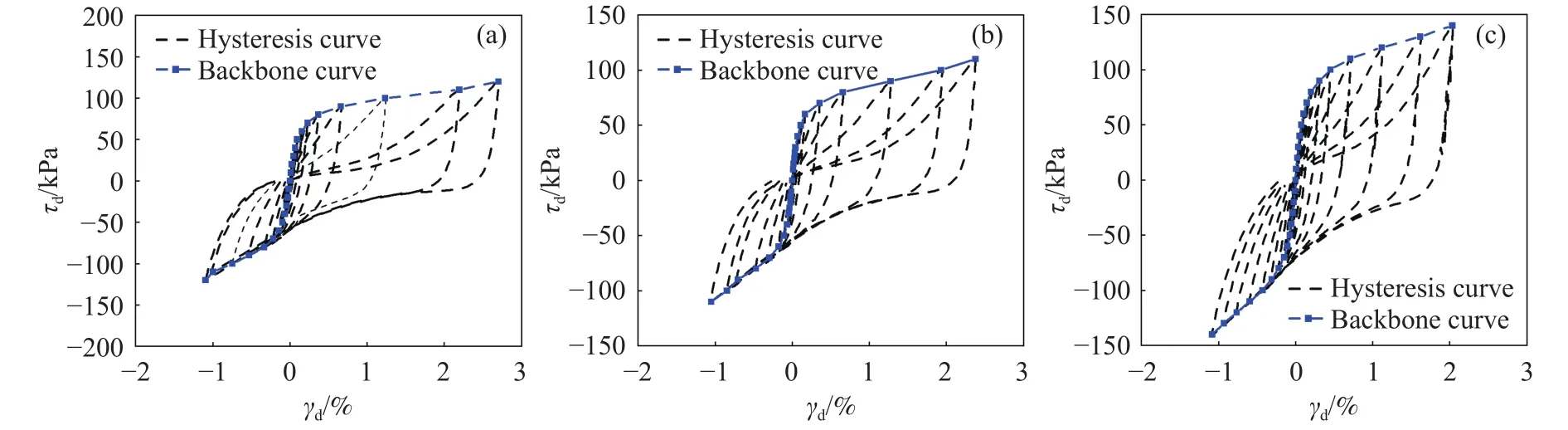
图3 黄河泥沙动剪应力–动剪应变关系曲线.(a) Dr=40%;(b) Dr=60%;(c) Dr=80%Fig.3 Dynamic shear stress–dynamic shear strain curve of Yellow River sediment: (a) Dr=40%; (b) Dr=60%; (c) Dr=80%

由图3中骨干曲线可以看出动剪应变随着动剪应力的增加呈现非线性增加的趋势.剪应变水平较小时，随着剪应力的增大，剪应变发展缓慢；当剪应变水平较大时，随着剪应力的增大，剪应变急剧增大.

不同围压及试验频率作用下黄河泥沙的动剪应力–动剪应变关系曲线如图4所示.由图4知，剪应变水平较低时，τd–γd关系曲线斜率较大.随着剪应力的不断增加，剪应变发展较为缓慢.随着剪应力的增大，应变达到一定值（γd> 0.2%）后，不同围压下的动剪应力–动剪应变关系曲线的差别越来越明显，产生相同动剪应变γd所需的剪应力τd随围压增大而增大.

在剪应变较小（γd< 0.2%）的情况下，五种试验频率下动剪应力–动剪应变曲线基本重叠，整体来看，动剪应力随着试验频率的增大而增大.在相同剪应变条件下，试验频率为0.01 Hz时的剪应力最小，试验频率为2 Hz时的剪应力最大，剪应力最大增大约为61.0%.可以得出，在一定的剪应力作用下，频率越低产生的剪应变越大.

2.2 动剪切模量

不同围压、相对密实度和试验频率下黄河泥沙动剪切模量G与剪应变γd的关系曲线如图5所示.由图5可知：不同频率、围压和相对密实度条件下，黄河泥沙的动剪切模量随剪应变的增加，呈现衰减趋势；同一应变水平下，围压越大，动剪切模量越大，当剪应变较小时，这种现象比较明显；剪应变较小（γd< 0.05%），相对密实度为 60% 的动剪切模量小于相对密实度为40%的动剪切模量，剪应变较大（γd> 0.05%），动剪切模量随相对密实度的增大而增大.循环动荷载试验频率对黄河泥沙的动剪切模量影响较小，当 0.7% <γd< 1% 时，动剪切模量随试验频率的增大有略微增大的趋势.

2.3 阻尼比 D

图6为试验所得黄河泥沙阻尼比随动剪应变幅值的变化曲线，与图5的试验条件一致.由图6可知：（1）不同频率、围压和相对密实度条件下，阻尼比随动剪应变幅的增大而增大；（2）阻尼比随围压的增大而减小，随剪应变的增加，围压的影响逐渐变小；阻尼比随相对密实度的增大而减小.频率对阻尼比的影响较为复杂，试验频率在0.01～0.1 Hz范围内，应变幅度较小时，阻尼比随试验频率增大而增大，但增大程度不明显，试验频率为0.1～2 Hz时，阻尼比随着试验频率的增大而减小；（3）相同条件下，相对密实度为40%和60%时阻尼比值在相同剪应变条件下相差较大，频率为1 Hz和2 Hz时阻尼比值在相同剪应变条件下相差较大.

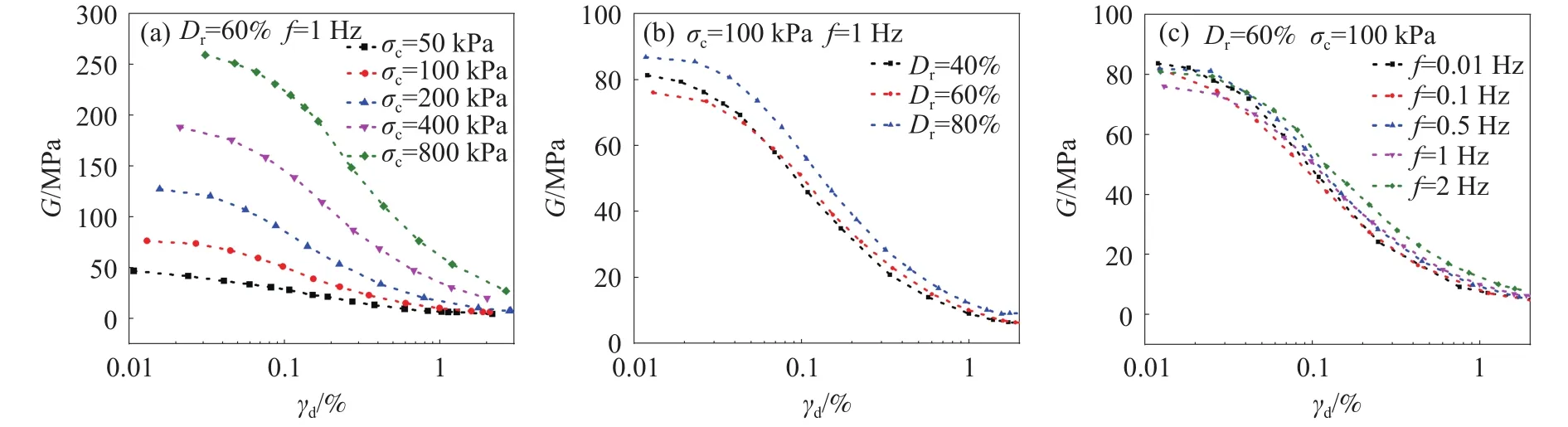
图5 不同影响因素下动剪切模量–剪应变关系曲线.（a）不同围压；（b）不同相对密实度；（c）不同频率Fig.5 Dynamic shear modulus–shear strain curve under different influencing factors: (a) different confining pressures; (b) different relative densities;(c) different frequencies

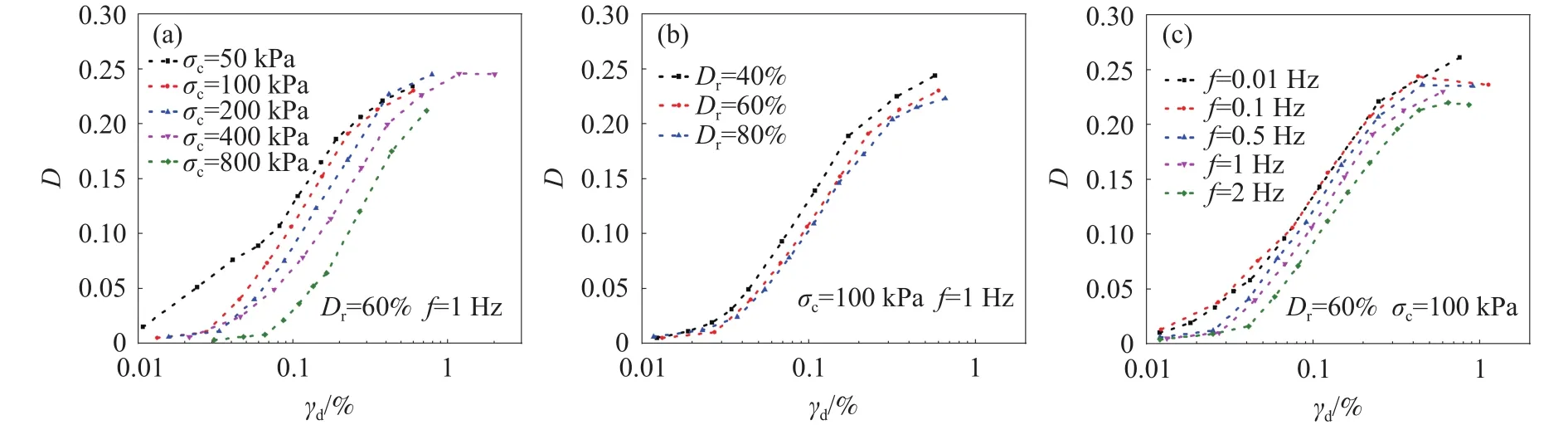
图6 不同影响因素下阻尼比–剪应变关系曲线.（a）不同围压；（b）不同相对密实度；（c）不同频率Fig.6 Different influencing factor damping ratio –shear strain curves: (a) different confining pressures; (b) different relative densities; (c) different frequencies

图7对比了围压相近条件下其他土[5,7,18–19]与黄河泥沙的D–γd关系曲线.可以发现，当D>0.14时，黄河泥沙D增长速率和丰浦砂以及粉土增长速率近乎一致，且明显大于砾石和珊瑚砂.同时黄河泥沙D曲线宽度比丰浦砂和砾石的窄，与粉土的宽度也并不完全一致.总的来看，黄河泥沙D–γd关系曲线的上下界大部分被包括在丰浦砂的上限和粉土的下界内，γd< 0.059% 时，丰浦砂和粉土的上下界均大于黄河泥沙的上下界，随着γd的增加，黄河泥沙下界开始与进入丰浦砂和粉土的范围，当γd> 0.175% 时，黄河泥沙上下界被完全包括在丰浦砂和粉土的上界范围内.此外，黄河泥沙D在γd为10–2量级时开始增加，相较于粉土和丰浦砂D开始增加的量级更大.因此，黄河泥沙D和粉土与砂土的具有相似之处，但也有一定的区别.

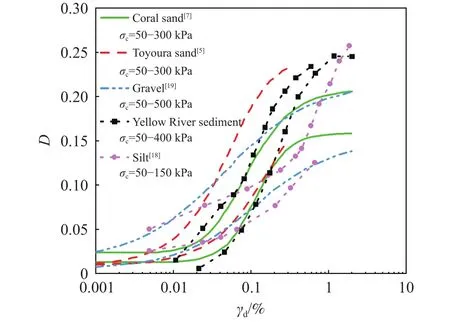
图7 不同土 D–γd 关系曲线Fig.7 D–γd curves of different soils

2.4 最大动剪切模量

土体最大动剪切模量Gmax通常取为γd= 1×10–6时的动剪切模量值.由于动三轴试验无法测试该小应变水平的动力特性，因此通过外推法确定Gmax[20–21].据此可得 1/G=m+n·γd，即G= 1/(m+n·γd)，最大动剪切模量Gmax为γd→ 0 时G= 1/(m+n·γd)中的G值，认为Gmax= 1/m.应变与动模量的拟合曲线如图8（a）所示，G–γd拟合结果见表3.

表3 G–γd 拟合结果Table 3 G–γd fitting results

以试验频率为1 Hz，相对密实度为60%，围压分别为 50、100、200、400和 800 kPa为例，图8（b）给出以lg为横坐标，lgGmax为纵坐标的关系曲线.二者呈现较好的线性关系.其中：为平均有效固结应力，=(σ1+2σ3)/3；p0为标准大气压，计算时取100 kPa用于调整量纲[22].

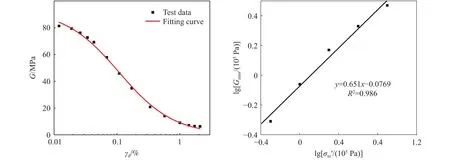
图8 (a) G–γd 拟合示意图; (b) lgGmax–lg关系拟合Fig.8 (a) G–γd fitting schematic; (b) lgGmax–lg relationship fitting

图9对比了不同砂土的Gmax值与围压的变化关系，由图9可知，Gmax随着围压增大而增大，这与其他学者[6,14–15,23]研究相符.

图9 不同土 Gmax–围压关系曲线Fig.9 Gmax–confining pressure curves of different soils

现有研究表明，最大动剪切模量和土的种类、相对密实度和平均有效围压有关，且试验频率对其影响不明显，结合本文试验数据，采用Hardin模型[14]，黄河泥沙的Gmax由下式表示：

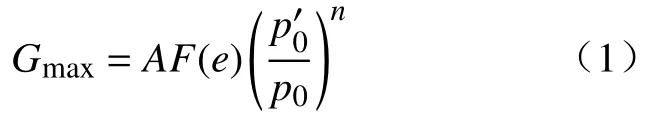
图10(b)为采用不同经验模型计算黄河泥沙的Gmax预测值与试验值的对比，其中梁珂等[7]基于南沙珊瑚砂提出了：

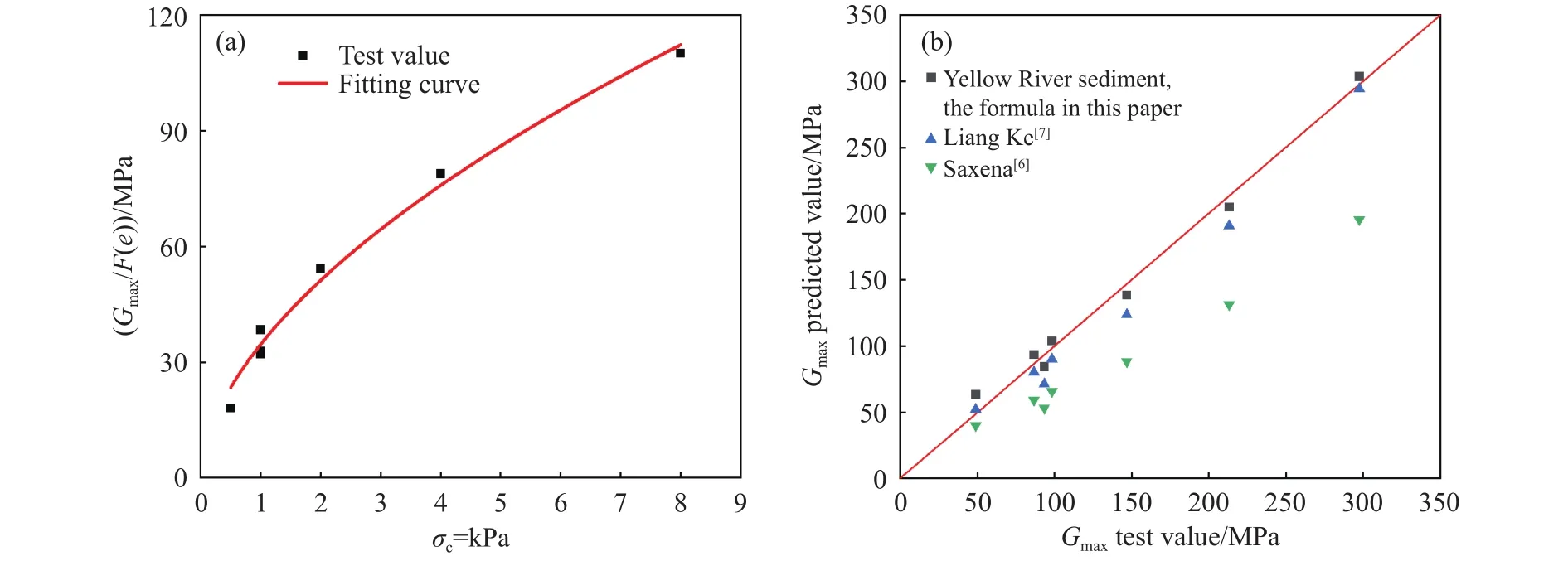
图10 (a) Gmax 归一化曲线图;(b)不同经验模型 Gmax 试验值与预测值对比Fig.10 (a) Normalized curve of Gmax; (b) comparison of experimental and predicted Gmax values of different empirical models

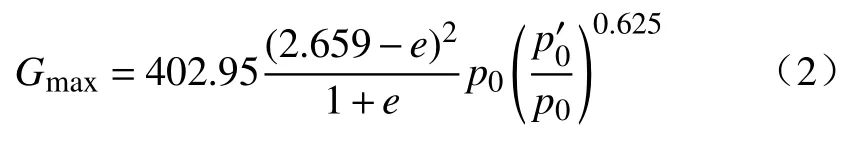
Saxena和Reddy[6]基于Monterey标准石英砂建立如下公式：

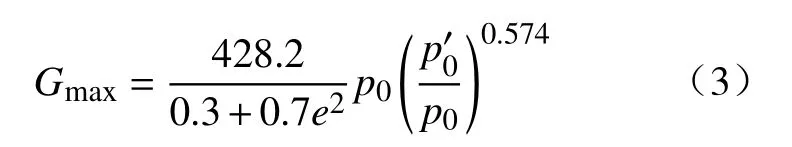
采用本文建议的模型预测的黄河泥沙G/Gmax预测值与试验值回归分析的决定系数R2=0.989，并用梁珂、Saxena所用模型进行对比分析，结果表明本文建议模型预测效果较好.各经验模型拟合所得Gmax值见表4.

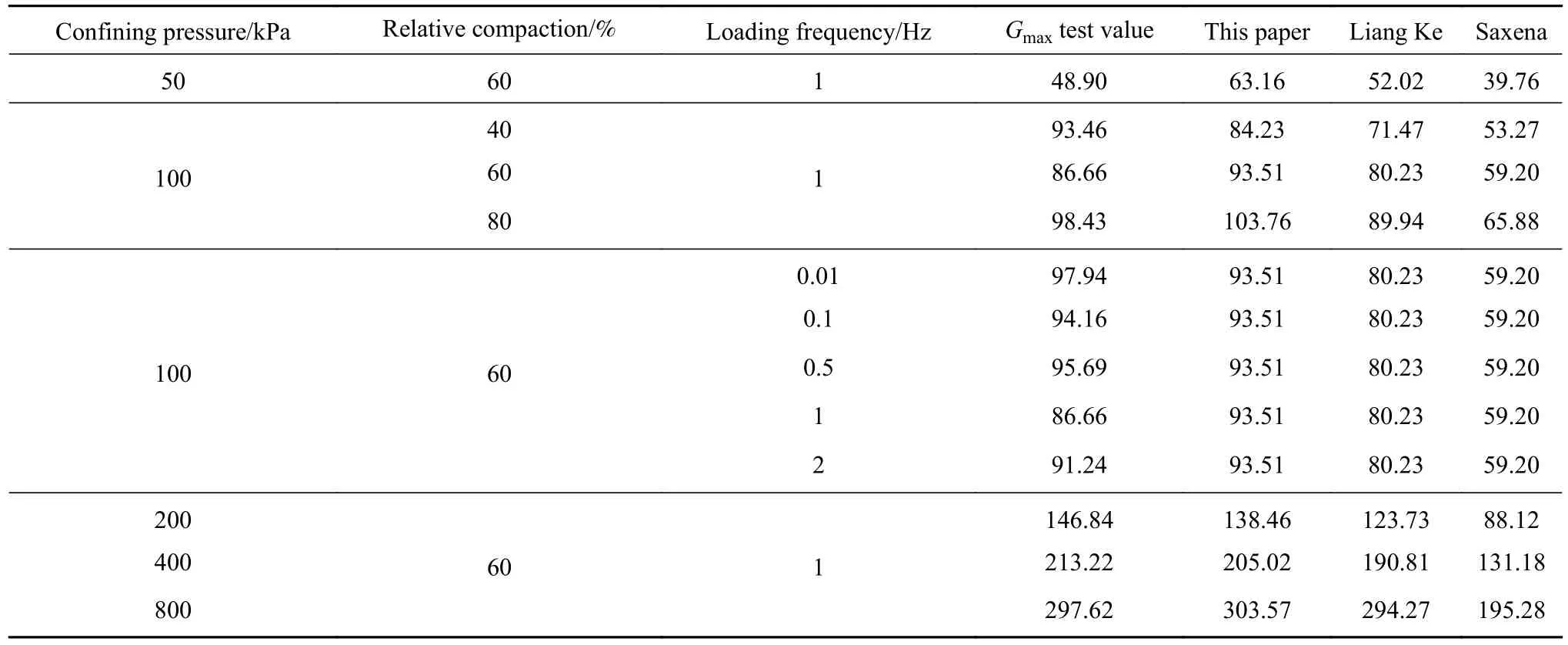
表4 Gmax 预测结果Table 4 Gmax prediction results

2.5 动剪切模量比

对不同工况下的动剪切模量用相应工况下的最大动剪切模量进行归一化处理，绘制G/Gmax与剪应变γd的关系曲线.图11为不同工况下动剪切模量比G/Gmax与剪应变γd的关系.

从图11可知，不同工况下，动剪切模量随剪应变的增大而减小，具有较好的非线性关系.当剪应变相同时，不同σc下黄河泥沙的G/Gmax–γd曲线呈现出明显差异，σc为 50、100、200 kPa时，G/Gmax与剪应变γd的关系曲线差异不明显；σc为 400 kPa、800 kPa时，G/Gmax值明显增大，即黄河泥沙的G/Gmax–γd曲线非线性减弱.随着剪应变的增大，不同围压下动剪切模量比的差值呈现先增大后减小的趋势，最终趋于重合.剪应变较小时，相对密实度为60%的G/Gmax小于相对密实度为40%的G/Gmax，剪应变较大时，G/Gmax随相对密实度的增大而增大.试验频率为 0.01～0.1 Hz时，G/Gmax差异不明显，当频率为 0.5、1、2 Hz时，G/Gmax随着频率的增大而增大，变化幅度不是特别显著.

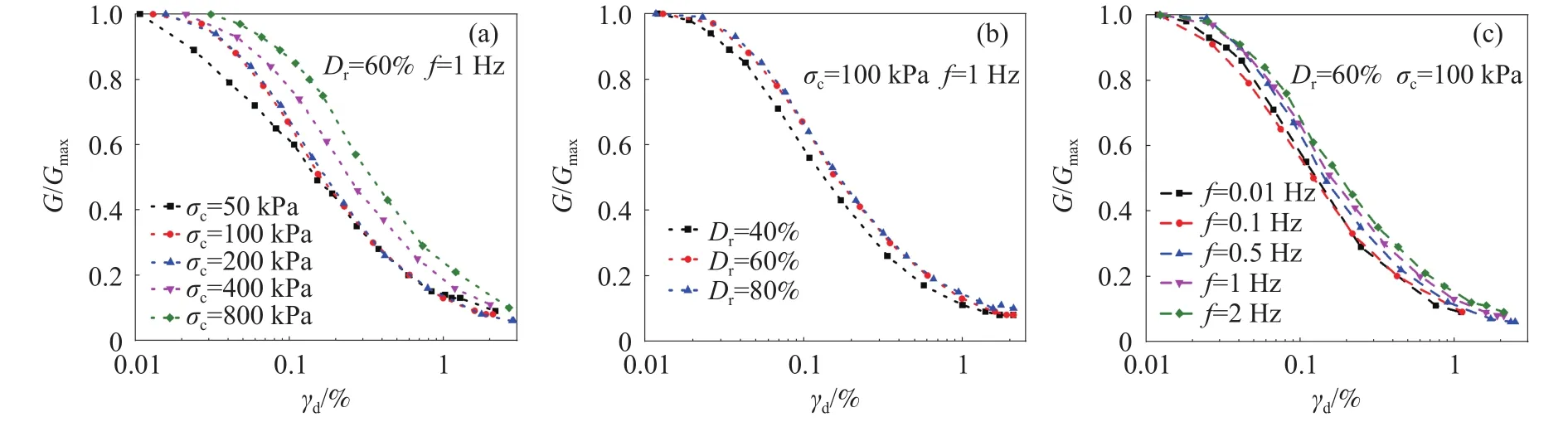
图11 动剪切模量比–剪应变关系曲线.（a）不同围压；（b）不同相对密实度；（c）不同频率Fig.11 Dynamic shear modulus ratio–shear strain curve: (a) different confining pressures; (b) different relative densities; (c) different frequencies

图12为不同围压下黄河泥沙G/Gmax与剪应变关系曲线[5,18–19,24]，并对比了围压相近时，不同沙砾土的动剪切模量折减曲线的上、下限.从图中可以看出，围压相近时，黄河泥沙的G/Gmax–γd曲线的上下限较粉土和黄土的宽，较Toyoura砂、砾石的折减曲线上下限窄；黄河泥沙的G/Gmax衰退速率较Toyoura砂、砾石的快，较粉土、黄土的衰退速率慢；黄河泥沙的折减曲线上限较Toyoura砂、砾石、黄土的上限高，较粉土的上限低.从图中曲线看，黄河泥沙动剪切模量折减曲线几乎包含了所有粉土动模量数据点，同时包含了部分的丰浦砂数据点，距离黄土和砾石曲线较远，这说明黄河泥沙动剪切模量折减曲线规律和其他土体材料相符，其动力特性接近于粉土和砂土，但与粉土和砂土并不完全一致，具有一定的特殊性.

2.6 动剪切模量比数学模型

采用Davidenkov模型[25]预测黄河泥沙动剪切模量比G/Gmax随剪应变幅值γd的变化关系：

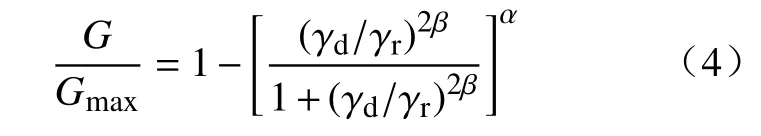
其中，α和 β均为拟合参数，参考剪应变γr取G/Gmax=0.5时的γd值，各试样的拟合结果见表5,拟合示意图如图13所示.各种工况下R2均大于0.95，可见该公式拟合效果较好.

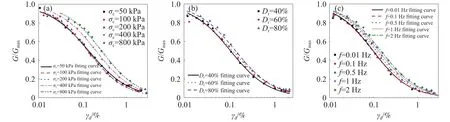
图13 G/Gmax–γd 拟合图.（a）不同围压；（b）不同相对密实度；（c）不同频率Fig.13 G/Gmax–γd fitting diagram: (a) different confining pressures; (b) different relative densities; (c) different frequencies

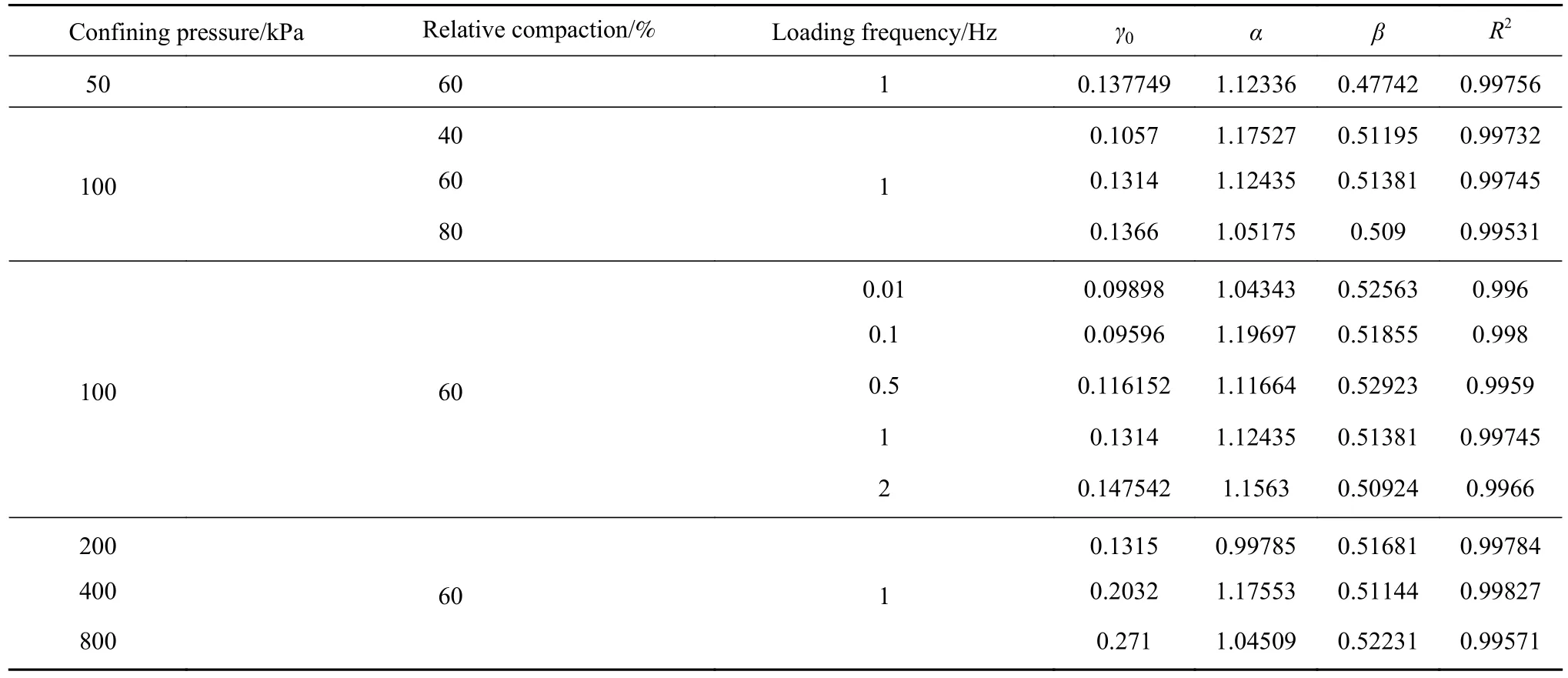
表5 G/Gmax–γd 拟合结果Table 5 G/Gmax–γd fitting results

2.7 阻尼比数学模型

根据动剪切模量比和阻尼比随剪应变的变化特点，借鉴刘鑫等[8]提出的经验公式对数据进行拟合:

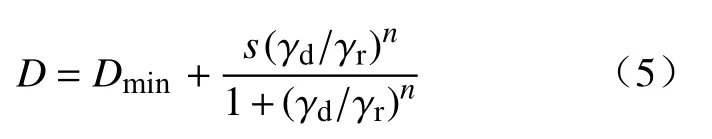
式中， γr为参考剪应变；Dmin为最小阻尼比；s，n为拟合参数，通过数学回归分析方法求解得到.

黄河泥沙的阻尼比与剪应变拟合曲线见图14，相关模型参数见表6.从图14可以看出，拟合曲线与试验值可以较好吻合.

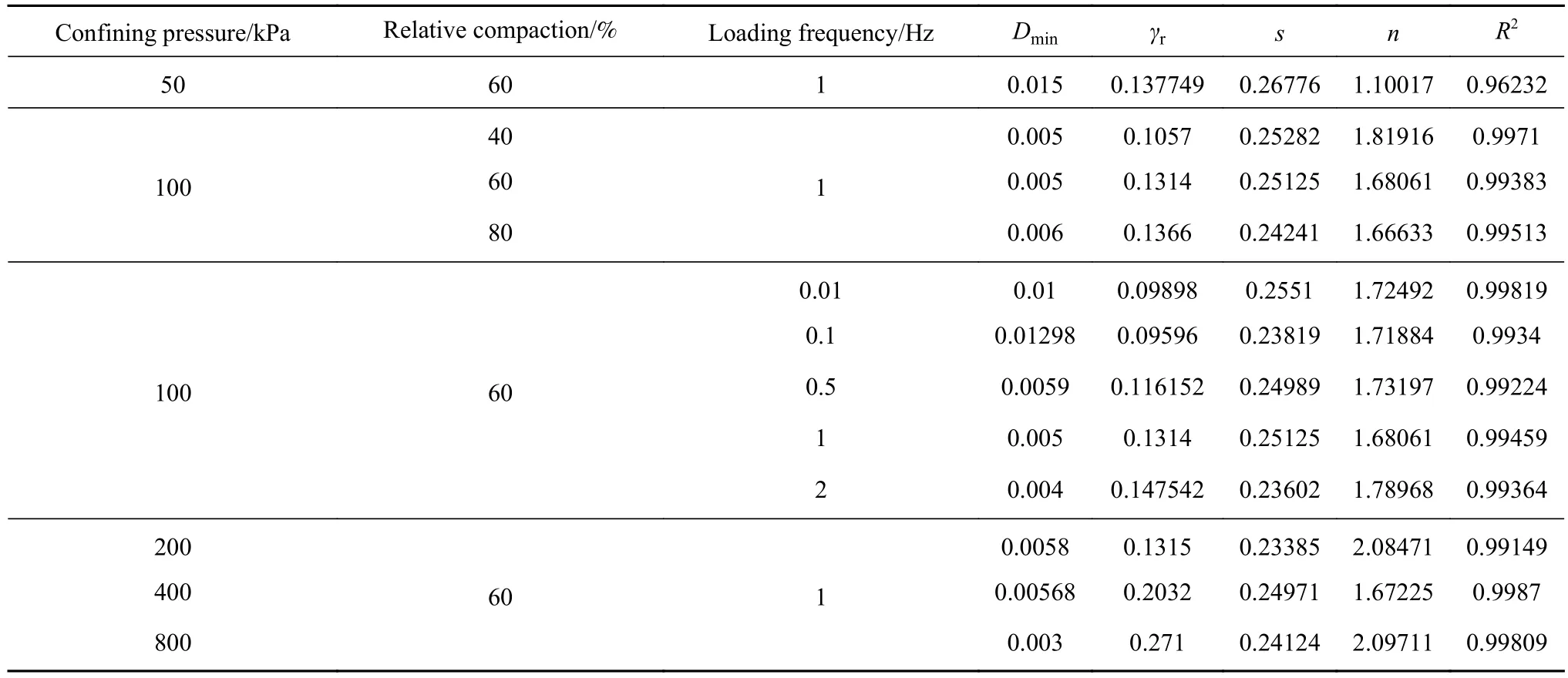
表6 D–γ拟合结果Table 6 D–γ fitting results

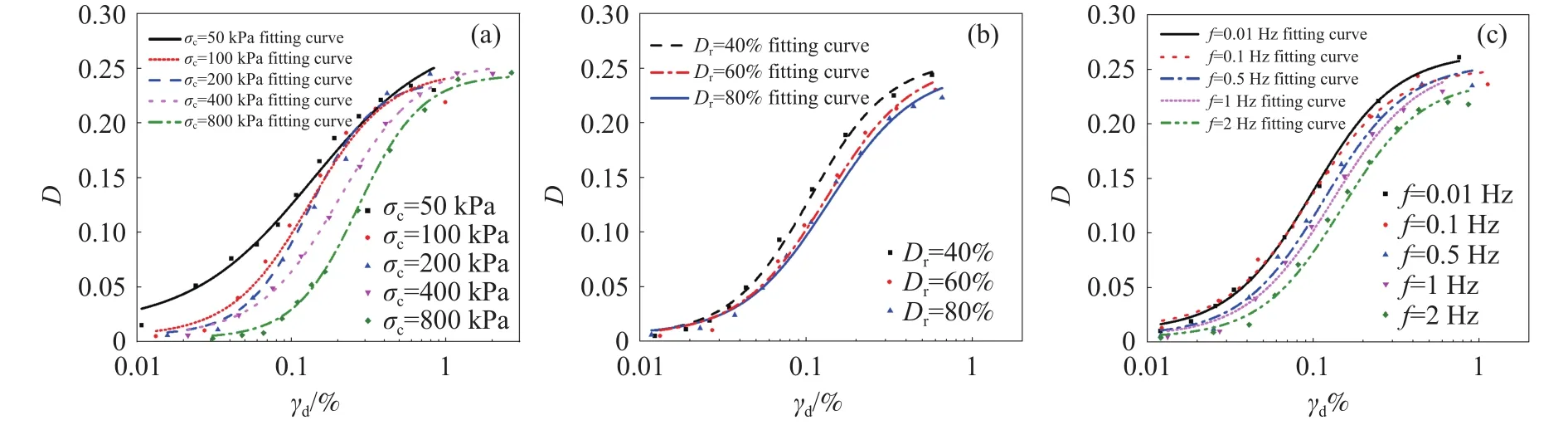
图14 阻尼比拟合曲线示意图.（a）不同围压；（b）不同相对密实度；（c）不同频率Fig.14 Damping ratio fitting curve diagram: (a) different confining pressures; (b) different relative densities; (c) different frequencies

3 结 论

本文通过在不同围压、相对密实度、试验频率条件下路用黄河泥沙的动三轴试验，对黄河泥沙的动力特性进行探究，试验结果表明：

（1）黄河泥沙的动剪切模量、阻尼比与剪应变关系可以用Hardin双曲线模型描述.其他条件相同时，随着剪应力的增大，不同围压下的剪应力–剪应变关系曲线的差别越来越明显.在一定的剪应力作用下，频率越低产生的剪应变越大.

（2）围压对黄河泥沙动剪切模量和阻尼比的影响最大，相同剪应变条件下，围压越大，动剪切模量越大.应变水平较大时，动剪切模量随相对密实度增大而增大；频率对动剪切模量影响不明显.阻尼比随围压的增大而减小；随相对密实度的增大而减小；不同频率对阻尼比的影响有不同影响，试验频率在0.01～0.1 Hz范围内，应变幅度较小时，阻尼比随试验频率增大而增大，但增大程度不明显；试验频率为0.1～2 Hz时，阻尼比随着试验频率的增大而减小.

（3）黄河泥沙的Gmax随围压的增大而增大，考虑围压和相对密实度对最大动剪切模量Gmax的影响，对比分析不同经验公式，给出了一种适合预测黄河泥沙的最大动剪切模量的经验公式.

（4）分析对比不同土的G/Gmax–γd和D–γd关系曲线，发现黄河泥沙动剪切模量折减曲线规律和阻尼比随应变变化规律和其他土体具有一定的相似之处，其动力特性更接近于粉土和砂土，并非完全一致.黄河泥沙在级配和动力特性方面具有自身的特点，具有一定的特殊性.

（5）采用Davidenkov模型能较好地描述黄河泥沙的动剪切模量比随剪应变的变化规律，结合试验数据，给出了一种适合分析黄河泥沙阻尼比的数学模型，并给出各种工况下相应的拟合参数.