基于树突神经网络的低轨卫星智能感知路由算法

刘 洋，王丽娜

1) 北京科技大学计算机与通信工程学院，北京 100083 2) 北京科技大学顺德研究生院，佛山 528300

在6G愿景下，地面通信网络与卫星通信网络相互补充，构建跨地域、跨空域、跨海域的空−天−海−地一体化网络，将实现真正意义上的全球无缝覆盖[1].低轨卫星通信相较中、高轨卫星通信，传输时延短、路径损耗小，多个卫星组成的星座可以实现真正的全球覆盖.因此，低轨卫星可在全球范围内提供快速且低延迟的互联网接入服务.星上路由技术是5G/6G新基建下卫星通信的关键技术之一，利用星间路由算法可以对卫星网络中数据的实时传输进行性能优化，保证数据的高效传输.路由算法与智能感知技术融合，可以提升路由的分析和决策能力.因此，本文将针对低轨卫星网络的智能感知路由算法进行研究.

由于卫星网路拓扑结构是动态变化的，根据应对拓扑结构动态变化的方法可将卫星路由算法分为两大类：静态虚拟拓扑的星间路由算法和动态星间路由算法.静态虚拟拓扑的星间路由算法基于系统周期划分思想，将卫星网络结构由动态转化为静态，再在静态结构下设计协议进行路由[2].文献[3]根据卫星的建链周期进行周期划分，进而在每个周期内进行时隙规划，研究了时分体制的指向性星间链路网络的路由算法，分别以跳数和时延作为约束条件进行路由选择.文献[4]将整个系统周期划分为固定长度的拓扑设计时间片，基于时延队列信息进行路由，提高了导航加权精度因子.文献[5]借鉴了虚拟拓扑的思想，在此基础上提出了一种能量感知的路由方案，根据卫星的不同能级采取不同措施保证数据传输，降低丢包率.上述这种将动态的卫星网络拓扑按一定的时间间隔划分为静态的网络拓扑序列进行分析处理的方法，由于事先建立路由表，卫星不需实时计算，协议开销较小.但该种方式未考虑路由表之间切换时的衔接问题[6]，并且由于路由表固定，难以应对卫星节点故障、拥塞，无法确保路由选择的服务质量 (Quality of service, QoS).

动态星间路由算法根据实时链路状态信息进行计算，能够更好应对卫星网络拓扑变化和网络流量变化[7].机器学习技术可以自动提取训练集中数据与标签之间的特征，对链路状态进行实时分析，在动态路由优化方面相对于传统的启发式方法显示出巨大的优势.文献[8]提出适用于低轨卫星的机器学习路由方法，将各卫星节点的负载状态输入置信域策略梯度优化神经网络，实现负载均衡，但该算法只考虑了一种QoS指标.文献[9]提出一种基于机器学习的卫星网络路由机制，路由的起始节点、目标节点、各QoS度量等参数作为神经网络的输入，输出一条路径.由于其只能从训练集固定标签中选取路径，若路径中某一节点出现故障，则会造成拥塞.文献[10]通过采用动态贪婪系数，对传统Q-Learning强化学习算法进行改进，改善了容易陷入局部收敛的问题，但是该算法对于目标节点奖励函数的设置并不明确.文献[11]提出了一种基于深度强化学习的软件定义路由优化方法，基于实时链路状态，通过不断地输出下一跳路由构成整个数据传输的路径[12].深度强化学习算法能够自适应动态变化的网络环境[13]，但当卫星网络规模较大时，很难直接输出满足复杂约束的路径[14]，会导致算法收敛时间较长.

近年来，一些研究基于流量或者星间链路质量进行实时感知，做出路由决策.文献[15]通过感知邻居节点的队列长度和能量进行路由决策，在降低卫星能耗的同时减轻网络的局部拥塞.但该研究仿真部分只用树莓派搭建了6个节点，未能很好地模拟实际星间链路情况.文献[16]根据卫星之间的链路状态信息确定水平和垂直传输的跳数和方向，对遇到故障节点的不同情况进行分析，但由于只以最短路径为目标，会导致数据集中在同一条路径传输，容易造成拥塞.将智能感知与路由相结合是未来重要研究方向，可以为路由选择提供保障.

针对静态卫星网络路由算法实时性差以及动态传统神经网络路由算法计算复杂度高等特点，为了实时感知星间链路的多种QoS因素，本文提出基于树突神经网络的低轨卫星（Low-Earth orbit，LEO）智能感知路由算法.该算法首先利用蚁群算法做出路由选择，收集输出结果，进而构造训练集，训练树突神经网络（Dendrite net，DD）.在星间链路态势感知阶段，对卫星之间的可视性约束进行分析，以此为前提得出当前时刻各个卫星之间的建链状态；设置链路监测周期，周期性获取星间链路的建链情况，实现星间链路态势感知；在神经网络链路质量感知阶段，将卫星节点之间的距离、时延、时延抖动、丢包率等链路状态信息作为树突网络的输入参数，训练好的树突神经网络通过对链路状态信息进行处理，输出满足多种QoS因素的下一跳路由选择的评估值矩阵；在路由决策阶段将评估值矩阵的倒数作为邻接矩阵通过迪杰斯特拉（Dijkstra）算法，得出源节点和目的节点之间的初始路径；最后周期性监测卫星网络拓扑，实时修正初始路径.

1 低轨卫星网络模型

本文研究的低轨卫星网络采用Walker星座，Walker星座由高度和倾角均相同的圆轨道卫星组成，星座中所有卫星呈均匀对称分布，同一个轨道面内卫星分布均匀，不同轨道面间卫星的相位持一定的相对关系[17].Walker星座卫星轨道可以由三个参数 (N,P,F)表示：N表示卫星总数、P表示轨道个数、F表示相位因子，则Walker星座中编号为i的卫星其升交点赤经W和升交点角距ui分别为：

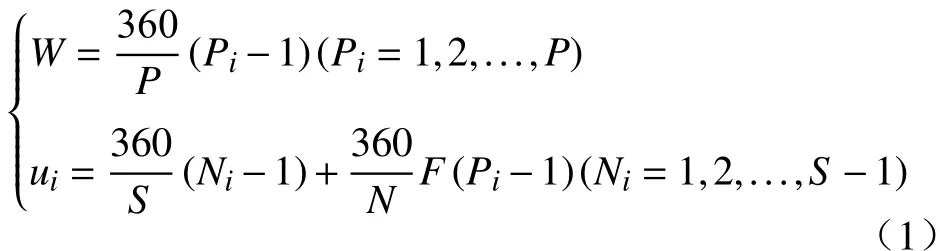
其中，S为每个轨道平面上的卫星数，Pi为卫星所在轨道平面的编号，Ni为卫星在轨道平面内的编号.本文所设置的低轨卫星网络基本星座构型为Walker（64/8/1），轨道高度为 800 km，轨道倾角为68.5°，星座轨道面的升交点赤经均分0～360°范围.通过 Satellite Tool Kit(STK)软件仿真，得到该构型的星座图以及其对应的星下点轨迹图分别如图1和图2所示.

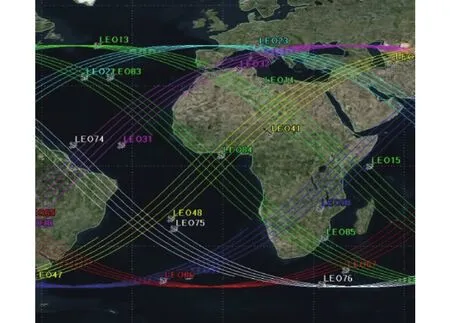
图2 星下点轨迹图Fig.2 Under-satellite point trajectory diagram

2 智能感知路由算法

星间链路状态变化频繁，无论是星间链路误码率过高导致的链路中断、星间相对运动导致的链路中断与重连或是卫星节点的失效，均将使网络拓扑处于非稳定的状态.因此，星间路由算法应具有动态感知卫星网络拓扑以及在变化拓扑下自适应重路由的能力[18].本文算法主要分为三个阶段：星间链路态势感知阶段、星间链路质量感知阶段、路由决策阶段.基于树突神经网路的低轨卫星智能感知路由算法流程图如图3所示.

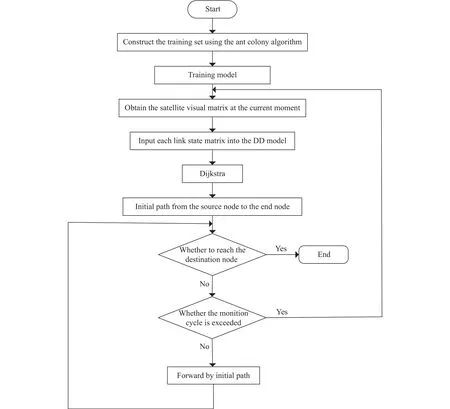
图3 算法流程图Fig.3 Algorithm flowchart

2.1 星间链路态势感知阶段

在星间链路的态势感知阶段，以卫星之间的可视性约束为前提并设置链路状态监测周期及时体察链路状态，使得星间路由能够对时变卫星网络的拓扑做出迅速调整.

2.1.1 星间链路建链条件

卫星之间可视是星间建链的基础，接下来将对星间链路建立的条件进行分析.卫星之间能否建链主要受以下两个方面的因素影响：

（1）卫星之间几何可视，即卫星之间的直线连线不受地球和大气层遮挡，是建立星间链路的前提条件；

假设地球半径为Re，考虑到对流层和电离层等外界因素对信号的影响，设大气层厚度为h，卫星Si的轨道高度为di， 卫星Sj的轨道高度为dj，星间链路距离为Lij.如图4为某时刻大气层与卫星Si和Sj的星 间链 路相 切的 情况 ， βij为 卫星Si相 对于Sj的俯仰角， βji为卫星Sj相对于Si的俯仰角.此时为卫星之间几何可视的边界条件，因此建立星间链路的几何可视约束为：

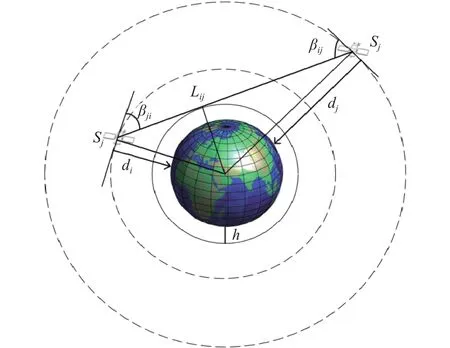
图4 某时刻卫星相对位置示意图Fig.4 Image of the relative position of the satellite at a certain moment

其中， θji为卫星Sj相对于Si的俯仰角，将式（2）转化为用距离Lij表示：

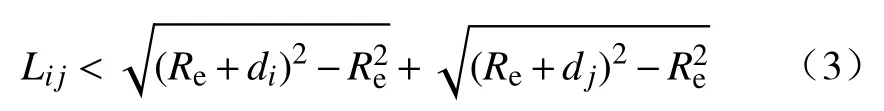
其中，Lij表 示卫星Si和Sj之间的距离.

（2）卫星之间天线可视，即两颗卫星均处于对方天线波束扫描范围内时才能完成信号的发送与接收，是建立星间链路的根本条件.设卫星Si和Sj的波束扫描范围分别为 γi、 γj，为满足天线可视约束， θji应满足如下条件：

将式（4）转化为用距离表示：

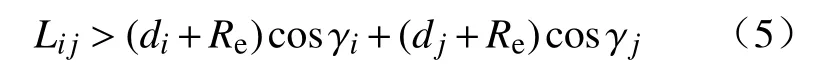
综合分析卫星之间的几何可视和天线可视，得出任意两颗卫星可以建立星间链路的充分必要条件为：

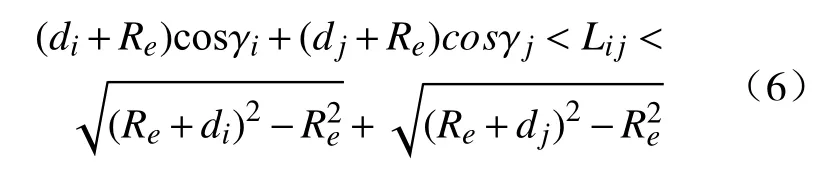
2.1.2 星间链路监测周期

若低轨卫星绕地运行周期为T，单轨道内有N颗卫星，则T/N即为LEO卫星网络的拓扑变化周期Ts.即最多经过Ts时间将有一颗卫星进入极地地区，进而卫星网络逻辑拓扑发生变化[19].本文以Ts为链路监测周期，超出链路监测周期时应重新计算卫星节点之间的建链状态，对路由进行修正，避免链路切换导致数据包的丢失.

2.2 星间链路质量感知阶段

在星间链路质量感知阶段需要对收集的卫星网络链路状态参数进行客观评估，以综合分析每条链路的质量、提高QoS.本文采用基于机器学习的评估方式，并以人工神经网络作为评估工具，计算各个节点之间的链路代价，输出下一跳节点选择的评估值矩阵.

2.2.1 路径代价及目标函数

端到端时延、时延抖动[20]、丢包率等均为影响卫星网络QoS的因素，卫星路由算法的设计应考虑多种QoS因素，避免网络拥塞.为提高QoS，本文提出的路由算法的路径代价综合考虑任意卫星节点i与j之间的距离、时延、时延抖动、丢包率，公式如下：

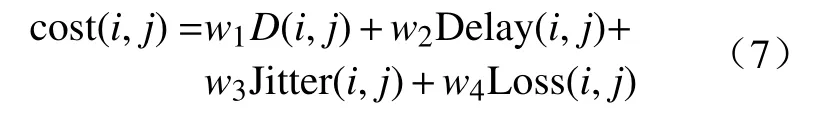
其中， c ost(i,j)为链路eij的路径代价，路径代价反映了卫星节点之间传输链路质量的综合评价[21].D(i,j)、Delay(i,j)、 J itter(i,j)、 L oss(i,j)分别代表卫星节点i与j之间的距离、信息传输时延、时延抖动和丢包率.wi表示各QoS因素所占的权重系数，系数之和为1，在本文中权重系数值将随着负载状态的变化而改变.当某一QoS指标变化较大时，其在路径代价函数中对应的权重系数将比其他指标的权重系数大，这样在路径选择时可以避免选择该指标较大的星间链路.

在卫星网络拓扑中， p ath(s,d)表示从源节点s到目的节点d所包含的路径，源节点到目标节点之间的最优路径即为路径代价最小的路径，目标函数及约束条件如下：

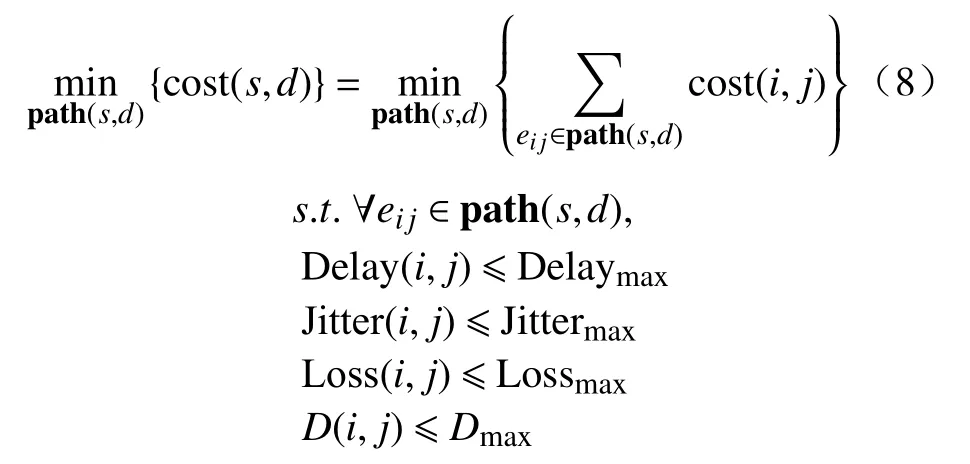
其中，eij∈path(s,d)表示源节点至目标节点路径中的边， D elaymax、 J ittermax、 L ossmax和Dmax分别为实时传输业务在LEO网络中所能承受的最大时延、时延抖动、丢包率，以及卫星之间满足可视性约束时的最大距离.为了保证计算时各QoS参数单位的统一性，需对其进行以下归一化处理[22]：

2.2.2 基于蚁群算法构造训练集

传统基于深度学习的路由算法在构造训练集时，通常以经典路由算法获取的一条完整路径作为训练集的标签.这样神经网络输出的结果只能从固定集合的路径中选取，若某一路径中的节点失效则易产生拥塞.因此，本文基于蚁群算法最终输出的概率转发矩阵作为训练集的标签，通过当前节点选择下一跳节点的概率值来评估对应的星间链路质量.

蚁群算法是一种启发式算法，蚂蚁为网络中进行路由信息收集与更新的数据包，将蚁群算法中的转发概率表对应为卫星网络的路由表[23]，链路QoS信息是蚂蚁选择下一跳节点的重要依据.神经网络模型的训练依赖于训练数集，本文通过改变不同负载状态下路径代价函数中的权重系数，得出更有效的训练集标签数据，以提高所训练的神经网络性能.构建训练集的具体过程如下：

首先，模拟不同负载情况下卫星节点之间的距离、时延、丢包率、时延抖动信息，并将这些状态信息通过蚁群算法得出卫星节点选择下一跳节点的概率矩阵.进而将所得到不同负载状态下的概率矩阵作为训练树突神经网络的标签，以此构建训练集，训练神经网络模型.当新的路由请求到达时，输入神经网络，输出当前状态下的评估值矩阵，将此结果作为新的标签加入训练集.这样通过半监督学习的方式优化标签，动态构造训练集，可以更好感知卫星网络状态信息，继续训练优化模型.

虽然通过蚁群算法可以直接得出任意两点间的路径，但每次通过蚁群算法计算源节点到目标节点的路径耗费时间过长，不利于星上实时决策.而本文算法通过改进路径代价函数中的权重，利用更有效的训练集，提前训练神经网络模型，提取出星间链路状态信息和星间链路质量评估值之间的逻辑关系.进行路由决策时，只需通过训练好的神经网络模型感知当前时刻的链路质量，基于感知信息做出路由选择.虽然前期训练神经网络的过程较复杂，但是在路由选择时可快速做出决策.

2.2.3 基于树突神经网络的星间链路质量评估

本文选用文献[24]中提出的树突网络(Dendrite net，DD)算法，DD算法的良好性能在文献[25]中得到验证.树突神经网络架构简单并且由于计算只包含矩阵乘法和哈达玛积，该算法的计算复杂度远比传统神经网络中的非线性函数计算复杂度低[26].在每一代前向传播中，树突神经网络都比传统人工神经网络速度快，有助于卫星网络实现低时延传输；路由算法所需的神经网络必须具有非常强大的输出层[27]，而DD算法可以有多个输出.综上，采用树突神经网络对卫星节点的状态参数进行客观评估，以确保卫星路由满足多种QoS目标优化是可行的.DD是白盒算法，可以将训练好的DD逻辑提取器转化为输入和输出关系谱[28].其中输入对应为卫星网络中各个节点的QoS信息，输出的评估值矩阵即为当前节点选择其余节点作为下一跳的概率.

DD模块表示如下：

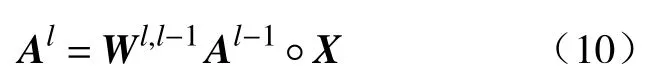
其中，Al−1和Al分别是模型的输入和输出，X代表树突神经网络的输入参数，Wl,l−1是从第l−1到第l个模型的权重矩阵，“◦”代表哈达玛乘积，图5为本文所需DD算法模型.

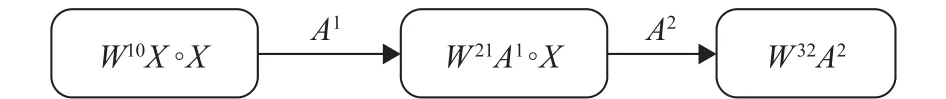
图5 DD 算法模型Fig.5 DD algorithm model

2.2.4 DD 学习规则

DD模块和线性模块的前向传播:

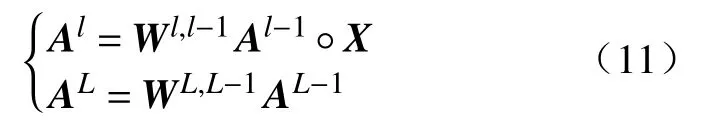
其中，L代表模型的最后一层，为线性模块.

DD模块和线性模块的误差反向传播规则:

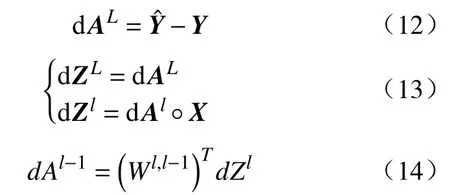
DD通过梯度下降进行权重调整：

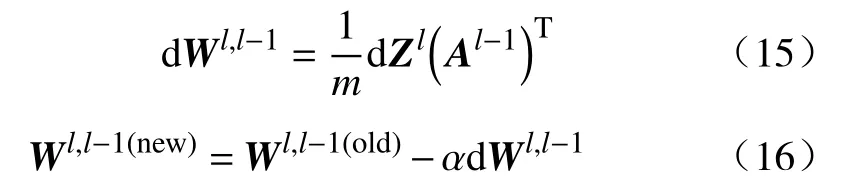
其中，m表示一个批次中训练样本的个数，α为学习速率.

将经过归一化处理后卫星之间的距离矩阵X0、时延矩阵X1、时延抖动矩阵X2、丢包率矩阵X3作为输入参数输入树突神经网络，树突神经网络内部算法表达式如下：

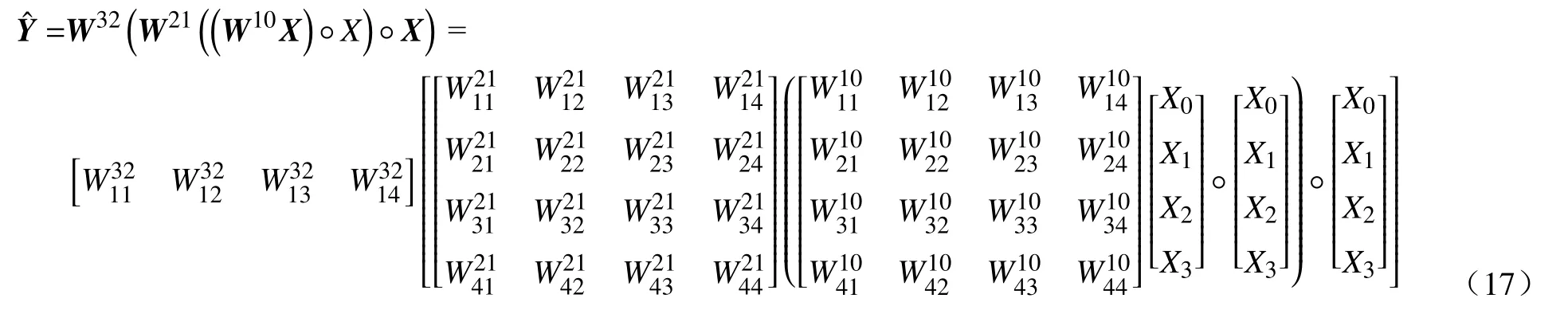
公式（17）是通过哈达玛乘积建立当前输入和先前输入的逻辑关系，式中W10是从第0到第1个模型的权重矩阵，W21是从第1到第2个模型的权重矩阵，W32是从第2到第3个模型的权重矩阵，其中初始化权重矩阵服从0～1均匀分布.树突神经网络每一层的权重W将利用训练集的标签Y，通过式(12)～(16)被不断训练调整，直至训练出误差较小、与目标函数拟合程度较高的树突神经网络.

树突神经网络经过与训练集的拟合，训练好的神经网络逻辑提取器将转化为关于链路状态参数输入和选择下一跳路由节点概率输出的关系谱.所输出的矩阵Yˆ是基于概率的路由，将其定义为评估值矩阵，其中卫星i与卫星j的链路所对应评估值为yi,j，则评估值矩阵表达式如下：

其中，输出的节点对应评估值越大，选择该节点作为下一跳的概率越大；当两节点间不满足可视性约束时，对应评估值为0；当最佳路径中某一节点出现故障时，可选择评估值相对较高的其他卫星节点，避免链路拥塞.该评估值矩阵综合考虑多种QoS因素，并且不像启发式算法过于依赖人类经验，而是通过人工神经网络不断优化训练得到的客观评估结果.

2.3 路由决策阶段

Dijkstra算法是常见的最短路径算法，在路由决策阶段将评估值矩阵取倒数作为Dijkstra算法的输入邻接矩阵，可输出一条满足目标函数、链路代价最小、具有QoS保障的最佳初始路径.一方面，在监测周期内按初始路径进行路由，若超出监测周期则需重新计算初始路径中当前节点与其对应下一跳节点之间的建链状态；若不可建链，需获取当前时刻的节点状态信息并输入树突神经网络，重新进行路由选择，对初始路径进行修正，实现卫星路由的实时感知.另一方面，当初始路径中某一节点的下一跳节点出现故障时，可选择当前节点的次佳下一跳节点，再通过Dijkstra算法得出路径.

3 算法性能评估

3.1 仿真环境配置

本文首先利用 Satellite Tool Kit软件创建一个新的场景，场景时间设为 2 Dec 2020 04∶00∶00.000至 2 Dec 2020 05∶00∶00.000.先生成 seed 卫星，再通过Walker方法快速创建Walker星座，Walker的参数设置如表1所示.

表1 Walker参数设置Table 1 Parameter setting of the Walker constellation

取其中24颗低轨卫星，利用STK对卫星之间的可视性约束进行分析，可得出卫星之间在任意时刻的建链情况，导出卫星之间的可视性矩阵.低轨卫星绕地运行周期约为85 min，单轨道内有8颗卫星，因此监测周期为 10 min.每隔 10 min 对所得路径涉及卫星节点之间的可视情况进行确定，避免整个卫星网络拓扑状态发生变化时，有链路断开未能及时发现.

之后，通过MATLAB和STK的互联接口将report中链路可视矩阵信息以及卫星之间的距离矩阵传给MATLAB；利用MATLAB对卫星之间的信道进行建模，同时生成卫星之间的多普勒频移，进而模拟卫星之间的带宽、时延、时延抖动、丢包率矩阵.链路参数设置如表2所示.

表2 链路参数设置Table 2 Parameter setting of the link

在初始时刻，路径代价函数中各权重系数值均为0.25.当前网络中数据包传输完成后，统计平均端到端时延、丢包率、时延抖动，分别计算当前负载状态与前一负载状态相比三种QoS指标增加的百分比.假设平均端到端时延、丢包率、时延抖动分别增加了a、b、c,则下一负载状态下路径代价函数中权重系数分别为：

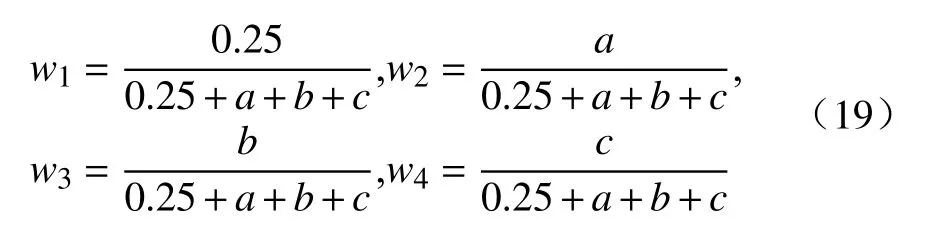
3.2 仿真结果分析

图6为通过MATLAB软件仿真得到的树突神经网络拟合图，由此可以发现当训练 3 ×105代之后误差曲线趋于稳定，并且误差很小，可以以高概率收敛到全局最优，表明本文所选用的树突神经网络拟合性能较好.图7为输入第1个卫星节点至其他23个卫星节点的状态信息时，模型输出当前卫星节点选择其他卫星节点的概率.以该概率作为评估值，评估值越大，选择对应节点作为下一跳的可能性越大；当评估值为0时，表明两个卫星节点之间不满足可视性约束，不能建立星间链路.

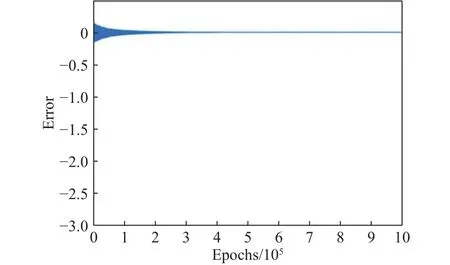
图6 树突神经网络拟合图Fig.6 Dendritic network fitting graph

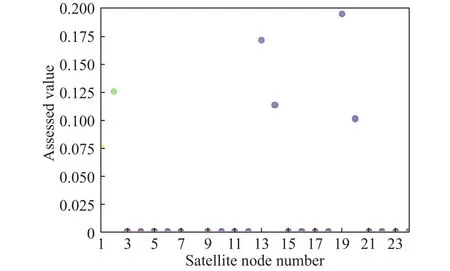
图7 选择下一跳卫星节点的概率Fig.7 Probability of selecting the next hop satellite node

为了验证树突神经网络路由算法的性能，分别与蚁群算法（Ant colony algorithm, ACA）和 Dijkstra算法进行仿真对比.在网络负载量较低时，三种算法仿真得出源节点1至目的节点3的路径分别为蚁群：1—20—3，Dijkstra：1—2—3，树突神经网络算法：1—2—3；节点12至节点15的路径分别为蚁群：12—23—14—8—15，Dijkstra：12—13—8—15，树突神经网络算法：12—13—8—15；随着网络负载量增加，源节点1至目的节点3的路径分别为蚁群：1—2—19—3，Dijkstra：1—2—3，树突神经网络算法：1—19—3；图8为给定相同源节点和目的节点的条件下，三种算法的平均跳数和最大跳数对比图.由于蚁群算法属于启发式算法，其容易陷入局部最优解、收敛性较差，有时需较多跳数才可到达；Dijkstra算法在进行路由选择时直接考虑最短距离路径，并不考虑所选链路的拥塞情况，因此其只需较少的跳数即可达到目的节点；本文算法在综合考虑多种QoS因素的情况下，可以避开拥塞节点.在实际工程中，卫星路由的跳数应尽可能小.本文所提路由算法的平均跳数与Dijkstra算法一致，这表明其在避开拥塞节点时并未以牺牲路由跳数为代价.接下来将对三种路由算法在时延、丢包率、时延抖动方面的性能进行比较.

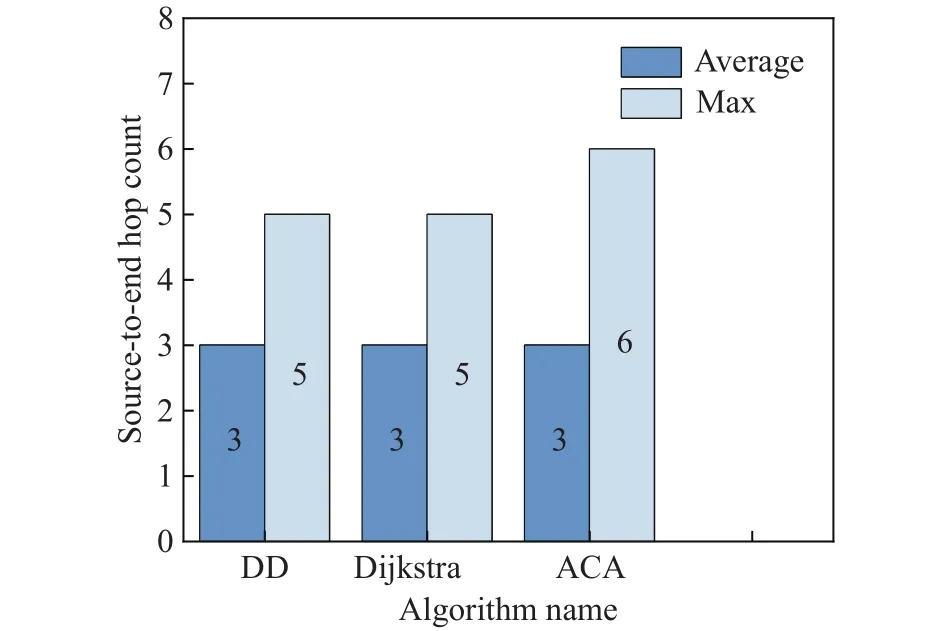
图8 相同源节点至目节点的路由跳数对比Fig.8 Comparison of route hops

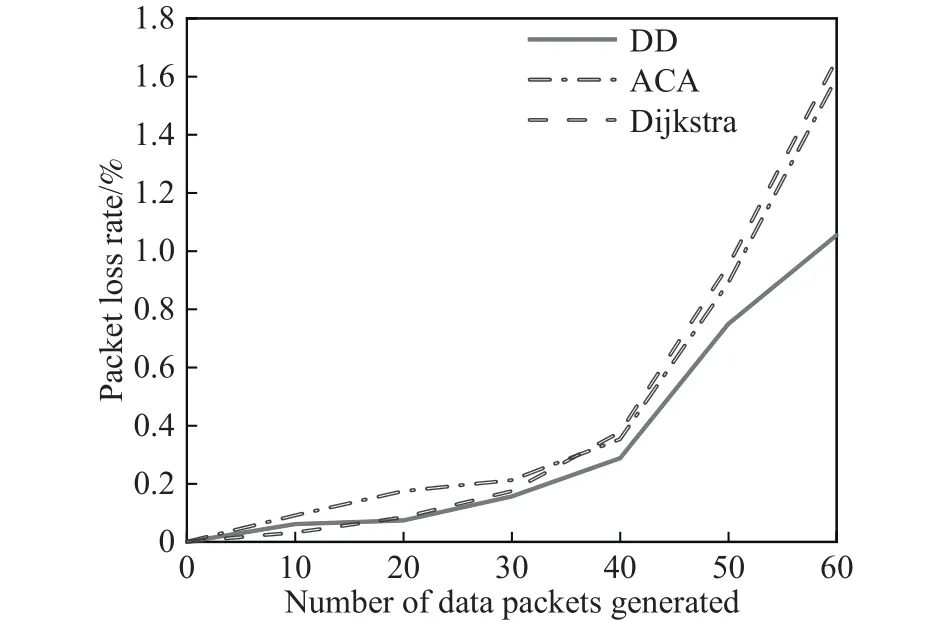
图10 端到端平均丢包率对比Fig.10 End-to-end average packet loss rate comparison

由图9至图11所示，随着数据包产生个数的加大，由于网络负载量不断增加，三种算法的端到端时延、丢包率以及时延抖动均成上升趋势.在数据包产生个数小于20时，由于卫星网路负载量较低，三种路由算法的时延、丢包率、时延抖动均较低.随着数据包产生个数的增多，本文算法的性能优势逐渐明显，其时延、丢包率、时延抖动均比Dijkstra算法以及蚁群算法低.这是因为Dijkstra算法直接选取最短距离路径进行路由，并不考虑链路质量，随着时间推移，最短路径上极易出现拥塞，导致时延、丢包率、时延抖动大幅度增加，而其他路径带宽利用率低、浪费资源；蚁群算法虽考虑多种QoS因素，性能与Dijkstra算法相比较好，但其收敛性较差.本文所提算法性能的提升主要有以下原因：其一，本文算法通过改变路径代价函数在不同负载状态下的权重系数来训练树突神经网络，可以避免选择QoS指标不好的链路；比如当网络中平均时延增长较多时，由于时延权重与其他指标的权重相比较大，接下来进行路由选择时，在综合考虑多种QoS指标的情况下会避免选择时延较大的路径；其二，通过半监督学习的方式动态构造训练集可以优化树突神经网络模型，利用树突神经网络自动调整全局卫星网络链路的评估值，更好地感知网络的状态信息，辅助做出智能路由决策.最终，当某一节点数据量较多时，可通过感知的链路权重信息自适应调节，避免选择易拥塞节点，从而降低整个卫星网络的平均时延、丢包率和时延抖动.

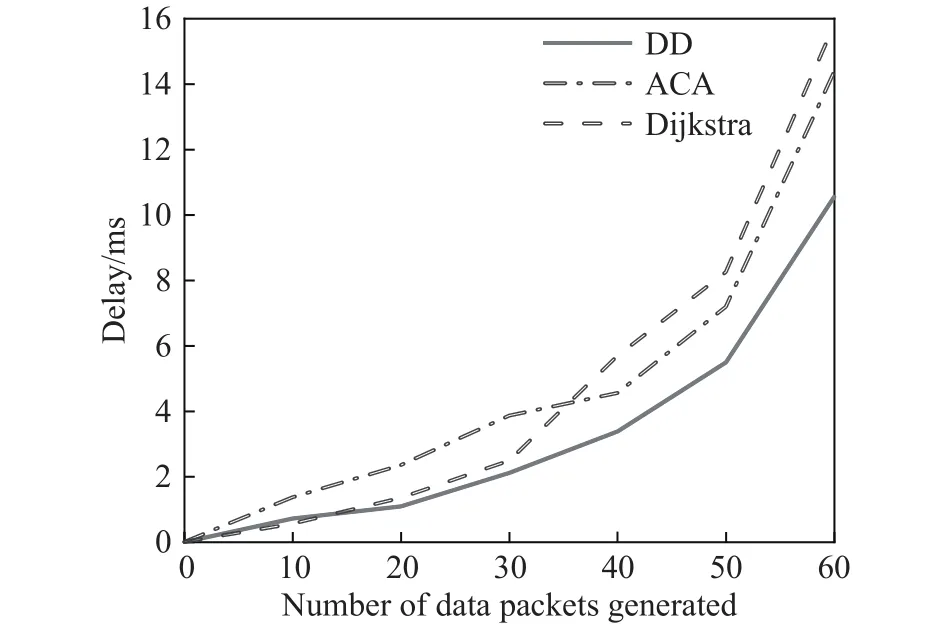
图9 端到端平均时延对比Fig.9 End-to-end average delay comparison

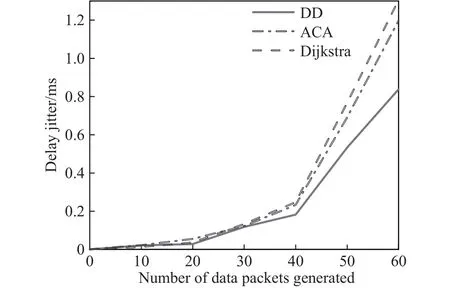
图11 端到端平均时延抖动对比Fig.11 End-to-end average delay jitter comparison

4 结论

本文提出一种基于树突神经网络的低轨卫星智能感知路由算法，星间链路态势感知阶段，周期性分析星间可视性情况；采用树突神经网络对链路状态参数进行分析处理，感知链路的综合服务质量，输出下一跳路由选择的评估值矩阵；在路由决策阶段将评估值矩阵倒数作为邻接矩阵通过最短路径算法，进而得出源节点和目的节点之间的初始路由路径；最后通过周期性监测修正初始路径以应对卫星节点失效.仿真结果表明：在相同数据包到达的情况下，该路由算法和传统路由算法相比性能更加优越.