海上风电桩–筒复合基础承载性能研究

孙艳国，许成顺，杜修力，王丕光，席仁强，孙毅龙

北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124

生态环境事关人类生存和可持续发展，需要世界各国共同应对挑战[1].随着能源短缺以及环境污染等问题的加剧，世界各国都在加快探索和发展新型可再生能源技术.碳中和不仅是人类应对全球气候变化的共识，也是世界各国的共同目标.到2060年我国将实现 “碳中和”的宏伟目标，这促进了我国新能源技术的发展[2].海上风电相对其他新能源具有安全、有效发电时间长以及不占用陆地资源等优势，在世界多个国家得到快速发展[3].我国海岸线较长，具有丰富的海上风能资源，大量的海上风电场已经建成或正在建设中[4].

目前，已建成的海上风电场主要位于近海，且装机风力发电机功率较小.但随着海上风电场逐渐向深远海和大兆瓦风力发电机发展[5–6]，对海上风电基础的承载性能提出了更高的要求，同时场地条件对于海上风电基础承载性能有较大的影响[7–8].为应对这些变化，众多学者对多种适用于海上风电的新型基础进行了开拓性的研究.Faizi等[9]基于复合三筒基础的研究指出，在原有基础上增加圆形平板可有效提高基础的抗倾覆能力，进而提升结构的整体承载性能.Yang等[10]和Li等[11]通过模型试验以及数值模拟对新型伞形基础在正常场地以及冲刷场地情况下动力响应进行了研究，其研究成果表明在单桩周围增加伞状附属结构能提高基础稳定性.Wang等[12]提出在单桩基础周围增加平台结构，其离心机模型试验的研究表明平台结构的增加可极大提升基础的承载性能，为复合基础的研究提供参考依据.朱东剑[13]结合单桩基础与筒型基础，构造出一种新型复合基础，并对新型复合基础承载性能的影响因素进行研究.刘润等[14–15]对单桩复合筒基础的共同承载机制与复合基础承载的包络线进行了研究，其结果表明复合基础中桩主要承担竖向荷载和大部分弯矩，而筒结构主要承担水平荷载和部分弯矩，并指出复合基础有效地提高了基础结构的承载性能.Wang等[16]对单桩基础、单筒基础以及桩–筒复合基础进行对比研究，研究结果表明相比于砂土，在软黏土中的基础上增加筒结构对结构整体承载能力的提升效果更好.Chen等[17]在桩–筒复合基础静荷载和动荷载的响应研究中指出，复合基础能够减小桩的入土深度，且附加的筒结构可以减小环境荷载作用下基础的转角和水平位移.刘红军等[18]对桩–筒复合基础结构进行了优化，推动了桩筒复合基础在实际工程中的应用.Li等[19]在筒基础上部进行抛石构造桩–筒复合基础，在筒结构上部所增加的竖向荷载使得筒与土之间的摩擦力以及主动土压力的增加，从而提高了基础的承载能力，同时其研究成果证明这种复合基础在松软场地中提升效果更加明显，这与Wang等[16]的研究成果相同.综上所述，将单桩和筒结构结合来构造桩–筒复合基础可以有效的提高基础的承载性能，尤其适合应用于以软弱场地条件为主的海上风电工程.

现有研究主要针对匀质黏土或砂土，而关于筒结构尺寸与土体非匀质特性系数对桩–筒复合基础承载性能的影响还缺少系统研究.本文基于有限元软件ABAQUS平台，建立了一系列桩–筒复合基础三维有限元模型，研究了饱和黏土场地中不同的筒结构尺寸和饱和黏土非匀质特性系数时，竖向荷载V、水平荷载H以及弯矩荷载M作用下基础承载特性，并通过正交试验法对承载力系数的影响因素进行分析，所得到的研究成果可为桩–筒复合基础在海上风电场中的广泛应用提供参考.

1 有限元模型

1.1 计算模型

通过钢管桩与钢筒组合的形式构建桩–筒复合基础，筒结构与钢管桩之间可以通过注浆的方式连接[13].本文建立有限元模型研究筒结构尺寸以及饱和黏土非匀质特性系数对桩–筒复合基础承载性能的影响.桩与附加筒结构之间采用绑定接触.钢管桩尺寸固定，桩入土深度l= 30 m，壁厚t= 0.05 m，外部直径d= 5 m.筒入土深度L= 2、6、10 m，筒直径D= 10、15、20 m，壁厚为T= 0.05 m.桩和筒结构采用钢材，模型中采用线弹性本构模型，钢材密度γs= 7800 kg·m–3，弹性模量Es=1013kPa（相对土体弹性模量足够大，视为刚体），泊松比λs= 0.3，采用六面体八节点线性减缩积分单元（C3D8R）模拟.复合基础中筒结构、桩与土体之间绑定，限制基础结构与地基土体之间的相对位移.

现有研究结果表明基于Tresca屈服准则的理想弹塑性本构模型能够有效地模拟饱和黏土的力学行为，众多学者基于Tresca屈服准则开展了大量的饱和黏土场地中基础承载性能研究[20–24].为验证本文有限元模型的可靠性，对文献[20]中相同尺寸的筒型基础进行水平和竖向的各单向极限承载力研究，计算结果如图1所示，图1中Ab为文献[20]中筒基础上部的表面积，Hult为水平极限承载力，Vult为竖向极限承载力.由图1可看出，本文的数值计算结果与Mehravar等[20]的计算结果吻合较好，说明本文模型具有一定的可靠性.

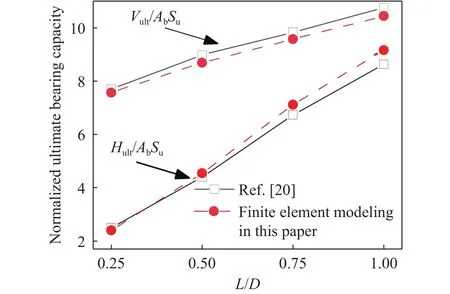
图1 有限元模型验证Fig.1 Validation of the model

本文研究的地基土体中采用非匀质饱和黏土，土体单元类型采用六面体八节点杂交单元（C3D8RH）.土体有效重度为γ'= 6 kN·m–3，泊松比λd= 0.49，土体弹性模量Ed= 400Su，Su为饱和黏土的不排水抗剪强度，Su随着深度变化如下式：

式中，Sum为泥面处的不排水抗剪强度，z为泥面下某点的深度，k为不排水抗剪强度随着深度变化率，如图2所示.

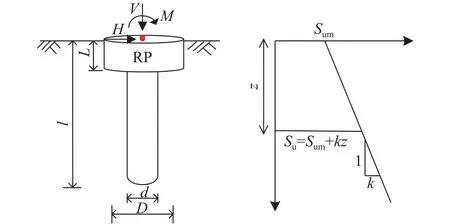
图2 桩–筒复合基础形状、荷载加载条件及土体条件Fig.2 Pile–bucket composite foundation geometry, load conventions,and saturated clay conditions

现有研究成果表明非匀质饱和黏土场地中，基础的承载性能不仅仅取决于某一个单因素Sum或k[21,23–24]，而是与量纲一参数kD/Sum有关.因此，饱和黏土场地的非匀质特性采用参数K=kD/Sum表达，取D= 10 m，具体参数如表1所示.Su随着k在 1.2～1.3 kPa·m–1内变化，通过改变泥面处的不排水抗剪强度Sum值即可得到不同的饱和黏土的非匀质特性系数K.

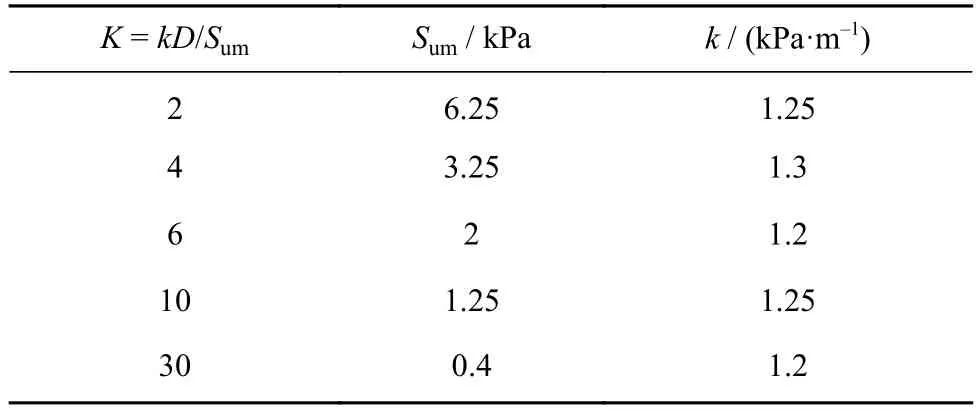
表1 饱和黏土非匀质特性Table 1 Inhomogeneous characteristics of saturated clay

为兼顾计算效率及计算精度，桩–筒复合基础周围土体网格尺寸较小，并对网格数量进行敏感性分析，最终确立网格划分方法，如图3所示为筒直径为20 m，筒入土深度为2 m时桩–筒复合基础以及周围土体的有限元网格.为减小模型边界效应对有限元计算结果的影响，通过多次试算得到合理的土体边界取值范围，最终确定土体高度为60 m,直径为100 m.对计算案例进行编号，采用‘D+筒的直径+L+筒的入土深度+非匀质特性系数+荷载作用方向’表示，例如D15L6K4-V表示饱和黏土非匀质特性系数为4，桩–筒复合基础中筒直径为15 m且入土深度为6 m时竖向荷载作用下基础承载特性.

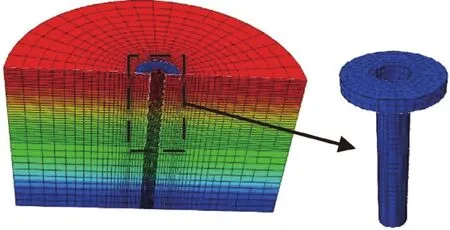
图3 有限元计算模型Fig.3 Finite element model

1.2 极限承载力的确定

如图2所示，在泥面处基础的中心点建立参考点RP作为荷载加载点，竖向荷载V、水平荷载H以及弯矩荷载M通过位移控制法进行施加.各向荷载作用下桩–筒复合基础的极限承载力通过位移–荷载曲线中两条切线的交点获得[25]，如图4为D15L10K4-H水平极限承载力Hult确定的方法，将切线交点处所对应的水平荷载视为基础的水平极限承载力，所得基础各单向极限承载力通过几何尺寸以及饱和黏土抗剪切强度进行量纲为1处理得到承载力系数，如表2所示，表中A= πD2/4，D为筒结构直径；Su0为某一深度处黏土不排水抗剪强度，根据Butterfield等[26]与Byrne和Cassidy[27]所建议的评判标准，Su0取复合基础中间深度处黏土不排水抗剪强度.

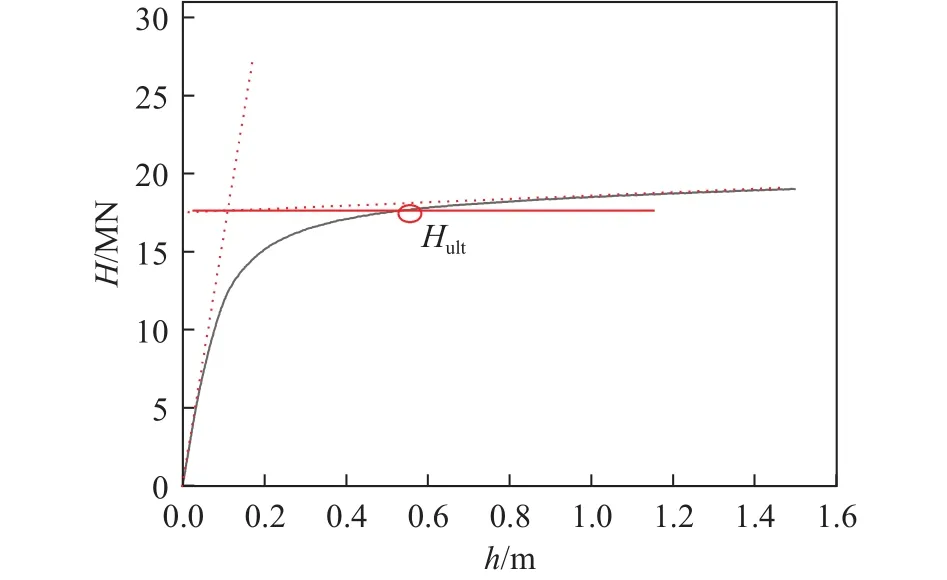
图4 极限承载力确定Fig.4 Determination of the ultimate bearing capacity

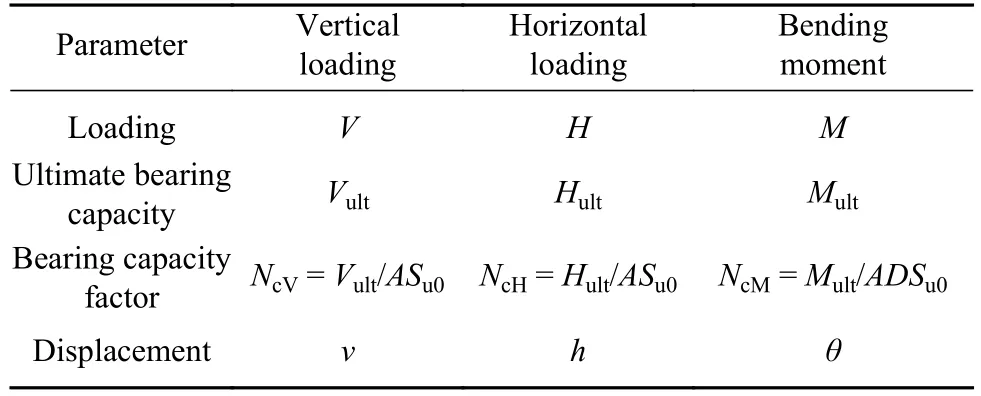
表2 荷载及位移符号规定Table 2 Sign conventions for loads and displacements

2 桩–筒复合基础水平承载特性

2.1 系数 K对水平极限承载力的影响

通过有限元计算，得到不同筒结构尺寸以及不同饱和黏土非匀质特性系数时桩–筒复合基础的水平极限承载力.为进行归一化研究，将水平极限承载力转化为水平承载力系数NcH，NcH=Hult/ASu0.图5(a)、(b)、(c)分别为筒直径D= 10、15、20 m时，桩–筒复合基础水平承载力系数NcH与饱和黏土的非匀质特性系数K之间的关系.从图中可以看出水平承载力系数NcH随着K的增加逐渐减小，且两者关系可以用指数函数来描述.这是由于随着K的增加，桩–筒复合基础深度内土体不排水抗剪强度均值减小.

图5 桩–筒复合基础水平承载系数NcH与K之间的关系.(a) D = 10 m; (b) D = 15 m; (c) D = 20 mFig.5 Horizontal bearing capacity factors of the pile–bucket composite foundations (NcH) with K: (a) D=10 m; (b) D=15 m; (c) D=20 m

2.2 筒直径D和入土深度L对水平承载特性的影响

图6(a)和(b)分别为桩–筒复合基础水平承载力系数NcH与筒直径D、筒入土深度L之间的关系.如图6(a)所示，NcH与D之间呈曲线关系，且随着D增加逐渐减小，非线性拟合结果见式(2)；如图6(b)所示，NcH随L的增加而线性增加，其线性回归结果见式(3).为保证拟合公式量纲统一，取单位长度O= 1 m.从式(2)和式(3)中可以看出，D和L对复合基础水平承载特性影响的交互作用明显.图7为NcH与D、L之间的三维关系图，从图中可以看出D和L对NcH的影响存在明显的交互作用.

图6 桩–筒复合基础水平承载系数NcH与D(a)和L(b)的关系Fig.6 Horizontal bearing capacity factors of the pile–bucket composite foundations (NcH) with D(a) and L(b)

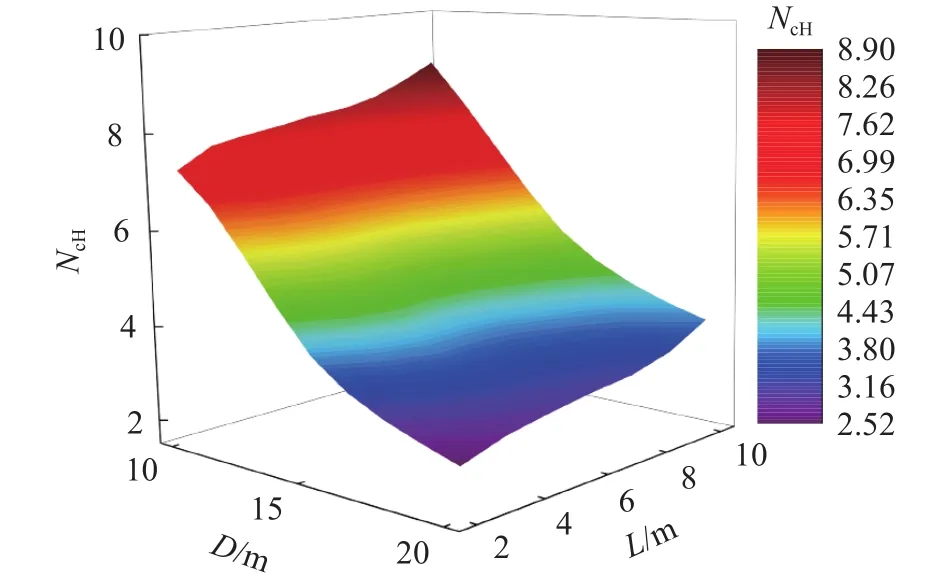
图7 D和L对水平承载特性的影响Fig.7 Effect of D and L on the horizontal bearing capacity factors

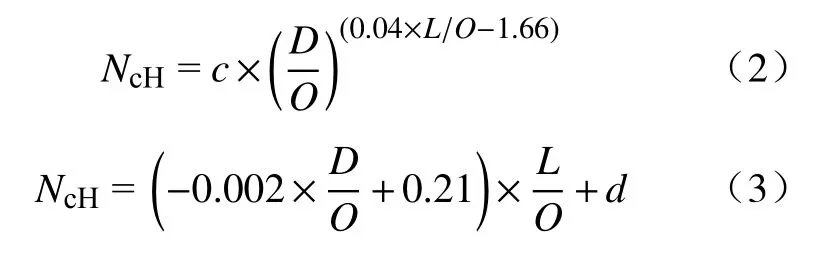
式(2)为NcH与D的关系，式中c为与L和K相关的值，它在302.7～146.3之间变化，且随着K的增加而减小；式(3)为NcH与筒入土深度L的关系，式中d为与D和K相关的值，它在–0.72～0之间变化，且随着K的增加而减小.

3 桩–筒复合基础竖向承载特性

3.1 系数 K对竖向承载力系数的影响

桩–筒复合基础的竖向承载力特性通过竖向承载力系数值NcV描述，NcV=Vult/ASu0.图8(a)、(b)、(c)分别为筒直径D= 10、15、20 m 时，NcV与K之间的关系.从图中可以看出K对NcV影响较小，随着K的增加NcV大小变化较小.筒入土深度较小时，NcV与K呈较缓变化的指数关系，且随着K的增加NcV逐渐减小；当K的增加到一定值时，NcV大小趋于稳定.当筒入土深度L较大时，NcV不随着K变化而变化，NcV大小基本保持不变，如D20L10-V中，K= 2时，NcV= 8.94；K= 30时，NcV=8.93，两者大小几乎相等.

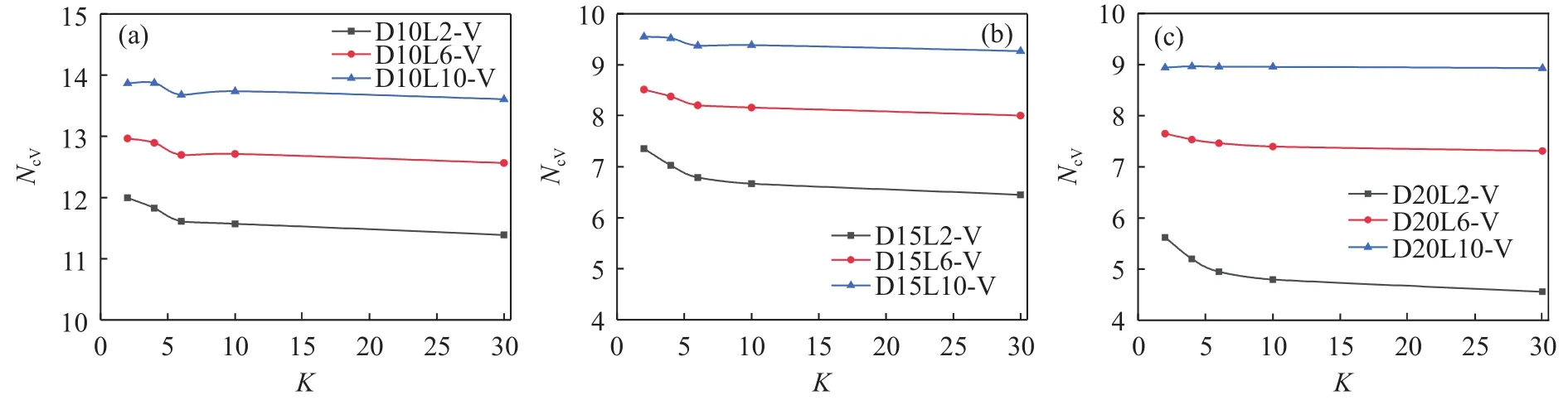
图8 桩–筒复合基础竖向承载系数NcV与K之间的关系.(a) D = 10 m; (b) D = 15 m; (c) D = 20 mFig.8 Vertical bearing capacity factors of the pile–bucket composite foundations (NcV) with K: (a) D = 10 m; (b) D = 15 m; (c) D = 20 m

图9(a)为D20L10K2-V在竖向荷载达到竖向极限承载力时土体等效塑性应变云图，从图中可知土体在筒底尖端处塑性应变最大，此处土体最先开始破坏，且在筒与桩之间土体形成锥形破坏连通区.图9(b)为D20L10K2-V在竖向荷载达到竖向极限承载力时基础位移矢量图，从图中可知桩–筒复合基础在竖向荷载作用下呈锥形竖向刺入破坏模式.

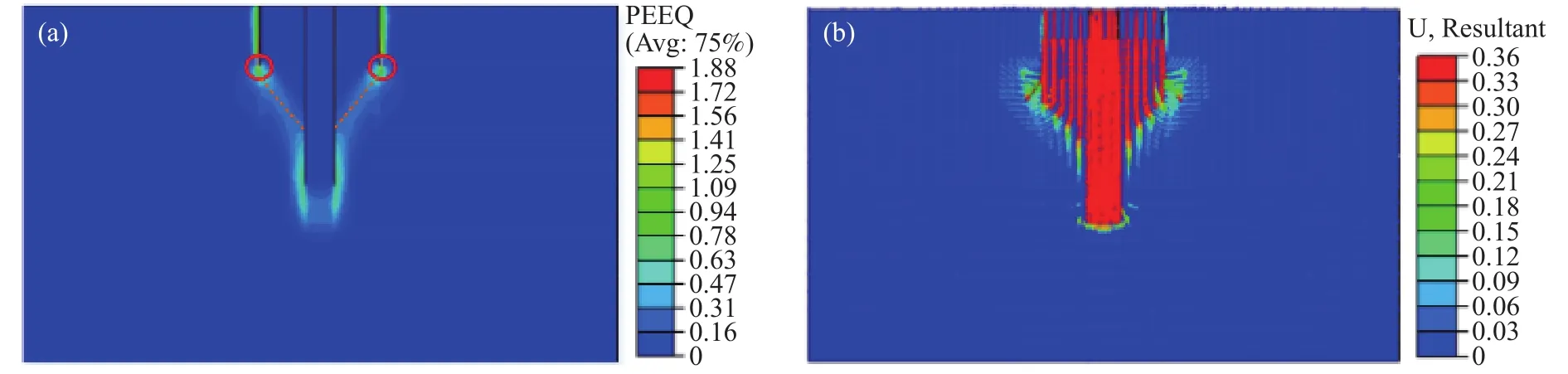
图9 竖向加载极限状态基础等效塑性应变云图(a)和位移矢量图(b)（D20L10K2-V）Fig.9 Equivalent plastic strain distribution (a) and displacement vector diagram (b) under the ultimate vertical bearing state

3.2 筒直径D和入土深度L对竖向承载特性的影响

图10为桩–筒复合基础竖向承载力系数与筒结构尺寸的关系图.图10(a)为D与NcV的关系图，图10(b)为L与NcV的关系图.图10(a)中NcV随着D增加逐渐变小；当L较小时，NcV与D之间为明显的曲线递减关系；当L较大时，NcV与D之间为曲线递减关系，但随着D增加，NcV减小趋势变缓.图10(b)中NcV随着L增加逐渐增加；当D为10 m和15 m时，NcV与L为线性关系.图11为桩–筒复合基础竖向承载力系数与D、L之间的三维关系图，图中可以看出当L/D较小时，NcV变化较小.研究结果表明D与L对桩–筒复合基础的NcV的影响存在交互作用关系.

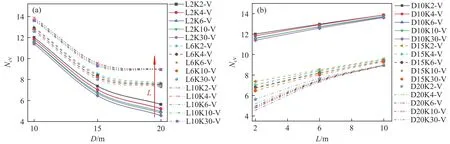
图10 桩–筒复合基础竖向承载系数NcV与D (a)和L (b)的关系Fig.10 Vertical bearing capacity factors of the pile–bucket composite foundations (NcV) with D (a) and L (b)

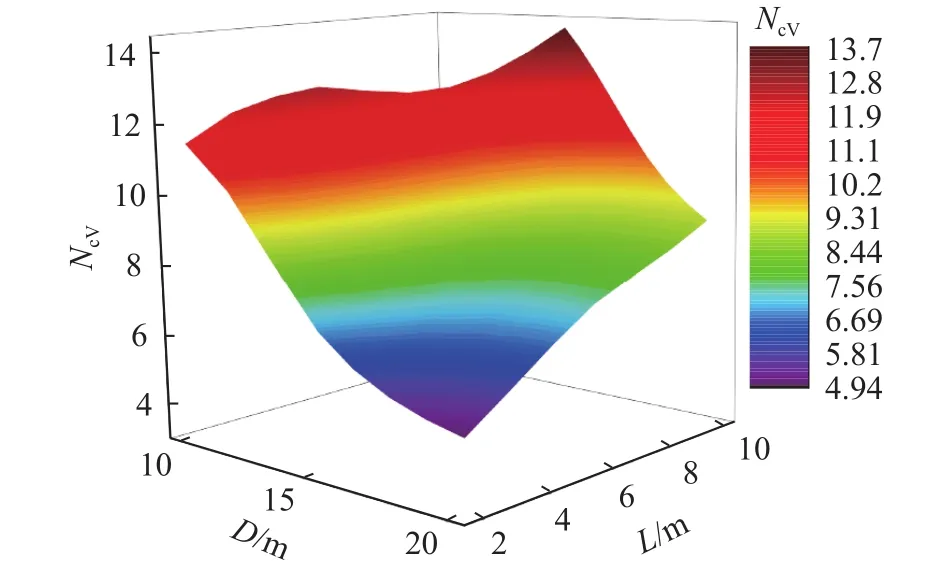
图11 D和L对竖向承载特性的影响Fig.11 Effect of D and L on vertical bearing capacity factors of pile–bucket composite foundations

4 桩–筒复合基础抗弯承载特性

4.1 系数 K对抗弯承载力系数的影响

同上两节相似，桩–筒复合基础的抗弯承载特性通过抗弯承载力系数值NcM描述，其中NcM=Mult/ADSu0.图12(a)、(b)、(c)分别为筒直径D=10、15、20 m时，桩–筒复合基础NcM与K之间的关系.从图中可以看出NcM与K之间为指数型关系，并随着K的增加逐渐减小.NcM与K之间的关系进行拟合，得到以下公式：

图12 桩–筒复合基础抗弯承载系数NcM与K之间的关系.(a) D = 10 m; (b) D = 15 m; (c) D = 20 mFig.12 Moment bearing capacity factors of the pile–bucket composite foundations with K: (a) D = 10 m; (b) D = 15 m; (c) D = 20 m

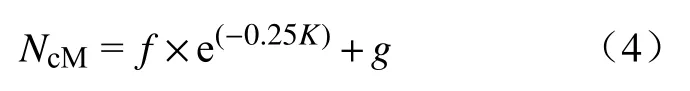
式(4)中系数f、g与筒结构尺寸相关，关系见图13.图13(a)所示f随着L的增加呈先增大后减小的趋势且随着D的增大而减小；图13(b)所示g随着L的增加呈线性增加且随着D的增大而减小.

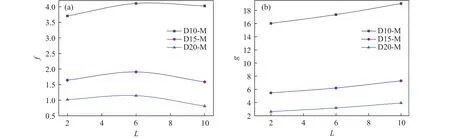
图13 公式(7)中的系数.(a) f; (b) gFig.13 Coefficients in Equation (7): (a) f; (b) g

4.2 筒直径D和入土深度L对抗弯承载特性的影响

图14为桩–筒复合基础抗弯承载力系数NcM与筒结构尺寸的关系.图14(a)为D与NcM的关系图，图14(b)为L与NcM的关系图.由图14(a)可知，NcM随着D增加逐渐减小；D相同时，NcM大小相近，且随着D增加，NcM逐渐向某一数值靠拢.图14(b)中NcM随着L增加呈线性增加.

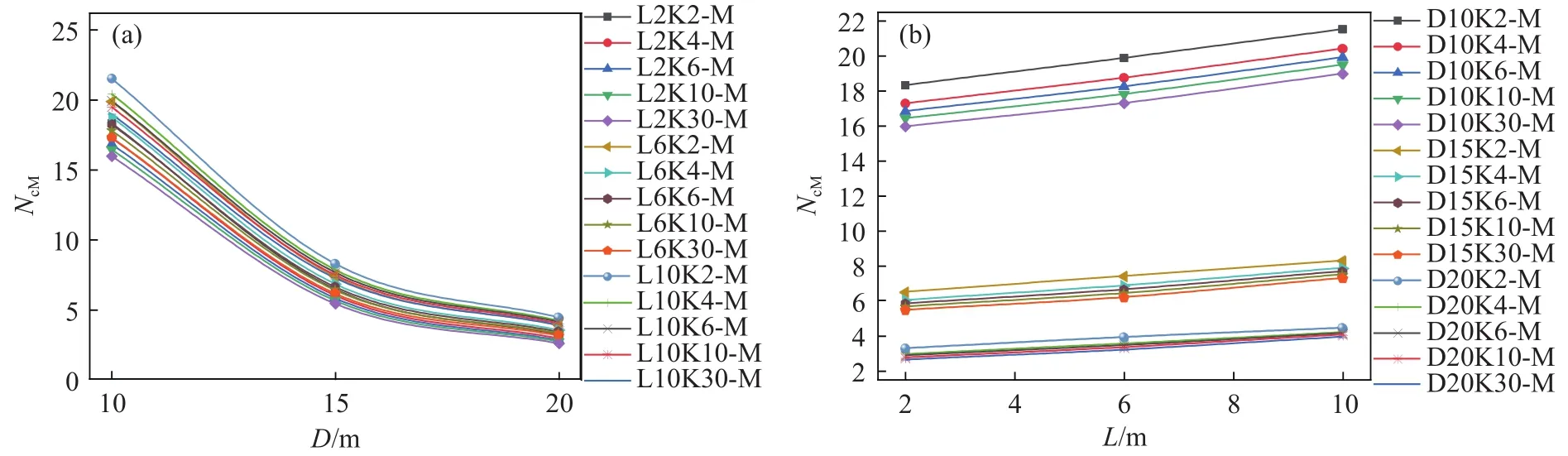
图14 桩–筒复合基础抗弯承载力系数NcM与D (a)和L (b)的关系Fig.14 Moment bearing capacity factors of the pile–bucket composite foundations with D (a) and L (b)

同水平承载力系数NcH的影响规律相似，D与L对桩–筒复合基础的NcM的影响也存在交互作用，且D对NcM的影响相对L的效果更为显著，如图15所示.

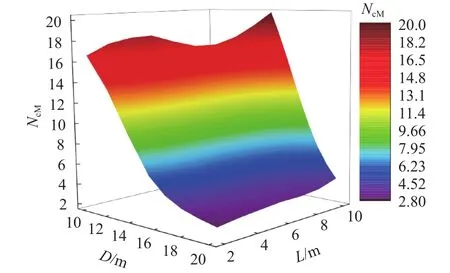
图15 D和L对抗弯承载特性的影响Fig.15 Effect of D and L on the moment bearing capacity factors of the pile–bucket composite foundations

5 影响因素的主次分析

正交试验法是一种可以安排多因素多水平试验的方法，根据均衡分布的思想，能够合理而高效地对影响因素进行分析.正交试验法具有正交性、均衡分散性以及综合可比性等特点，通过正交试验表可以合理试验，有效降低试验次数.正交试验法主要包含因素、水平和正交试验表[28].桩–筒复合基础的各向承载力系数与基础尺寸和饱和黏土非匀质特性有很大的关系，通过正交试验法对影响因素权重进行分析，为桩–筒复合基础在工程中的应用提供依据.

5.1 正交试验方案

本文正交试验通过合理安排影响因素大小，研究桩直径d、桩入土深度l、筒直径D、筒入土深度L以及黏土非匀质特性系数K对桩–筒复合基础水平承载特性、竖向承载特性和抗弯承载特性的影响.试验因素水平取4，即每种因素分别均匀取4个水平.因素水平表见表3.

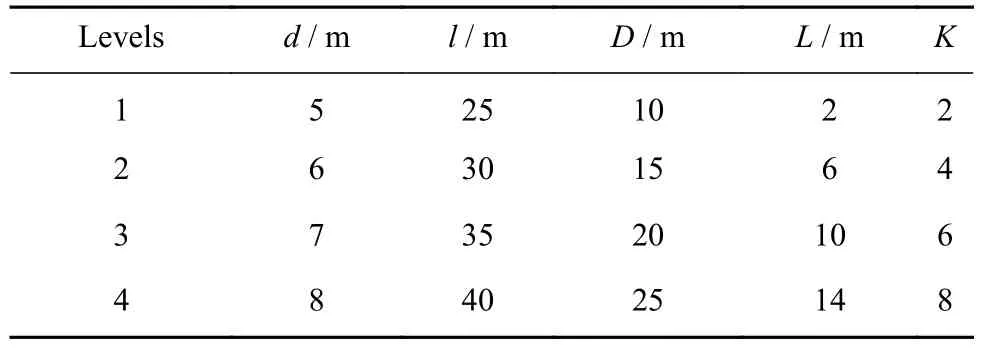
表3 因素水平表Table 3 Factors and levels

由因素水平表分析，根据正交试验表选取方法，选用L16(45)正交表.对正交试验表进行设计，得到正交试验方案，如表4所示.表4中前6列为正交试验方案，后3列为试验计算结果.

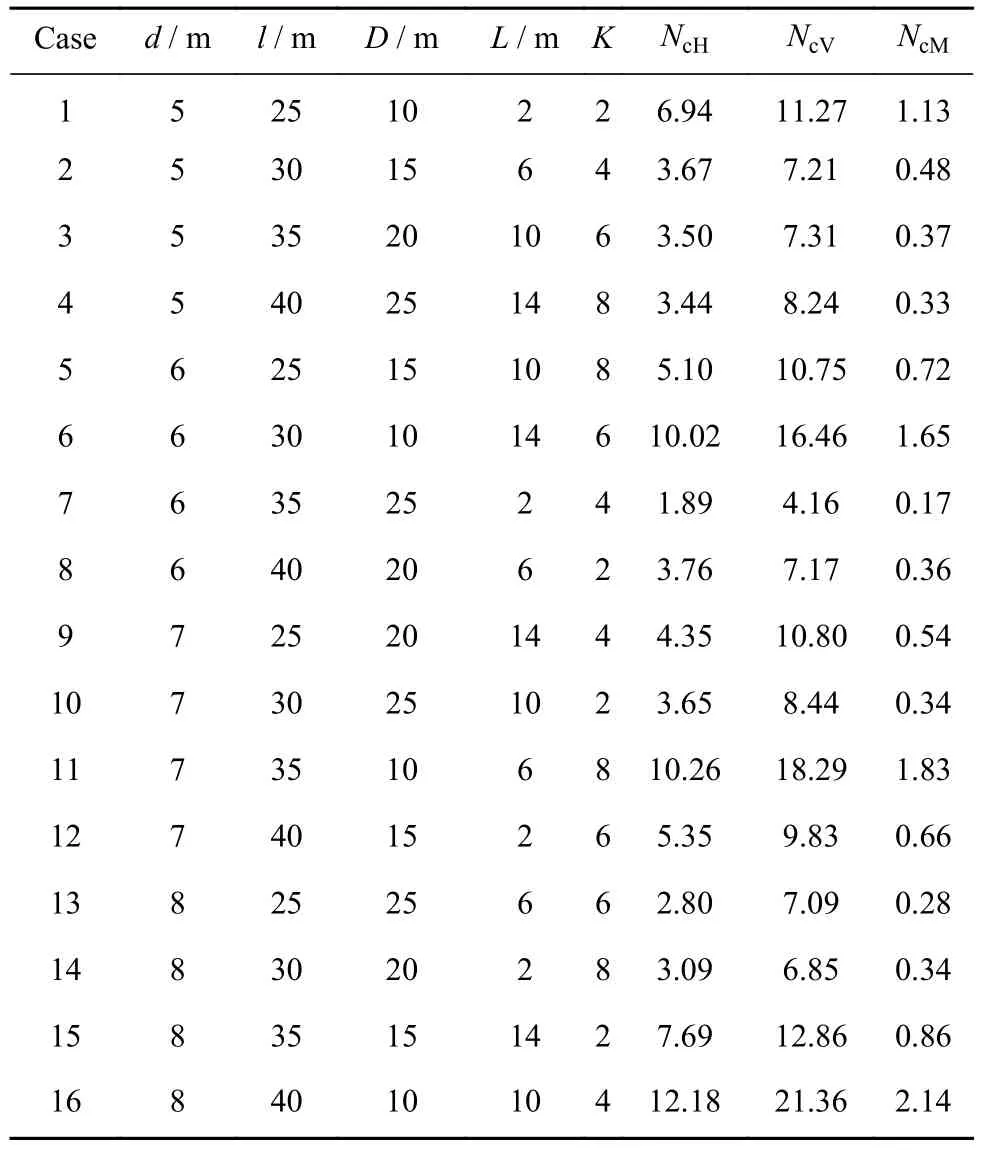
表4 正交试验方案及结果Table 4 Orthogonal scheme and results

5.2 结果分析

通过合理地分析正交试验结果，可以确定试验因素的主次、各试验因素的优水平及试验范围内的最优组合.极差分析法（R法）可以直观简便的分析试验结果，确定因素的主次.表5、表6和表7分别为对NcH、NcV、NcM的极差分析结果.上述表格中NcH（1）、NcH（2）、NcH（3）、NcH（4）分别代表各因素在不同水平时水平承载力系数NcH之和，R为不同因素的极差.

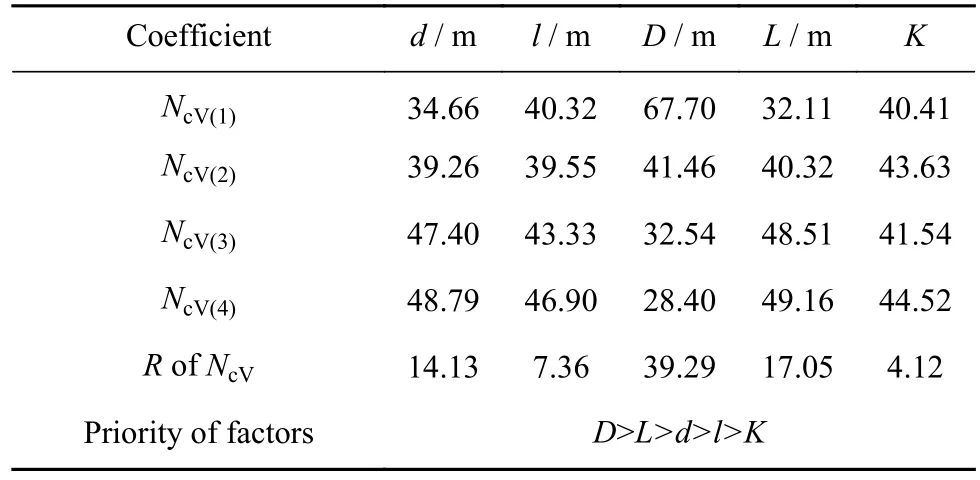
表6 竖向承载力系数NcV极差分析Table 6 Range analysis of NcV

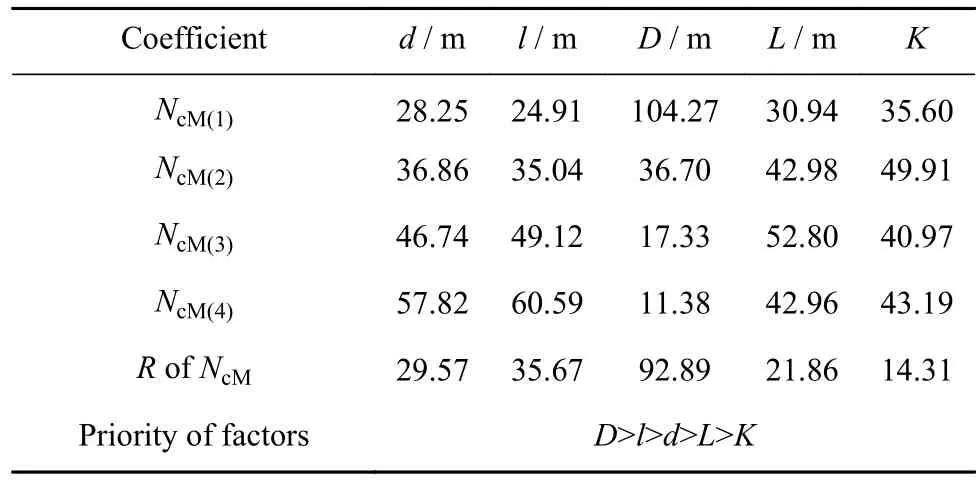
表7 抗弯承载力系数NcM极差分析Table 7 Range analysis of NcM

由表5可以看出，5个因素在4个不同水平时，对桩–筒复合基础水平承载力系数影响的因素从主到次的顺序为D>d>L>l>K.D对水平承载特性影响最大，D因素的影响极差为27.78，而其他影响因素对水平承载系数的极差都低于10.结果表明桩–筒复合基础的水平承载特性主要受横向尺寸（D和d）影响.

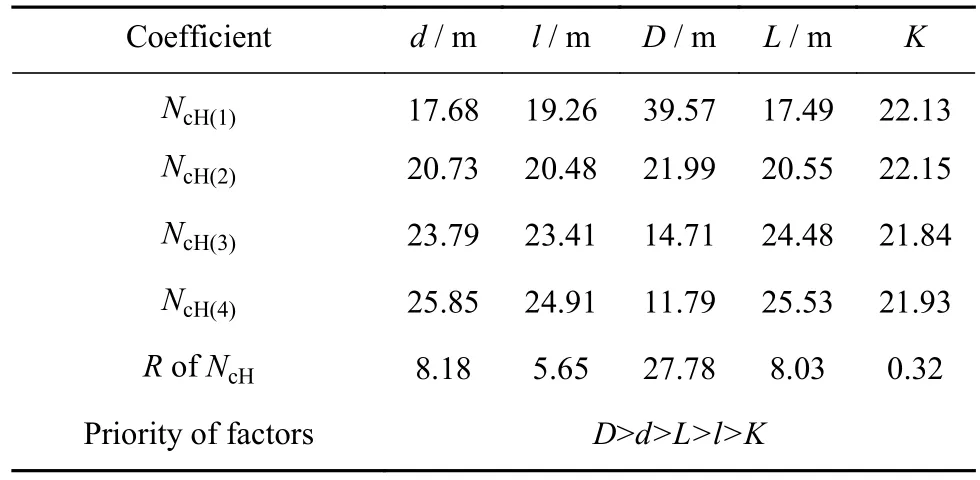
表5 水平承载力系数NcH极差分析Table 5 Range analysis of NcH

由表6可以看出，5个因素在4个不同水平时，对桩–筒复合基础竖向承载力系数影响的因素从主到次的顺序为D>L>d>l>K.桩–筒复合基础的筒直径D对竖向承载特性影响最大，D因素的影响极差为39.29，而其他影响因素对竖向承载系数的极差相对较小.结果表明桩–筒复合基础的竖向承载特性主要受筒结构尺寸（D和L）影响，对桩–筒复合基础竖向承载力进行设计时应优先考虑筒结构尺寸.

由表7可以看出，5个因素在4个不同水平时，对桩–筒复合基础抗弯承载力系数影响的因素从主到次的顺序依次为筒直径D>桩入土深度l>桩直径d>筒入土深度L>饱和黏土非匀质特性系数K.桩–筒复合基础的筒直径D对抗弯承载特性影响最大，筒直径D因素的影响极差为92.89，而其他影响因素对抗弯承载系数的极差相对较小.结果表明筒直径D对桩–筒复合基础的抗弯承载特性影响较大.

综上所述，筒直径D对桩–筒复合基础各向承载特性都有很大的影响，在单桩基础周围增加筒结构组成复合基础可以有效地提高基础的承载性能.

6 结论

本文考虑了饱和黏土非匀质特性系数K、筒结构直径D和入土深度L等因素，通过数值计算方法得到不同荷载作用下桩–筒复合基础的极限承载力，并转化为承载力系数，研究了筒结构尺寸对饱和黏土中桩–筒复合基础承载性能的影响，并通过正交试验法对桩–筒复合基础承载性能的影响因素进行分析，得到以下结论：

（1）筒结构尺寸对桩–筒复合基础的各向极限承载力系数影响较大，D和L对各向承载力系数的影响具有交互作用.

（2）K对竖向承载力系数NcV影响较小，并且随着筒结构入土深度增加，K对NcV的影响越小.水平承载力系数NcH和抗弯承载力系数NcM随K的增大而呈指数型减小.

（3）NcV、NcH和NcM随着D的增加而指数型减小，随着L增加而线性增大.

（4）正交试验结果表明，D对桩–筒复合基础承载性能的影响最大，而K的影响最小.在建造成本可控的条件下，增加筒结构直径是提高桩–筒复合基础的承载能力最有效的方式.