算术-几何平均的对数平均与正弦平均不等式
余 燕 翔
(浙江广播电视大学 平阳分校, 浙江 平阳 325400))
一、研究基础
设a,b>0且a≠b,则几何平均G(a,b),算术平均A(a,b),对数平均L(a,b),正弦平均Msin(a,b)和双曲正切平均Mtanh(a,b),以及高斯算术-几何平均AGM(a,b)的定义分别为:[1]1071-1092 [2]821-841
(1)
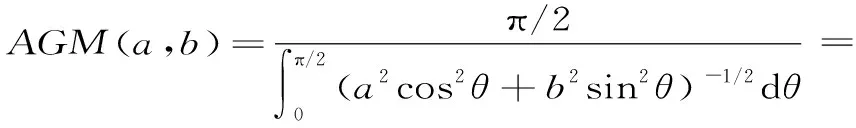
(2)
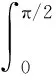
近年来,算术-几何平均,正弦平均和双曲正切平均,与其他经典平均及其组合的比较研究成果显著,国内外数学工作者发现了许多重要不等式.例如:
Vamanamurthy和Vuorinen证明了不等式
(3)
对所有a,b>0且a≠b成立,其中I(a,b)=(bb/aa)1/(b-a)/e是指数平均[3]155-166.
Alzer和裘松良证明了λ=3/4和μ=2/π,是使得下列双向不等式
对所有a,b>0且a≠b成立的最佳参数[4]289-312.
2015年,Witkowski证明了双向不等式
A(a,b) (4) 对所有a,b>0且a≠b成立[1]1 071-1 092. 组合不等式(3)和(4)可得下列不等式链: L(a,b) (5) 对所有a,b>0且a≠b成立. 根据不等式链(5),我们发现并证明了最佳参数α1,α2,β1,β2∈,使得双向不等式 对所有a,b>0且a≠b成立. 为证明本文的主要结果,我们首先需要以下基础知识和引理. 设r∈(0,1),第一类完全椭圆积分κ(r)和第二类完全椭圆积分ε(r)的定义为[5]43: 显然,函数rκ(r)在区间(0,1)内是严格单调递增的且值域为(π/2,+∞);函数rε(r)在区间(0,1)内是严格单调递减的且值域为(1,π/2),它们满足下列微分公式[6]474-475: 和Landen恒等式 引理1假设-∞ 也是单调递增(递减)的.如果f′(x)/g′(x)是严格单调的,则上述结论的单调性也是严格的[6]10. 引理2函数 在区间(0,1)内是严格单调递增的且值域为(π/4,+∞)[6]70. 引理3函数 在区间(0,1)内是严格单调递减的且值域为(2cos(1),3). 证明:微分φ(r)可得: (6) 其中, φ1(r)=-rr′2+(1+3r2)tan(r). 简单计算可得: φ1(0)=0, (7) (8) 由等式(6)(7)和不等式(8),使得 φ′(r)<0 (9) 对r∈(0,1)成立.注意到: φ(0+)=3,φ(1-)=2cos(1). (10) 所以,引理3容易从不等式(9)和等式(10)得到. 引理4函数 在区间(0,1)内是严格单调递减的且值域为(sech2(1),2). 证明:由微分γ(r)可得: (11) 其中, γ1(r)=-rr′2+2rr′2sinh2(r)+(1+3r2)sinh(r)cosh(r). 简单计算可得: γ1(0)=0, (12) (13) 由等式(11)(12)和不等式(13)可得: γ′(r)<0 (14) 对r∈(0,1)成立.注意到: γ(0+)=2,γ(1-)=sech2(1). (15) 所以,引理4容易从不等式(14)和等式(15)得到. 定理1双向不等式 对所有a,b>0且a≠b成立,当且仅当α1≤2/π和β1≥5/6. 证明:根据二元平均L(a,b),Msin(a,b)和AGM(a,b)是对称且一阶齐次的.不失一般性,假设a=1>b.设b=(1-r)/(1+r),r∈(0,1).则由等式(1)和(2)可得: (16) (17) 其中, 设f1(r)=tanh-1(r)-2rκ(r)/π,g1(r)=tanh-1(r)-sin(r),f2(r)=1-2ε(r)/π和g2(r)=1-r′2cos(r).简单计算,使得: f1(0+)=g1(0)=0,f(r)=f1(r)/g1(r), (18) (19) (20) 其中,φ(r)和φ(r)定义在引理2和引理3. (21) 定理2双向不等式 对所有a,b>0且a≠b成立,当且仅当α2≤2/π和β2≥7/8. 证明:不失一般性,假设a=1>b.设b=(1-r)/(1+r),r∈(0,1).则从等式(16)和Mtanh(a,b)=A(a,b)r/tanh(r)可得: (22) 其中, 设f1(r)=tanh-1(r)-2rκ(r)/π,h1(r)=tanh-1(r)-tanh(r),f2(r)=1-2ε(r)/π,h2(r)=r2+(1-r2)tanh2(r).则简单计算,使得: f1(0+)=h1(0)=0,g(r)=f1(r)/h1(r), (23) (24) (25) 其中,φ(r)和γ(r)定义在引理2和引理4. (26) 根据定理1和定理2可得推论1. 推论1双向不等式 对所有r∈(0,1)成立. 第一类完全椭圆积分κ(r)、第二类完全椭圆积分ε(r),以及算术-几何平均AGM(a,b)在数学、物理、力学和工程方面有很多应用.本文通过算术-几何平均与对数平均、正弦平均(或双曲正切平均)、调和组合的比较,给出了第一类完全椭圆积分κ(r)的反双曲正切与正弦(或双曲正切)函数的两个精确不等式.二、引 理
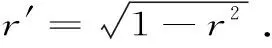
三、主要结果
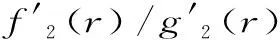

四、结 语

