无绝缘移频轨道电路在无砟轨道运用中的复线互阻抗计算

李智宇，阳晋，邹军

(1.石家庄铁道大学 交通运输学院，河北 石家庄，050043；2.北京全路通信信号研究设计院集团有限公司，北京，100073；3.电力系统及发电设备控制和仿真国家重点实验室，北京，100084)

无砟轨道由钢轨、道床和钢筋等构成，具有稳定性好、维修工作量少、使用寿命长和综合经济效益高等优点[1-4]，是我国高速铁路建设中的发展方向[5-6]。当客专区间存在四线并行线路时，邻线同频信号会通过空间耦合等方式在本区段形成干扰电流，该干扰可能会导致机车信号的误动作[7-8]。无绝缘移频轨道电路是高速铁路控制系统的重要组成部分，通过电路中的传输信号，用于自动、连续检测线路是否被机车占用，检查钢轨是否完整，保证行车的安全性[9]。钢轨阻抗是轨道电路中重要的电磁耦合参数[10-11]，尤其相邻线路间的互阻抗直接影响上下行线路间轨道电路信号和机车信号的安全性。因此，对其进行定量的计算分析，以正确设计轨道电路长度和防护措施，有重要意义。

对于轨道阻抗计算方法的研究，多数针对有砟轨道进行展开分析，主要包括有限元方法[12]以及通过推导得到的简化公式进行求解[13]。相比于有砟轨道，无砟轨道阻抗计算方法的研究相对较少。张汉花等[14]采用阻抗分解法结合有限元仿真进行了轨道电路的阻抗计算分析；张汉花等[15]结合有限元及电路方法，分析了频率、土壤电导率等参数对轨道阻抗的影响。以上均针对的是单线轨道阻抗的研究计算。杜学龙等[16]根据Carson 地阻抗简化公式即Deri 地阻抗公式推导得到了轨道互阻抗计算的简化计算公式，但该公式仅适用于路基无钢筋时复线轨道间的互阻抗计算，同时对轨道高度有一定的限制。

针对无砟轨道，其轨道结构复杂，同时轨道电路信号频率为1.7～2.6 kHz，此时，钢轨及钢筋内电流趋肤深度为毫米级。如采用有限元仿真计算，为保证趋肤效应计算结果的正确性，1个趋肤深度至少对应2层网格剖分。对于大空间、小尺寸的电磁场求解计算，当直接采用有限元仿真计算时，存在剖分单元数量大、求解收敛困难等问题。因此，为避免有限元建模计算的复杂性以及考虑钢筋对轨道阻抗的影响，需要针对复线无砟轨道间互阻抗的计算方法及其阻抗特性展开研究。

本文首先分别详细介绍用于求解复线无砟轨道互阻抗存在钢筋时的数值计算方法，同时介绍阻抗求解公式中涉及的无穷积分项的推导求解过程。其次，通过与有限元仿真结果进行对比，验证该数值计算方法的正确性。最后，以路基轨道为例，结合该数值计算方法，进行频率、土壤电导率、钢筋以及高度对互感的影响规律，并分析其影响程度。

1 计算方法简介

1.1 存在钢筋时的互阻抗计算

复线并行运行轨道模型横截面示意图如图1所示，无砟轨道结构主要包含钢轨、道床板、钢筋、混凝土底座。其中，道床板中埋有上、下2 层钢筋。与钢轨平行的钢筋为纵向钢筋，与钢轨方向垂直的钢筋为横向钢筋。单路钢轨和道床中纵横钢筋形成的钢筋网示意图如图2所示。

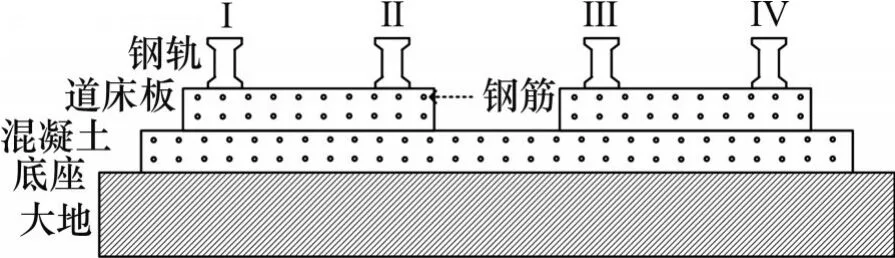
图1 复线并行轨道模型横截面示意图Fig.1 Cross section diagram of double track parallel track model

图2 单路无砟轨道钢轨与钢筋网简单示意图Fig.2 Simple schematic diagram of rail and steel mesh of single ballastless track

无砟轨道接地要求如下：

1) 纵向：将每股道整体道床最上层的钢筋中的3根纵向钢筋作为接地钢筋，即上层钢筋网中心1 根钢筋和最外侧2 根钢筋，钢筋直径为16 mm，纵向接地钢筋的混凝土保护层厚度不大于100 mm(一般不少于3根)。

2) 横向：为保证单点接地，每块道床内均设一处直径为16 mm 的横向接地钢筋，横向接地钢筋与纵向接地钢筋之间焊接。

3) 绝缘：接地钢筋与道床板内的其他结构钢筋交叉时需绝缘，不得构成接地闭合电气回路，原则上应对无砟轨道自轨底以下600 mm范围内的结构钢筋采取绝缘措施(绝缘套管和绝缘涂层等)。

4) 接地单元：沿线路方向每100 m形成一个接地单元，一个接地单元内的道床板间通过不锈钢缆线连接，每一个接地单元与接触网架空地线连接一次，同一接地单元内，应设且仅设1根横向钢筋与3根纵向接地钢筋焊接。存在道床横向结构缝时，在结构缝划分的每个道床板内，应设且仅设1根横向钢筋与3根纵向接地钢筋焊接。

根据以上接地要求可知：上层道床板中有接地的钢筋，混凝土底座中钢筋不接地且采用绝缘措施。

经分析，横向钢筋对互阻抗的影响可忽略，本文只考虑纵向钢筋对互阻抗的影响，钢筋不特殊介绍时，即默认为纵向钢筋。

假设图1中钢轨由左到右分别编号为Ⅰ，Ⅱ，Ⅲ和Ⅳ号钢轨，由Ⅰ号和Ⅱ号钢轨构成回路1，Ⅲ号和Ⅳ号钢轨构成回路2，轨道间的互阻抗即回路1 和回路2之间的互阻抗。在Ⅰ号、Ⅱ号钢轨上分别通入电流Irail和-Irail，则有互阻抗Zm：

式中：Em为回路1中通入电流后在回路2中建立的感应电动势。由电磁感应可知，当钢轨Ⅰ号、Ⅱ号中通入钢轨信号电流时，钢筋中将产生感应电流，若设钢筋总根数为n，对应的钢筋电流为Ij(j=1，…，n)。对以大地和各钢筋形成的回路列方程，有

式中：Zjj(j=1，…，n)为钢筋的自阻抗，包括内自阻抗和外自阻抗2 部分；Zij(i，j=1，…，n)为钢筋之间的互阻抗，Zij=Zji；ZjⅠ和ZjⅡ分别为各个钢筋与Ⅰ号、Ⅱ号钢轨之间的互阻抗。由该方程便可求解得到各个钢筋中电流Ij。

综合以上可知，式(1)中的感应电动势Em是钢轨电流Irail和钢筋电流Ij(j=1，…，n)共同作用的结果，即Em为

式中：Em1为钢轨电流±Irail在回路1 上产生的感应电动势；Em2为各个钢筋电流Ij在回路2上产生的感应电动势。Em1和Em2分别为：

式中：ZⅢ,Ⅰ，ZⅣ,Ⅱ，ZⅣ,Ⅰ和ZⅢ,Ⅱ为对应钢轨与钢轨之间的互阻抗；ZⅢj和ZⅣj(i，j=1，…，n)分别为j号钢筋与Ⅲ号、Ⅳ号钢轨之间的互阻抗。

结合式(1)和式(3)～(5)，可求得轨道间的互阻抗Zm。

综合以上各式可知，求得轨道间互阻抗的关键在于求解钢轨和钢筋任意2 个导体之间的互阻抗，该互阻抗为任意2个导体分别与大地形成的回路之间的互阻抗。其求解可采用考虑大地存在情况下的Carson 地阻抗计算公式[17]计算，模型参考图如图3所示，大地上方2个导体之间的互阻抗Z12计算公式为：

图3 大地上方两导体系统Fig.3 Two conductor system above earth

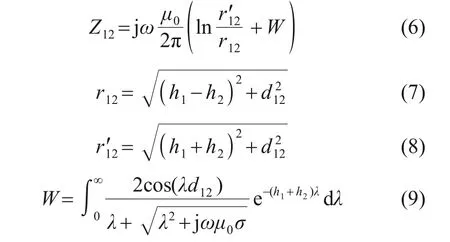
式中：j为虚数单位；ω为信号角频率；μ0和σ分别为大地磁导率和电导率；h1和h2分别为1号导体和2号导体距离大地的高度；d12为2个导体之间的水平距离；r12为1号导体和2号导体之间的距离；为1号导体和2号镜像导体之间的距离；W为大地为有限电阻率时的修正项；λ为积分变量。

由式(9)可以看出，修正项W为无穷积分项，存在求解困难的问题。目前存在的求解方法是针对该项进行假设条件下的公式简化，最经典的为Deri地阻抗计算公式[18]。但结合式(9)和文献[16]可知，基于Deri 地阻抗公式对计算轨道互阻抗时，对于轨道高度具有一定的限制，不足以满足轨道互阻抗计算的应用场景。

为此，本文基于Carson 地阻抗计算公式中的原始积分项W，提出采用AET (asymptotic extract technique)方法[18]进行无穷积分项的求解。

1.2 基于AET方法计算W

令参数γ2=jωμ0σ，式(9)可转化为

令被积函数用F(λ)表示，即

根据AET 方法，将以上无穷积分进行截断，取截断值T=10|γ|，则式(10)转换为

由此可知，第一项W1可采用常规积分法进行求解，第二项W2计算时需进行特别处理。首先结合泰勒展开和换元积分法对被积函数F(λ)进行化简，经化简后W2转化为

式中：ξ为换元后的积分变量。

经化简后，第二项W2的计算则可根据指数积分公式直接调用进行计算。在区间[0，T]中，由于T很小，计算时没有振荡现象，可根据cos(λd12)的零点分区间，每个区间采用自适应高斯-勒让德积分函数quadgk进行数值积分计算即可。

根据式(6)和式(15)计算得到两导体之间的互阻抗后，结合式(1)和式(3)～(5)，便可进行有钢筋时轨道间互阻抗Zm的求解计算。

2 计算方法准确性验证

多物理场耦合计算软件Comsol 是一款基于有限元的仿真软件，可进行复杂结构多种介质情况下的电磁场仿真计算。为与仿真方法相区分，以下简称本文所提出的方法为数值计算方法。因此，为验证本数值计算方法结果准确性，可基于该软件进行仿真计算，并进行两者计算结果的对比分析。

由于横向钢筋基本不起作用，所以数值计算方法中未考虑横向钢筋的影响是合理的，这点可通过三维情况下仿真计算进行说明。

2.1 横向钢筋下的三维仿真计算

为分析横向钢筋对阻抗的影响，现围绕横向钢筋展开计算分析。计算模型为：大地上方存有一通电钢轨，道床板中包含4根纵向钢筋，分别进行无横向钢筋和布置2 根、4 根横向钢筋3 种不同情况下的电磁场计算，横纵向钢筋相互绝缘。道床板中包含4根纵向钢筋和4根横向钢筋时的模型图如图4所示。钢轨上施加电流信号，与钢轨同向的x方向为纵向，与钢轨方向垂直的y方向为横向。

图4 横向钢筋影响分析模型Fig.4 Analysis model of influence of transverse reinforcement

取与钢轨同平面的纵向直线为磁场参考观察处，计算得到的磁密相对误差如图5所示。横向钢筋数分别为2根和4根时钢筋电流密度分布图如图6所示。

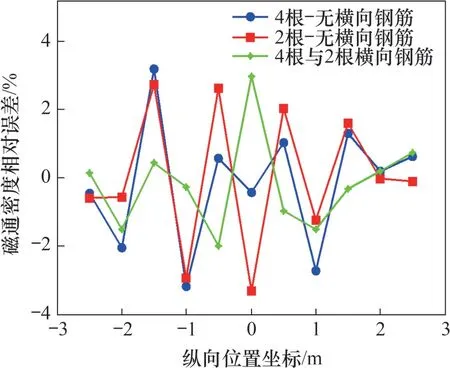
图5 有无横向钢筋时磁通密度的相对误差Fig.5 Relative error of magnetic flux density with and without transverse reinforcement

由图5 可以看出：当横向钢筋分别为4 根和2根时，两者与分别没有横向钢筋时计算得到的磁密相对误差均在4%以内，说明有横向钢筋时和没有横向钢筋时的磁场计算结果基本一致；同时，由4根横向钢筋和2根横向钢筋之间的磁密相对误差可以看出，除了位于x=0 中心处相对误差约为3%以外，其他位置处的相对误差基本在2%以内，说明横向钢筋数增加时基本不影响电磁场计算结果。再者，结合图6可以看出，钢筋上的感应电流基本均分布在靠近钢轨的中心2根纵向钢筋上。

图6 横向钢筋电流密度分布Fig.6 Current density distributions of transverse reinforcement

综合以上说明，横向钢筋影响不大，计算分析时可不考虑横向钢筋的影响。轨道阻抗计算时三维模型可简化为二维模型进行计算分析。因此，结合以上分析，利用Comsol 建立路基二维模型，通过仿真计算验证本文所提出的互阻抗数值计算方法的准确性。

2.2 仿真计算和数值方法计算结果对比验证

由文献[16]可知，互阻抗中电阻比较小，所以计算分析时主要侧重于互感的计算大小。已知单路两钢轨之间的距离为d=1.435 m，两路轨间距D=5 m，钢轨距离大地的高度h=0.5 m，频率为1 700 Hz，道床板中分别布置上、下2 层钢筋，每层钢筋为10根。左侧轨道中通入1 A电流，由此计算在相邻轨道中产生的互感。为简化仿真计算，钢轨采用圆导体代替，路基情况下复线轨道仿真模型如图7所示。对于高架桥上复线轨道间互感的计算，需要将道床板和轨道距离地面高度增加高架桥面的高度。计算得到的有钢筋时仿真结果和数值计算结果如图8所示。图8中，Comsol软件采用有限远方法，其需要截断无限远边界；而本文方法是考虑了无限远处的自然边界条件的，因此，有限元方法计算结果会偏小，这是合理的。

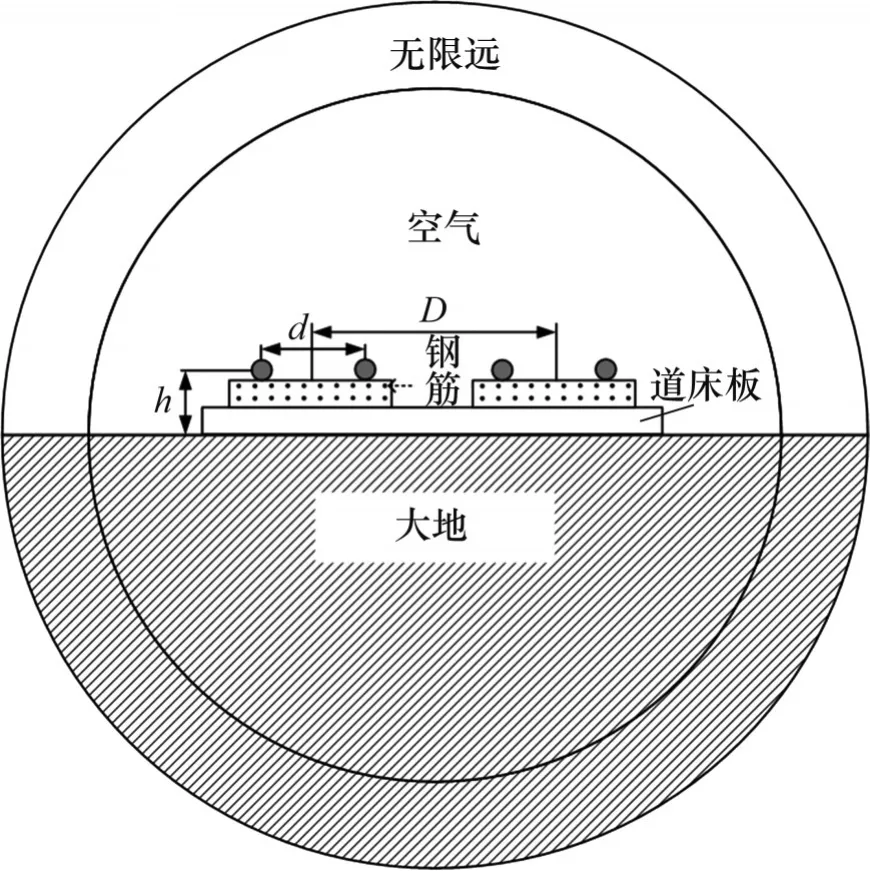
图7 路基情况下复线轨道仿真模型Fig.7 Simulation model of double track at subgrade condition

图8 互感仿真结果和数值结果对比Fig.8 Comparison between simulation results and numerical results of mutual inductance

由图8可知：基于数值计算方法和有限元仿真计算分别得到的互感随频率的变化曲线相对误差不大于2.6%，说明数值计算方法是有效的，可用于后期频率、土壤电导率等参数的影响分析，避免了仿真计算的复杂性以及网格剖分带来的计算量大的问题。

3 不同参数对轨道电感影响

以图7所示的路基复线轨道模型为例，进行频率、土壤电导率、钢筋和轨道高度对复线轨道间互感的影响规律及影响程度分析。为此，各部分的材料属性初始设置如表1所示，结构尺寸布置如表2所示。

表1 材料参数Table 1 Material parameters

表2 结构尺寸Table 2 Structural dimensions

3.1 频率和电导率对互感影响

假设道床板中存在钢筋，计算不同频率下复线轨道间的互感。由于轨道电路中的信号频率为1 700～2 600 Hz，因此，设置频率分析范围为1 500～3 000 Hz。计算得到的随频率变化的互感曲线如图9所示。

图9 有无钢筋时不同频率下的互感Fig.9 Mutual inductance at different frequencies with and without reinforcement

由图9可以看出：当道床板中有钢筋时，互感随频率增大逐渐减小，此时互感最大变化率为31.81%。这是由于涡流效应在钢筋中产生了相反的感应电流，起到了去磁作用。另外，频率越大，去磁作用越强，从而导致频率越大，互感越小。当道床板中没有钢筋时，互感最大变化率为0.05%，电感基本无变化。说明当存有钢筋时频率对互感的影响较大，无钢筋时频率对互感基本无影响。

3.2 土壤电导率对互感影响

土壤中的水分和盐分会影响土壤电导率。当土壤含水率为10%～30%时，土壤的电导率变化范围为0.01～0.16 S/m；对于含有盐分的土壤，电导率变化较大。不同水分和盐分时的电导率如表3所示。

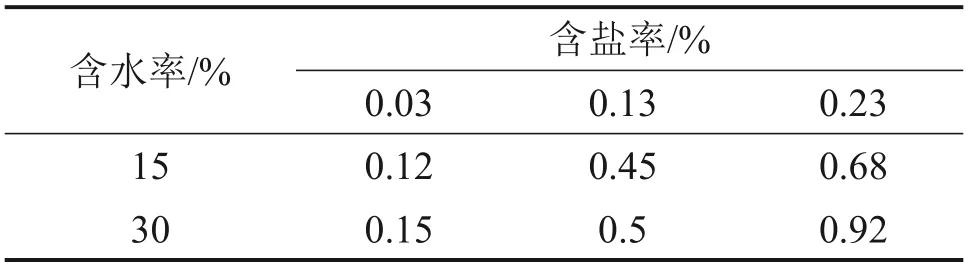
表3 土壤不同含水率和含盐率时的电导率Table 3 Electrical conductivity of soil with different moisture and salinity S·m-1

因此，为考虑土壤基本不导电的极限情况，土壤电导率分别取为0.000 1，0.001 0，0.010 0，0.100 0 和1.000 0 S/m。计算得到有钢筋时不同电导率下互感随频率的变化曲线如图10所示。

图10 有钢筋时不同电导率下的互感Fig.10 Mutual inductance at different conductivities with reinforcement

由图10 可知：当土壤电导率为0.000 1～0.100 0 S/m 时，随电导率逐渐增大，互感逐渐减小，这是由于电导率越大，大地涡流作用导致的大地的去磁作用越强；当电导率为1.000 0 S/m，同时频率在较高范围内时，此时的互感比电导率为0.010 0 S/m 下的互感大，出现这种现象的原因可能是电导率和频率越大，大地中的感应电流越大，且电流分布越集中在大地表面，距离钢筋越近，两者中感应电流的相互作用可能导致去磁作用减弱。

综合不同土壤电导率时的互感大小发现，当电导率为0.000 1～1.000 0 S/m时，互感的最大变化率为2.45%，这表明土壤电导率对复线轨道间互感基本无影响。

3.3 钢筋对互感的影响

由3.1 节有钢筋情况下的频率分析结果可知，钢筋具有去磁作用，因此详细分析钢筋对互感的影响程度。根据钢筋的布置情况，分析钢筋布置位置对互感的影响，进行以下4 种情况下的互感计算：

1) 道床板中上下2层均布有钢筋，简称为有钢筋的情况；

2) 无钢筋时的互感计算；

3) 靠近激励的左侧道床板中存在钢筋、右侧无钢筋；

4) 道床板中仅布置上层钢筋时的互感计算。计算结果分别如图11 所示。由图11 可以看出：当无钢筋时，互感约为17.21 μH/km，有钢筋时互感小于3 μH/km。由此可知，有无钢筋对复线轨道间互感的影响较大。

图11 不同频率下有无钢筋时的互感Fig.11 Mutual inductance with and without reinforcement at different frequencies

不同频率下仅左侧道床板中存在钢筋时的互感均值约为7.71 μH/km；道床板中仅存在上层钢筋时的互感均值约为8.42 μH/km；对比无钢筋时的互感，一方面说明道床板中上、下2层钢筋对于互感具有基本相当的去磁作用；另一方面说明左、右两侧的钢筋对于互感也基本具有相同的影响程度，即使是在左侧轨道中通入电流信号，右侧道床板中的钢筋相比于左侧钢筋距离激励源较远，但是同样起到了去磁作用，其影响不可忽略。

3.4 轨道高度对互感的影响

高速铁路不仅有路基的情况，还存在高架桥上高铁运行的情况。因此，进行轨道高度对复线轨道间互感的影响分析。设轨道高度(包括桥梁高度)H=0～50 m。其中，当H=0 m时，相当于路基轨道高度的情况。同时考虑道床板中有无钢筋的情况，计算得到的不同高度下有无钢筋时互感及有钢筋时的互感如图12所示。

图12 不同高度时的互感Fig.12 Mutual inductance at different heights

由图12 可以看出：不论有、无钢筋，互感基本不随高度变化而变化，说明高度对于复线轨道间的互感基本无影响。

4 结论

1) 当道床板中无钢筋时，频率对互感几乎无影响；有钢筋时不同频率下互感的最大变化率为31.81%，相比于无钢筋的情况，有钢筋时频率对互感的影响较大。

2) 当道床板中有钢筋时，土壤电导率为0.000 1～1.000 0 S/m 时互感的最大变化率为2.45%；当轨道高度在0～50 m 时，互感为2.73～2.74 μH/km，说明在有钢筋时土壤电导率和轨道高度对互感几乎无影响。

3) 在同频率下无钢筋时，互感约为17.21 μH/km，有钢筋时互感小于3 μH/km，明显比无钢筋时的互感小，说明钢筋的有、无对互感影响较大；与无钢筋时的互感相比，当道床板中分别仅有上层钢筋和左侧钢筋时，互感最大变化率均超过50%，说明道床板中的不同位置处的钢筋均影响互感。

4) 无砟轨道线路轨道电路互感参数测试时，应按照1 700，2 000，2 300和2 600 Hz这4种轨道电路工作频率分别测试；无砟轨道线路轨道电路邻线干扰耦合计算时，无须考虑土壤电阻率影响，可极大简化计算模型和提升计算效率；轨道电路运用于无砟轨道线路时，因互感耦合系数较大，应考虑适当缩短上、下行轨道电路区段的并行长度。