基于电涡流传感器的机床导轨运动误差在机测量方法*
殷 骁,张记云,娄志峰
(大连理工大学机械工程学院,辽宁 大连 116024)
0 引言
直线导轨是数控机床、坐标测量机等高精密加工与测量设备的重要组成部分。其运动误差是影响上述设备精度的主要因素[1]。通过测量导轨运动误差并进行误差补偿,对提高机床的加工准确度有重要意义。根据ISO 230-1[2],导轨运动副在移动时会产生6个自由度的误差,即定位误差(δz)、水平直线度误差(δx)和竖直直线度误差(δy)、滚动角误差(εx)、偏摆角误差(εy)、俯仰角误差(εz)。传统的几何误差检测仪器,如水平仪、激光干涉仪等,一次只能测单项或两项误差。要获得6个自由度误差,需要多个仪器对导轨进行多次测量。为了提高测量效率,国内外研究学者提出了多种导轨多自由度误差同时测量的方法。例如,张忠宁[3]、Yang L[4]、Barka N[5]提出基于激光准直原理的多自由度测量方法,以激光作为参考基准,通过分光镜获得多束平行光,光线沿特定的光路传播,导轨带动移动端运动,根据入射光斑在光电传感器表面的位置变化,计算出多自由度误差。基于激光的测量方法精度高、测量方便,但是存在光源发热引起光束的漂移[6]、抗干扰能力差等缺点。除了采用激光作为测量基准,亦有学者采用了其他传感器测量平台的运动误差。Zhao B[7]设计了一种由霍尔传感器组成的三自由度测量系统,能测量光刻机短行程工作台的X、Y位移以及绕Z轴的旋转角度θZ。Lee 等[8]基于电容位移传感器设计了一套多自由度测量装置,能够同时测量直线运动平台6个运动误差中的5项(定位误差除外)。
以上方法大多都是在机床处于非加工状态下的离线测量,然而实际工况下的直线导轨会因载荷、温度等因素产生难以预测的形变。Wei G[9]利用电容传感器、激光干涉仪与准直仪进行了商用精密工作台运动误差的在机测量实验。Zhao L[10]利用线性光栅系统和柔性机构构建了一种新型探头,并搭建了多步式测量系统,通过多探头误差分离算法,在机测量出直线导轨的运动误差。但上述两种方法需要采用精密基准,或应用于对环境有较高要求的装备测量。
电涡流传感器具有高性能、抗干扰强、成本低、非接触等优点,广泛应用于工业领域中进行位移测量[11]。本文提出了一种基于电涡流传感器的导轨运动误差在机测量方法和系统,相比激光和其他传感器,电涡流传感器受环境因素的影响很小,非常适合用于机床在机测量。该系统结构简单,不需要超高精度测量基准,可同时测量直线导轨的直线度、滚动角。通过与标准仪器的静态和动态对比实验,验证了此方法的测量的准确性,为多自由度在机测量系统的发展提供了研究基础。
1 结构设计与测量原理
1.1 电涡流传感器工作原理
电涡流位移传感器的测量原理如图1所示。其测量原理基于电涡流效应,属于电感式测量,它由探头、前置器、连接电缆组成。工作时,探头内线圈通过交变电流I1,形成交变磁场H1。根据电磁感应定律,靠近磁场H1的金属导体会在表面产生感应电涡流I2,同时这个电涡流也会产生一个与H1方向相反的磁场H2,H2会使得探头内线圈的阻抗值发生改变。阻抗值的变化与被测物到探头之间的距离直接相关。探头连接到前置器后,前置器将阻抗变化量转换为电压信号v。信号采集卡采集电压信号v,通过公式1即可获得该电涡流探头的位移量x。
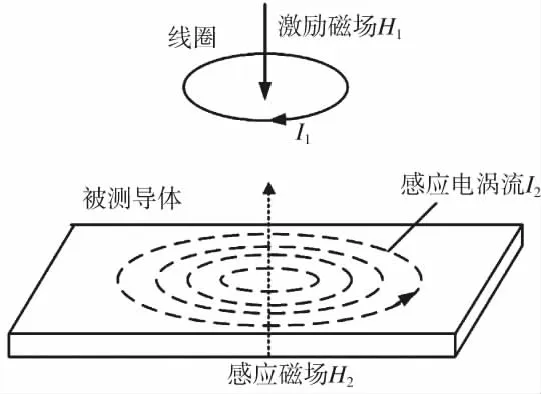
图1 电涡流传感器的测量原理
x=k(v-b)
(1)
式中,k为灵敏度,通过标定实验获得;b为初始电压值。
1.2 结构设计

图2 多自由度测量系统
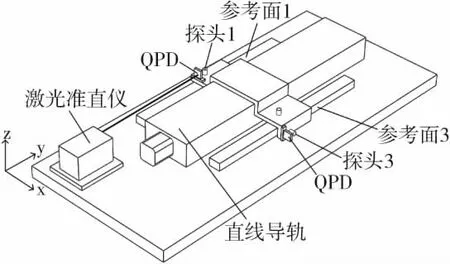
多自由度测量实验平台的设计如图2所示,包括伺服电机、直线导轨、运动平台和测量系统。测量系统由3个电涡流传感器和两根参考基准组成,能够同时测量3个自由度的误差。参考基准的作用是为电涡流探头提供参考面,其采用殷钢制造,具有热膨胀系数极低的特点。电涡流探头1与参考面1用来测量运动平台的竖直直线度,探头3与参考面3用于测量水平直线度。探头1、2以及参考面1、2组成滚动角误差测量单元,其中两探头的距离为L。当电机驱动平台移动时,由于存在误差运动,探头与参考面的位置发生相对变化,经过理论模型计算分析,可以同时得到导轨3个自由度误差。
1.3 直线度测量原理
测量时,运动平台带动探头扫过参考面。被测导轨上平台的几何运动误差通过探头相对于参考面的位移变化量Δx′n(i)反映出来。Δx′n(i)的计算公式如下:
Δx′n(i)=xn(i)-xn(0)
(2)
其中,xn(i)表示第n号(n=1,2,3)探头在位置i处的位移读数,Δx′n(i)表示探头n在位置i处的相对于初始位置(xn(0))的变化量。
作为测量基准的参考表面理论上不存在平面度误差,然而,由于加工水平的限制,实际参考面存在几何形状偏差。由此带来的误差称参考面误差δr(i)。如图3所示。
在位置i处,实际参考面与理想参考面偏差为δr(i)。第n(n=1,2,3)号探头在位置i位移的真实值为x′n(i):
x′n(i)=xn(i)-δr(i)
(3)

图3 参考面误差
所以,去除参考面误差后,由导轨运动误差导致位置i处探头位移变化量Δxn(i)为:
Δxn(i)=Δx′n(i)-δr(i)
(4)
导轨直线度误差是指实际被测直线要素相对其理想直线的最大的变动量。直线度的测量原理如图4。

图4 直线度测量原理
以参考面1、3作为测量的基准,运动平台带动探头首尾往复运动,进行初值校准,使得探头在首尾读数为0。若导轨存在直线度误差,电涡流探头与参考面的距离将会发生改变,探头读数发生变化。探头1、3在初始位置读数为x1(0)和x3(0),当运动到位置i时,读数为x1(i)和x3(i)。位移变化量Δx1(i)与Δx3(i)即代表导轨竖直直线度δy与水平直线度δx。
1.4 滚动角测量原理
滚动角的测量原理如图5所示。滚动角测量单元由传感器1与2组成,两者的距离为L。当导轨存在滚动角误差时,两探头之间在位置i处的读数差Δx2(i)-Δx1(i)将会发生改变。
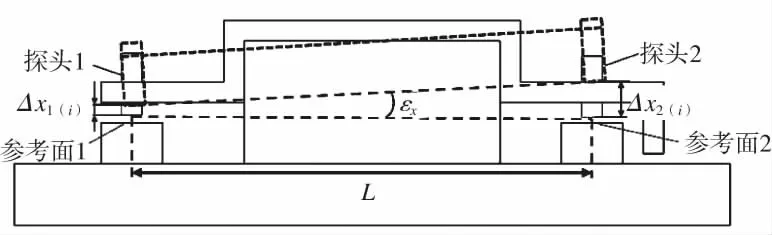
图5 滚动角测量原理
不考虑参考基准初始安装平行度误差时,滚动角误差εx(i)可跟据公式(5)得到。其中,传感器的分辨率为固定值0.1 μm,因此滚动角测量的分辨率是由距离L确定的(εx=x/L),当L=230 mm,分辨率为0.1″。
(5)
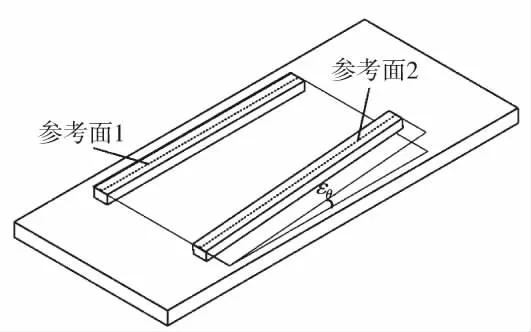
图6 参考基准安装平行度误差
滚动角测量时需要考虑到两个参考基准的安装平行度误差。理想状态下,两根参考基准安装时应该平行且处于同一平面。实际安装如图6所示,两参考面存在一个误差大小为εθ的夹角。
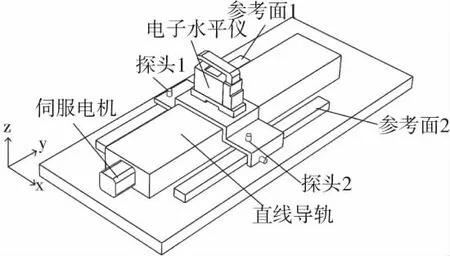
因此,实际测量得到的滚动角误差ε′x(i)包含了直线导轨的滚动角误差θr(i)和参考基准安装平行度误差εθ。因此,在测量滚动角之前,需要先设计实验测量出夹角εθ。在直线导轨上选取几个测量点,利用电涡流探头1、2和水平仪同时测量滚动角,探头测量值与水平仪测量值的差值即为参考基准安装平行度误差εθ,如公式(6)所示。
εθ=ε′x(i)-θr(i)
(6)
式中,ε′x(i)是依据公式5计算的导轨滚动角探头测量值,θr(i)为水平仪测量的滚动角值。对于直线导轨真实滚动角测量,公式(5)可进一步修正为:
(7)
2 测量实验
2.1 传感器标定实验
在测量之前,需要重新对电涡流探头(米朗ML33,量程1 mm,分辨率0.05 μm)进行标定。标定所用的校准仪器为精密手动Z轴升降台、数显电感测微仪(瑞士SYLVACD62S,分辨率0.01 μm)、转接板。标定示意图如图7。

图7 标定实验
标定的范围为±100 μm,以探头的输出电压为横轴,电感测微仪示数为纵轴,用最小二乘法对数据进行拟合,则直线的斜率就是探头的灵敏度K。最终标定结果如图8所示。由标定结果可知,标定残差均在±0.7 μm以内。
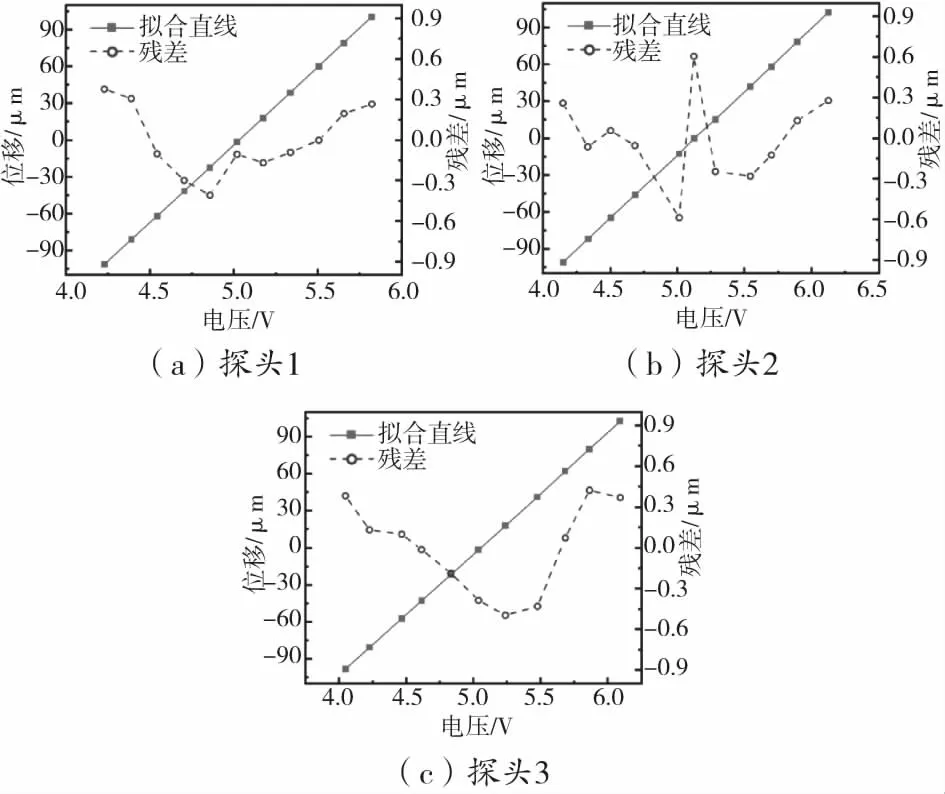
图8 各探头标定结果
2.2 误差对比实验
为了验证所提出方法的正确性,搭建了如图9所示的在机测量实验平台。其中包括伺服电机、线性导轨、运动平台、3个电涡流传感器、2根研磨过的高精度参考基准(长度450 mm)。为了防止参考基准安装过程中,由于安装面的平面度较差导致参考基准产生形变,进而影响探头的读数,实验中将参考基准首尾用螺栓和垫片将其悬空固定。

图9 多自由度测量系统
为了测量参考面对电涡流探头读数的影响,在参考基准安装到平台前先在坐标测量机上进行了参考面误差的测量实验。测量方式是:将基准固定在大理石平台上,探头安装于测量机的Z轴,Z轴带动探头扫过参考面,可以得到参考面偏差。为了便于测量,在参考基准上设置了初始点,保证基准安装到实验平台和坐标测量机的起始位置相同。测量过程如图10。

图10 测量实验
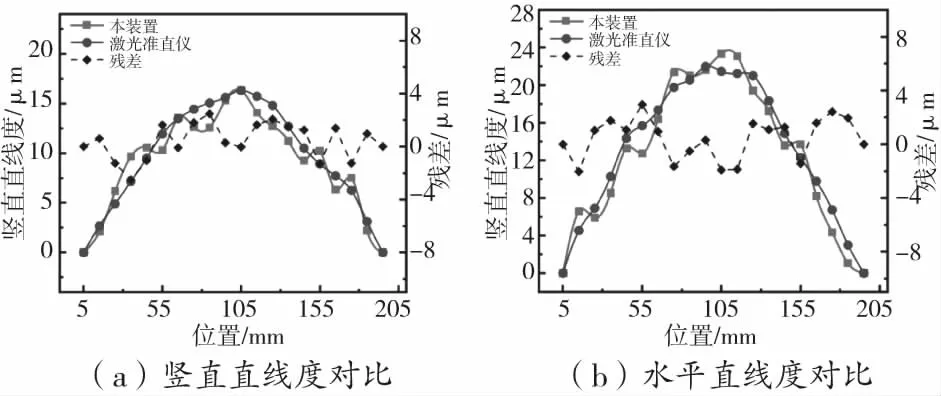
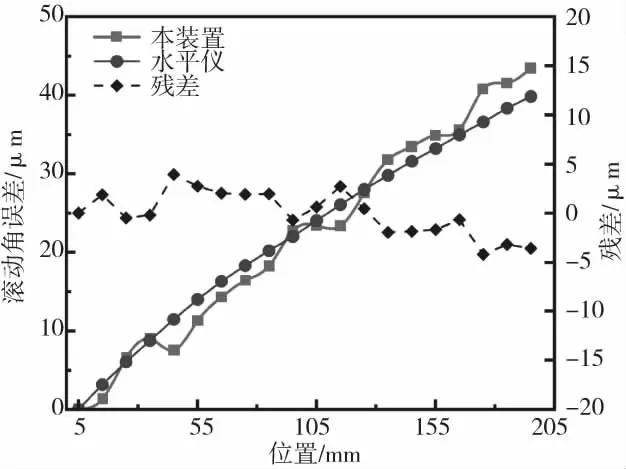
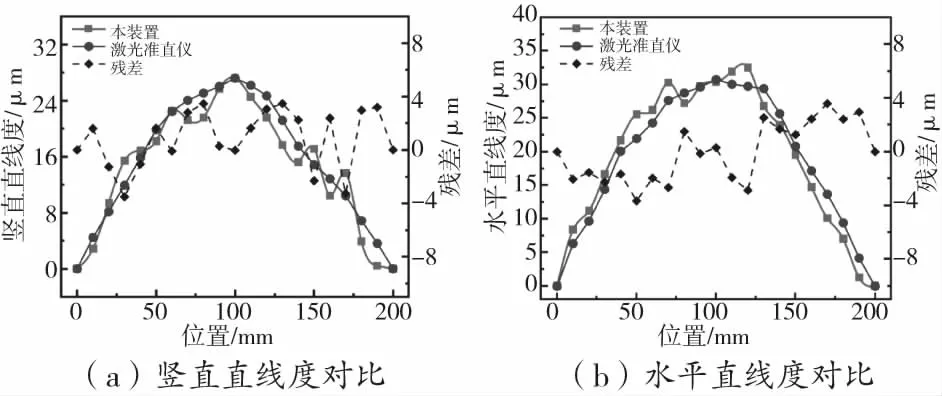
测量行程为200 mm,间隔为10 mm,每个面测量5次,最终结果取平均值。采用三弯矩算法的三次样条插值法对21个测量点进行插值,实现测量范围内对任意点进行补偿。原理如下:设区间[a,b]给出n个插值节点a=x1 2.2.1 直线度对比实验 直线度对比实验使用本装置与激光准直仪同时对直线导轨进行测量。测量时,四象限传感器(QPD)安装位置尽量贴合探头,以减小阿贝臂,避免测量过程中因为角度误差产生阿贝误差,影响比对结果。测量过程如图12所示。 通过1.3章节的分析,误差补偿后的探头位移变化量Δx1(i)与Δx3(i)即为竖直直线度δy与水平直线度δx。为了避开参考面误差的测量点,以验证任意点测量的准确性,在5~195 mm的导轨行程内,以10 mm为步长进行5次测量。取平均值作为测量结果。对比结果如图13所示。本装置与准直仪的最大对比残差约为±2.5 μm和±3.0 μm左右,验证了本系统测量直线度的准确性。 图11 参考面误差测量结果 图12 直线度对比实验 图13 测量结果对比 2.2.2 滚动角对比实验 图14 滚动角对比实验 图15 基准安装平行度误差 通过电子水平仪(青岛前哨WL/AL11,分辨率0.2″)与探头共同对导轨滚动角进行测量,并利用公式(6)求解基准安装平行度误差。如图14所示,水平仪固定到运动平台上。分别在直线导轨的10 mm、50 mm、90 mm、130 mm和170 mm处测量,得到探头测量的滚动角数值与水平仪测量的滚动角数值,两者的差值即为基准安装平行度误差εθ。测量结果如图15所示,εθ平均值为19.4″,标准差为2.4″。 图16 角度测量对比 滚动角对比实验是将本装置与电子水平仪同时固定在运动平台上进行测量,如图14所示。测量范围5~195 mm,测量点间距为10 mm,进行5次滚动角误差测量,最终取平均值作为测量结果。根据公式(7)可以算出滚动角,其中L=230 mm。角度值由本装置和水平仪同时读出,结果如图16所示,可知本装置与水平仪的最大对比残差为±4.2″。 2.2.3 动态对比实验 在实际测量中,待测导轨通常承受时变外力,其几何运动误差常常会发生变化,比如机床线性运动轴。为了模拟测量系统在实际工况下的测量准确性,在下面的测量实验中,平台上放置了重物块,以改变导轨的直线度误差和滚动角误差,模拟施加外力的情况。使用本装置与准直仪、水平仪同时进行直线度与角度的测量实验。测量范围为0~200 mm,测量间距为10 mm。对比结果如图17、图18所示。根据测量结果,竖直直线度对比残差在±3.5 μm,水平直线度对比残差在±3.7 μm,滚动角对比残差在±5″。这说明在受外力的情况下,本装置与标准仪器的测量精度相差不大,进一步验证了该系统进行在机测量的可行性与有效性。 图17 受力情况下直线度测量对比 图18 受力状态下滚动角测量对比 本文针对在机测量的难点,导轨误差离线测量与实际工况测量结果不一致的情况,提出了一种基于电涡流传感器的机床导轨运动误差在机测量方法。电涡流位移传感器的分辨率高、抗干扰强等优点保证了系统的实时性和稳定性。并且建立了直线度、角度计算模型,对参考基准平面度误差以及参考基准安装误差进行了补偿,保证了测量系统的精度。静态与动态对比实验表明,提出的测量系统对直线度的测量精度为:±3.7 μm,滚动角的测量精度约为±5″,验证了该方法的有效性。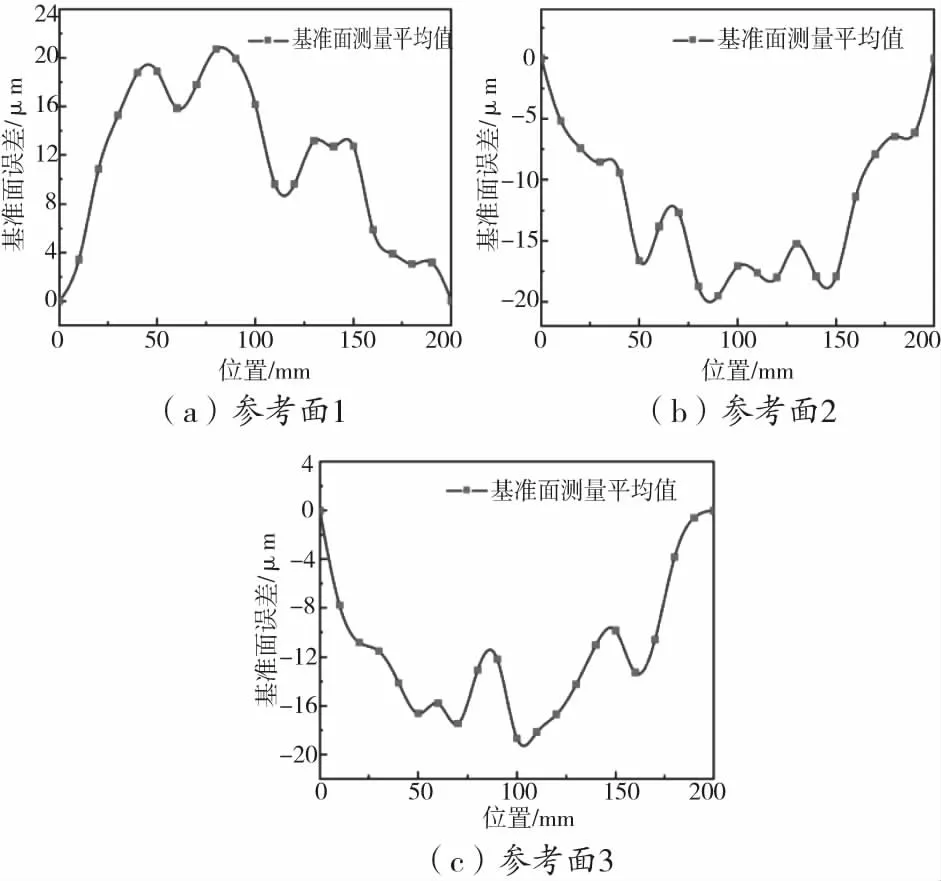


3 结论

