基于预应力监测的锚固边坡整体稳定性分析
嵇其伟, 史克友, 洪英维
(1.江西省交通设计研究院有限责任公司, 南昌 330001; 2.河南工业大学土木工程学院, 郑州 450001; 3.中铁上海设计院集团有限公司, 上海 200070)
高速公路、铁路的修建,很多工程都是在山区进行,难免会出现高挖深填的现象,从而造成了大量人工边坡和次生边坡,如何保证这些人工边坡和次生边坡的稳定性是工程顺利进行、道路安全运营的前提[1-3]。边坡的支护方法有很多种,常用的边坡支护结构有挡土墙[4]、抗滑桩[5],预应力锚杆[6]和预应力锚索[7],其中预应力锚索凭借其强度可靠、施工简便及经济实惠等优点在边坡支护工程中得到了广泛的应用[8-9]。预应力锚索可以充分发挥自身的强度,将岩体软弱结构面与稳定岩层联系在一起,从而改变边坡岩体原有的应力状态,提高边坡的整体稳定性。
预应力锚索的有效预应力是锚索加固边坡稳定性的重要因素,但是由于受施工扰动、开挖卸荷等因素的影响,锚索张拉完成后其预应力都会出现不同程度的损失[10-12], 在对锚索加固边坡进行稳定性分析时,不应忽视锚索预应力损失所造成的影响,尤其是对多锚索加固边坡而言,作用于边坡不同位置处的锚索对边坡的加固效果也不相同。在岩土工程中,极限分析上限法被广泛应用于边坡的稳定性分析中[13-14],许多学者研究指出极限分析上限法同样适用于锚杆或锚索加固边坡的稳定性分析[15]。采用极限分析上限法对预应力锚索加固边坡进行稳定性分析时,通常是将锚索的有效预应力简化成作用于滑动坡体底部的集中力,将锚索的加固效果转化坡体滑动时集中力所做功率进行能耗计算[16-18],这种计算方法已被证实具有精确性及有效性。但是采用这种方法分析锚索加固边坡的稳定性时,人们大多采用锚索的设计张拉值进行计算,忽略了锚索预应力的损失及腐蚀,不仅造成了边坡稳定性计算结果的失真,同时无法对锚索的加固效果进行准确评价。
鉴于此,现对多锚加固边坡锚索的预应力进行现场监测,对比分析位于边坡不同位置处锚索的预应力损失情况及变化规律。并根据锚索的实测预应力值,基于改进的最小耗能原理的塑性极限分析上限法,将各个监测时间点下锚索的实测预应力值代入公式进行了计算,以此对锚索加固边坡的局部动态进行了分析,探讨作用于边坡不同位置处锚索的加固效果,为锚索加固边坡的施工及锚索预应力补强措施提供一些参考。
1 工程概况与监测方法
1.1 工程概况
郑西高速EK1+560~EK1+711段位于洛阳市庙子镇内,该地段处于洪洛河峡谷区,地势险要,地形起伏大,存在大量深挖路堑段。该路堑段地层上伏第四系残坡积,厚度较小,下层岩土体分为强风化石英片岩和中风化石英片岩2个工程地质层,边坡开挖深度范围内主要以强风化石英片岩为主,岩层参数如表1所示。该深路堑段地下水主要为第四系松散岩类裂隙水及基岩裂隙水,补给来源为大气降水及地表河水渗入补给,勘察期间未见地下水位。
现场试验以EK1+640断面为研究对象,该断面路堑边坡高70.6 m,分7级进行开挖,现场采用边开挖边支护的方式进行施工。第一级边坡采用窗孔式护面墙进行支护;第2、3、6级边坡采用框格梁加预应力锚杆进行支护,每根锚杆长9 m,锚杆设计张拉值为90 kN/m;第4、5级边坡采用框格梁加预应力锚索进行支护(图1),锚索长22 m,锚固段长10 m,锚索间垂直间距为2 m,锚索与水平方向的夹角为20°,锚索设计张拉值为400 kN/m。锚孔直径为130 mm,注浆采用M40水泥砂浆。每根锚索由四根钢绞线组成,所采用钢绞线的直径为15 mm,公称面积为140 mm2,抗拉强度为1 860 MPa,弹性模量为1.95×105MPa。框格梁采用C25混凝土进行浇筑,框格梁的截面尺寸为0.4 m×0.4 m,弹性模量为2.8×104MPa。
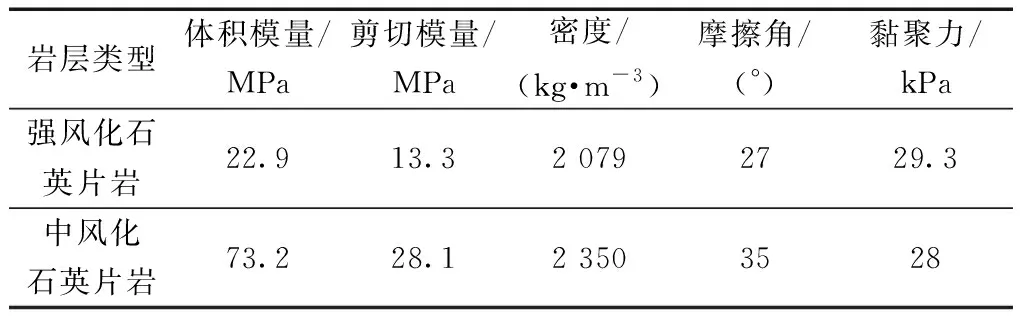
表1 岩层参数Table 1 Rock mass parameters
1.2 监测方案
根据图1的监测方案,锚索张拉前在第4、5级边坡每根锚索的锚具下安装一个预应力传感器(图2),4级边坡所安装的预应力传感器编号由下至上依次为C1、C2、C3、C4,5级边坡所安装的预应力传感器编号由下至上依次为C5、C6、C7、C8。传感器采用JMZX-3108HAT型智能弦式数码穿心力传感器,所用传感器量程为800 kN,灵敏度为0.1 kN。监测数据采集方法如下:①现场安装DSC无线数据采集系统(图3);②利用GPRS的互联网功能,通过约定域名的方式,建立现场上网手机模块;③用安装专业软件的电脑通过无线网络接收数据;④锚索预应力监测开始前,首先对电脑接收软件进行设置,将数据监测设置成自动监测的模式。设置完成后,数据采集设备每天6:00自动采集并报保存数据。
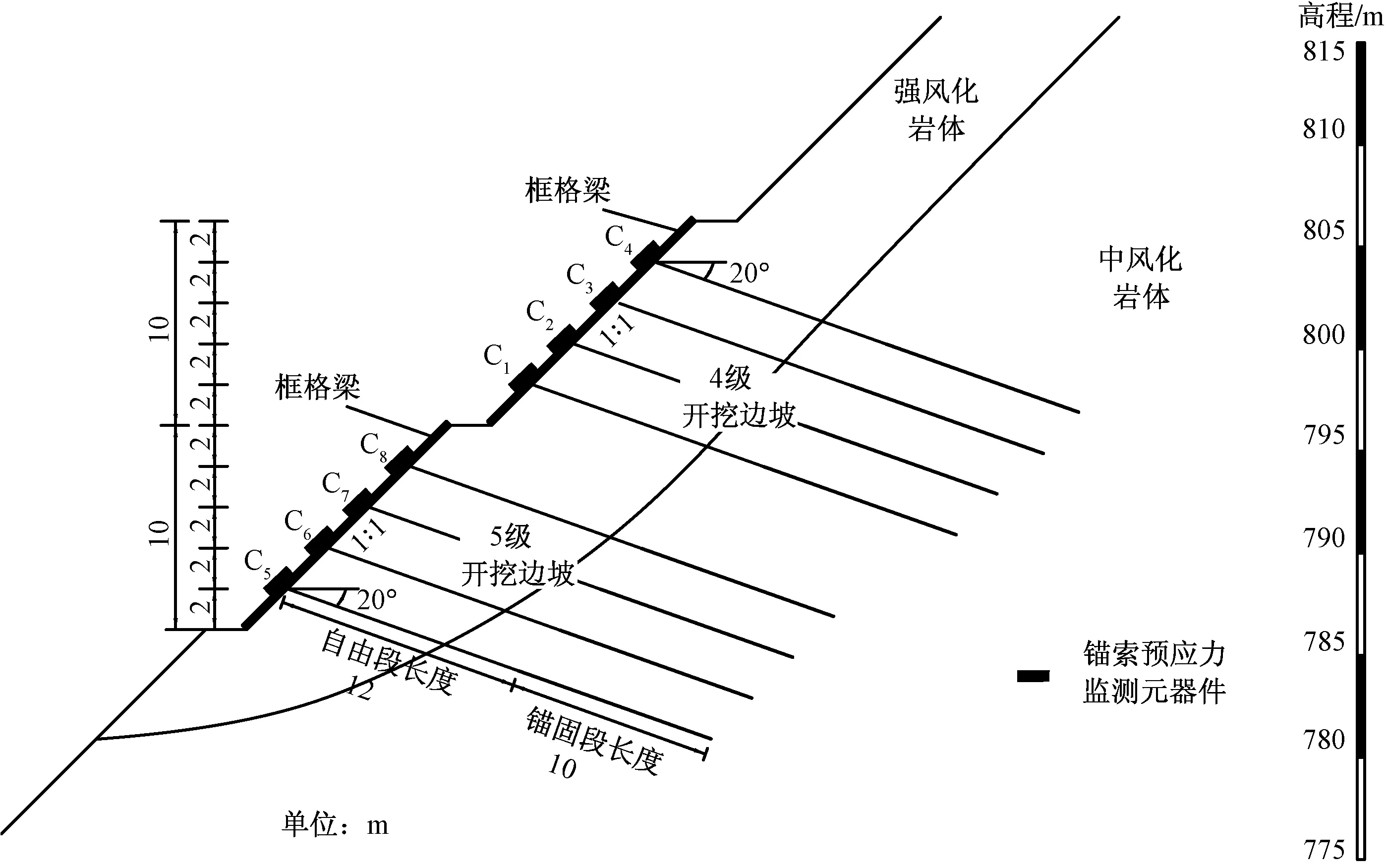
图1 深路堑边坡支护及监测方案Fig.1 Support and monitoring scheme of deep cutting slope

图2 传感器安装Fig.2 Sensor installation

图3 数据采集系统安装Fig.3 Data acquisition system installation
2 监测结果分析
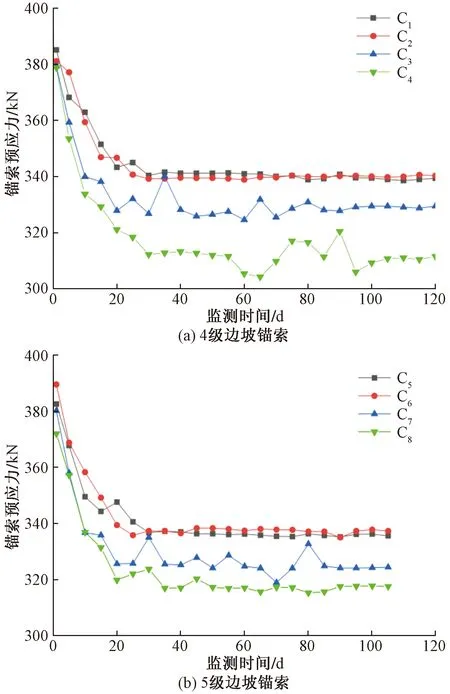
图4 锚索预应力监测曲线Fig.4 Monitoring curves of prestress of anchor cables
传感器安装与现场锚索张拉施工同时进行,监测时间由锚索张拉完成后第2天开始。图4为各锚索预应力的监测曲线。从图4可以看到,锚索张拉完成后所有锚索的预应力均会出现不同程度的损失,这和锚杆的内力变化规律不同,由于锚杆的轴力变化主要是和边坡的侧向变形有关,锚杆在发挥作用期间会有一定程度的轴力增长,而锚索设计长度较长(以此次监测锚索为例,长度为22 m),直接和路堑边坡深部岩体紧密联系在一起,深层风化岩体裂隙的压缩变形大于单级边坡的侧向变形,从而使得锚索的预应力出现不同程度的损失。
锚索预应力的变化规律大致可以分为快速损失、波动变化及稳定变化3个阶段。快速损失阶段发生于锚索作用初期,在此阶段锚索预应力损失主要受锚具变形、钢绞线的收缩、风化岩体裂隙受压致密的影响,该阶段持续时间较短,为20~25 d,但锚索预应力的损失率最大,以第4级边坡为例[图4(a)],在快速损失阶段,锚索C1的预应力由开始监测时的384.1 kN,损失至约351 kN,损失率约为8.49%,锚索C2、C3、C4的损失率分别约为10.15%、9.83%、15.52%,快速损失阶段锚索预应力的损失率占总损失率的70%~90%。波动变化阶段发生于锚索作用中期,在此阶段岩体裂隙已近乎密合,锚索预应力损失主要受施工扰动和环境变化的影响。稳定变化阶段发生于锚索作用后期,此时锚索预应力变化已趋于稳定,预应力损失率很小,该锚索预应力的损失主要与岩体的蠕变变形有关。通过对锚索预应力3个损失阶段的分析可知,快速损失阶段锚索预应力的损失率最大,且在快速损失阶段后岩体整体性有所提高,此时进行锚索的二次张拉可达到更好的预应力补偿效果。
进一步分析可知,锚索C3预应力的最大波动幅值约为13.3 kN,相对于稳定值333.5 kN而言,锚索C3的预应力值的最大波动范围约为4%,锚索C4、C7、C8预应力值的最大波动范围分别约为2.9%、2.8%及2.1%。相比之下,虽然锚索C1、C2、C5、C6的预应力值也并非一成不变,但相对于它们的稳定值而言,由于其预应力值变化范围不大,可认为它们的预应力值没有出现明显的波动现象。
为分析不同位置处锚索的预应力损失率,表2对第4、5级边坡锚索的预应力损失情况进行了对比。如表2所示,每级边坡各锚索的总损失率不尽相同,4级边坡各锚索中锚索C4的总损失率最大,约为17.7%,5级边坡各锚索中锚索C8的总损失率最大,约为14.6%,结合图1中各个锚索的作用位置可以知道,预应力损失程度较大的锚索集中作用于每级边坡的坡顶处。这主要是因为在张拉完成后,锚索处于反向受荷的状态,锚索作用范围内岩体的滑移趋势越强,其受荷越大,其预应力损失量越小。对于每级边坡而言,在上覆荷载(外部荷载及上级边坡等效荷载)作用下,坡顶处边坡的滑移趋势最小,因此此处锚索的预应力损失率也最大。另外还可以看到,作用于每级边坡坡顶处的锚索其预应力还有明显的波动变化现象,说明这些作用位置处的锚索受环境变化和施工扰动的影响也比较大。
可见,对于多锚索加固边坡而言,不同位置处的锚索其预应力的变化情况相差很大,这样很容易造成框格梁的受力不均,从而使得框格梁产生较大的拉应力,进而造成混凝土的开裂,因此施工中应尽量提高施工工艺、提高锚具安装处框格梁的平整度及张拉工艺,尽量减小多锚索加固边坡预应力的不均衡损失。
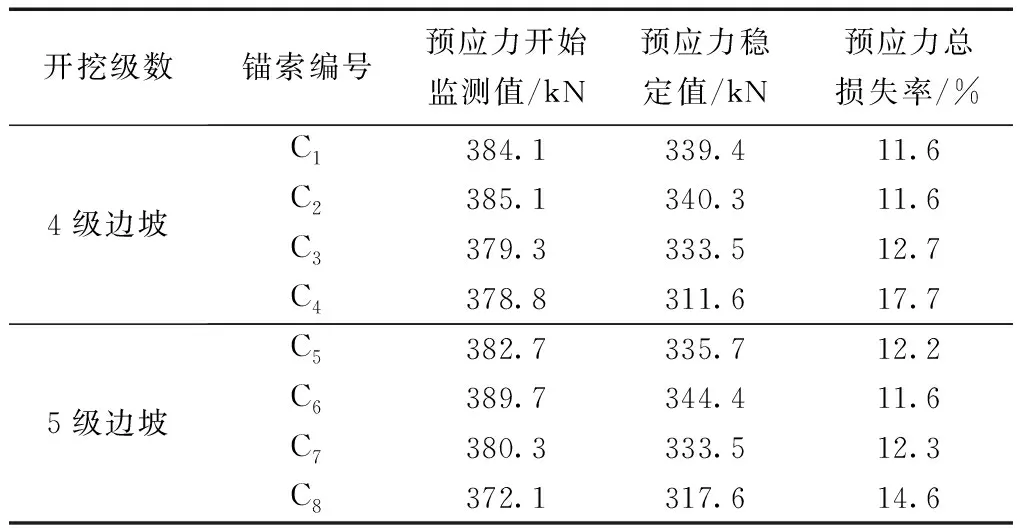
表2 锚索预应力监测结果Table 2 Monitoring results of prestress of anchor cables
3 多锚边坡整体稳定性分析方法
基于最小耗能原理的塑性极限分析上限法在边坡稳定性分析中得到了广泛应用。邓东平等[15]、赵炼恒等[18]通过研究指出此种方法也同样适用于锚固边坡的稳定性分析。采用上限法分析边坡的稳定性时,首先做如下假设:①假设边坡足够长,以平面应变问题对边坡进行稳定性分析;②岩土体的破坏服从摩尔-库伦破坏准则及相关流动准则;③强度折减时只对岩土体的抗剪强度指标进行折减。为便于在实际工程中的应用,本文研究在已有研究理论的基础上,在进行边坡稳定性分析时增加考虑了顶部等效集中荷载的作用。
3.1 多锚边坡失稳机制
已有研究[18]表明,均质边坡的最危险滑动面和对数螺旋面十分接近,因此在对均质边坡进行稳定性分析时,可将均质边坡的假想破裂面简化为如图5所示的形状。根据前文中的假设,可认为滑动区域DABCD以O点为旋转中心相对于曲面AD以下静止区域作刚体旋转。
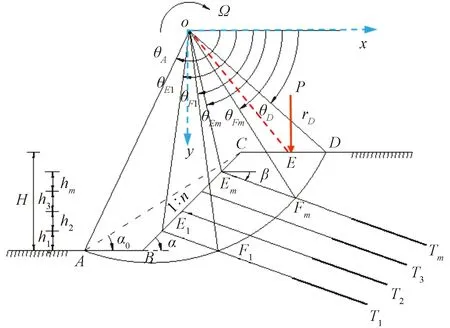
θA为极坐标中滑裂面底脚A点对应的角度;θD为极坐标 中滑裂面顶脚D点对应的角度;α0为边坡顶脚C点和滑裂 面底脚A点的连线与水平面的夹角;假想破裂面由变量θA、θD、α0 确定;Ω为滑块区域DABCD的转动角速度;rD为OD段长度; θE1、θEm为极坐标中E1、Em点对应的角度;θF1、θFm为极坐标 中F1、Fm点对应的角度;α为边坡坡角;β为锚索与水平面的夹角; H为边坡高度;h1~hm为各锚索锚固点至坡脚的垂直距离图5 多锚边坡破坏机制Fig.5 Failure mechanism of multi-anchor reinforced slope
3.2 多锚边坡能耗计算
在岩土体自重条件下,由图5所示锚索加固边坡稳定性分析的破坏机制可知,对锚固边坡进行上限分析时的能耗计算包括4个方面的内容:滑动区域DABCD在重力下做功、滑动面内能耗散做功、等效集中荷载P做功及锚索预应力做功。
(1)滑动区域重力做功。假设滑动区域DABCD在重力下所做功率为Ws,区域OAD、OCD、OCA、CAB在重力下所做功率分别为W1、W2、W3、W4,则Ws=W1-W2-W3-W4即为滑动区域DABCD在重力下所做的功率:
Ws=W1-W2-W3-W4
(1)
式(1)中:γ为岩土体重度;函数f1、f2、f3、f4为与θA、θD等参数相关的函数,其具体表达式见文献[19]。
(2)滑动面内能耗散做功。滑动面内能耗散发生在滑动面AD上,滑动面AD内能耗散率的微分可以由该面的微分面积dθ/cosφ与岩土体黏聚力c以及该面的切向线速度Vcosφ的乘积得到,沿整个滑动面积分,即得到滑动面总的内部能量耗散率为
(2)
式(2)中:c为岩土体黏聚力;φ为岩土体内摩擦角。
(3)锚索预应力做功。由图6所示破坏机制中的几何关系可知,当锚索1的预应力T1作用点位置位于E1点时,预应力T1所做的外力功为

(3)
当锚索1的预应力T1作用点位置位于F1点时,预应力T1所做的外力功为

(4)
式(4)中:WT1为预应力T1所做的外力功;T1为锚索1的预应力;vE1为极坐标中E1点对应的线速度;vF1为极坐标中F1点对应的线速度。
由已有研究可知,锚索1的预应力T1作用于点E1和点F1时计算所得的功率是相同的。本文研究中选取预应力T1作用于E1点时进行计算,根据图5所示几何关系可知,在极坐标中:
(5)
(6)
(7)
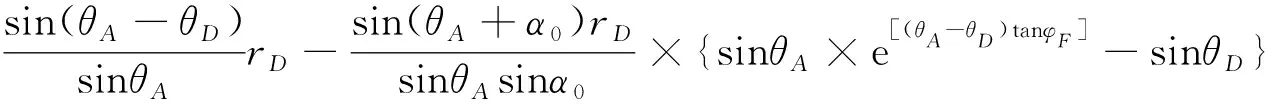
(8)
与上述方法一样,可以求出预应力T2、T3、T4所做的外力功分别为
(9)
(10)
(11)
(4)等效集中荷载做功。如图5所示,假设等效集中荷载P作用于E点,E点在极坐标中对应的角度为θE,E点距边坡顶点C的长度为LCE,由图5中几何关系可知:
(12)
(13)
则O点到等效集中荷载作用点E点的长度为
(14)
可以求得等效集中荷载P所做的外力功为
WP=PvEcosθE=PLOEΩcosθE
(15)
3.3 多锚边坡稳定性计算
基于上限法基于最小耗能原理,使外荷载所做功率等于滑动面内能耗散功率,同时结合强度折减理论,将岩土体的抗剪强度指标c和φ替换成折减后的cF、φF,即可求得临界高度时,在锚索预应力作用下锚固边坡的安全稳定性系数。
当LCE>LCD时,做功外荷载为滑体自重荷载及锚索锚固荷载,此时临界高度时锚固边坡的稳定性系数为
(16)
(17)
式中:系数f1、f2、f3、f4中的岩土体内摩擦角φ同样替换成折减后的内摩擦角φF。
当LCE (18) 式(18)中:锚索预应力作用下锚固边坡的安全稳定性系数FS变量θA、θD、α0的函数,FS取得极值时,变量θA、θD、α0应满足以下约束条件: (19) 以式(19)为约束条件对式(18)进行计算,即可求得锚索预应力作用下锚固边坡的安全稳定性系数FS。由于式(18)是一个包含安全稳定性系数FS的隐函数,因此,可以采用迭代优化算法对其进行计算 为研究锚索预应力损失及锚索作用位置对多锚边坡整体稳定性的影响,这里以第4级边坡为例对此进行分析,根据表1岩体的计算参数并结合锚索实测预应力值及上文中分析的锚固边坡的稳定性分析方法,可以求得第4级边坡各锚索预应力快速损失后(以第20天的监测数据为例)边坡的实际稳定系数。表3为锚索预应力损失对边坡整体稳定性的影响计算结果。由计算结果可知,没有进行锚索加固时,边坡的稳定性计算结果为1.372。对边坡进行多锚索加固后,按设计锚固荷载进行计算时,边坡的稳定性计算结果为1.98;当各锚索预应力快速损失后,边坡的稳定性计算结果为1.874。可见,对边坡进行预应力锚索加固后可以显著提高边坡的整体稳定性,但如果忽略锚索预应力的损失,以设计锚固荷载对边坡进行稳定性计算,会造成计算结果的偏大。 表3 锚索预应力损失对边坡整体稳定性的影响Table 3 Influence of prestress loss of anchor cables on overall stability of slope 通过前面对锚索预应力的监测结果可知,锚索预应力在经历快速损失阶段后进入波动变化阶段,为研究波动变化阶段多锚边坡的整体稳定性演变规律及锚索作用位置对边坡整体稳定性的影响,表4给出了锚索预应力波动变化时多锚边坡的整体稳定性计算结果。由表4可知,4根锚索预应力同时波动变化时,边坡稳定性计算结果的变化范围为1.874~1.769。其他3根锚索预应力保持不变,仅锚索C3预应力波动变化时,边坡稳定性计算结果的变化范围最大,虽然波动变化阶段锚索C4预应力的变化范围也比较大[图4(a)],但由于锚索C4的作用位置位于该级边坡顶处,坡顶处边坡的滑移趋势最小,其预应力波动对边坡的整体稳定性影响有限,也就是说对于多锚加固边坡而言,边坡中下部各锚索是控制其整体稳定性的关键。因此,在多锚索加固边坡施工完成一段时间后,应对锚索进行二次张拉或采取其他措施补强锚索的有效预应力,尤其是对位于边坡中下部锚索进行预应力补偿,可以显著提高边坡的整体稳定性。 表4 锚索作用位置对边坡整体稳定性的影响Table 4 Influence of anchor cable position on overall stability of slope (1)对多锚边坡的锚索预应力进行了长期监测,监测结果表明快速损失阶段锚索预应力的损失比重最大,占总损失率的70%~90%,预应力损失程度较大的锚索集中作用于每级边坡的坡顶处,此外,该处锚索对环境变化和施工扰动也比较敏感。在锚索预应力波动变化阶段,边坡中上部各锚索预应力的波动范围为2%~4%,虽然边坡中下部各锚索的预应力值也并非一成不变,但相对于它们的稳定值而言,可认为它们的预应力值没有出现明显的波动现象。 (2)基于最小耗能原理的塑性极限分析上限法并结合锚索的实测预应力值对多锚边坡的整体稳定性进行了分析,可见,对边坡进行锚索加固后可以显著提高边坡的整体稳定性,但如果忽略锚索预应力的损失,以设计锚固荷载对边坡进行稳定性计算,会造成计算结果的偏大。 (3)在锚索预应力波动变化阶段,仅锚索C3预应力波动变化时,边坡整体稳定性计算结果的变化范围最大,结合锚索C3的作用位置可知,中下部各锚索是控制边坡整体稳定性的关键。在对锚索预应力的后期补强中,应着重加强边坡中下部各锚索的预应力补偿,以显著提高多锚加固边坡的整体稳定性。4 基于监测结果的多锚边坡整体稳定性分析


5 结论

