用函数的眼光看方程和不等式

文／段侠

教材中的例题、习题都是经过编者精心设计的，是我们学习知识的桥梁、解题方法的示范。因此，对例题、习题进行深挖和进一步探究就显得尤为重要。下面，我们先来看看苏科版数学教材九年级下册第24页的“观察与思考”。

图1

图2

图3

【解析】求一元二次方程ax2+bx+c=0（a≠0）的根，相当于求使二次函数y=ax2+bx+c（a≠0）的函数值为0时x的值，即函数与x轴交点的横坐标的值。本题可将判断方程的根的情况转化为判断二次函数与x轴的交点个数，进而完成求解。由图1可知，函数与x轴有两个交点，则方程两个不相等的实数根；由图2可知，函数y=x2-6x+9与x轴有1个交点，则方程x2-6x+9=0有两个相等的实数根；由图3可知，函数y=x2-2x+3与x轴无交点，则方程x2-2x+3=0无实数根。

延伸探究1根据图1，回答下列问题：

（1）当y＞0时，x的取值范围是___；

（2）当y＜0时，x的取值范围是___；

（3）当y＜-6时，x的取值范围是___；

（4）当-6＜x＜0时，y的取值范围是___。

【解析】本题可将不等式问题转化为函数问题求解。

（1）y＞0相当于函数值为正数，从图1中易得，当-6＜x＜-2时，y＞0；

（2）当x＜-6或x＞-2时，y＜0；

（3）如图4，作直线y=-6，它与函数y=有两个交点（交点的横坐标分别是0和-8），由此可知，当x＜-8或x＞0时，y＜-6；

图4

（4）如图5，分别作直线x=0、x=-6，它们分别与函数交于点（0，-6）、（-6，0），易求得函数的顶点坐标为（-4，2），由此可知当-6＜x＜0时，-6＜y≤2。

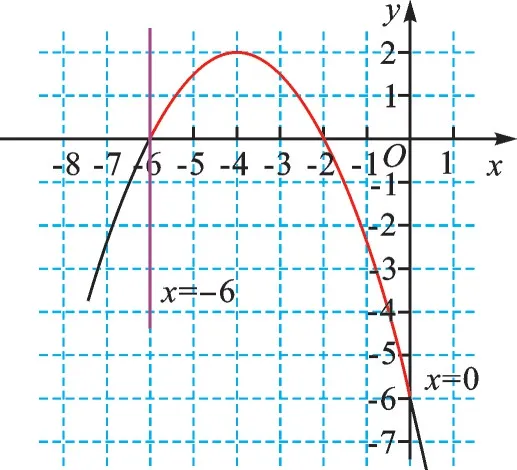
图5

延伸探究2根据图1，讨论方程4x-6=a的解的情况。

【解析】方程的解的情况可转化为求二次函数与直线y=a的交点问题。

（1）当a＞2时，两函数无交点，方程无实数根；

（2）当a=2时，两函数有一个公共点，方程有两个相等的实数根；

（3）当a＜2时，两函数有两个公共点，方程有两个不相等的实数根。

延伸探究3如图6，一次函数y1=x与二次函数y2=ax2+bx+c的图像相交于P、Q两点，则函数y=ax2+（b-1）x+c的图像可能为（ ）。

图6

【解析】由图6可知，一次函数y1=x与二次函数y2=ax2+bx+c图像在第一象限相交于P、Q两点，则一元二次方程ax2+bx+c=x有两个不相等的正根，即关于x的一元二次方程ax2+（b-1）x+c=0有两个不相等的正实数根，则函数y=ax2+（b-1）x+c的图像与x正半轴有两个交点，故A符合题意。

【点评】“转化”和“数形结合”是数学中常用的两种思想方法。我们通过对“思考与观察”的延伸探究，让大家感受二次函数与方程、不等式的关系，巩固和拓宽思维，培养“看图说话”和解决问题的能力。

拓展变式1已知二次函数y=ax2+bx+c（a≠0）中，函数y与自变量x的部分对应值如下表所示：

x y……-1-6 0-1 1 2 2 3 3 2……

则当y＞-1时，x的取值范围是___。

【解析】由表格可知，当x=1和3时，y的值都为2，则二次函数的对称轴为直线x=2；而当x=0时，y=-1，根据二次函数的对称性知，当x=4时，y=-1。又因为当x＜2时，y随x的增大而增大，所以二次函数的开口向下，所以当0＜x＜4时，y＞-1。

拓展变式2已知二次函数y=x2-4mx+3m2（m≠0）。

（1）求证：该二次函数的图像与x轴总有两个公共点；

（2）设该二次函数与x轴的两个交点分别为A、B，若m＞0，且A、B两点间的距离为2，求m的值并直接写出y＞3时，x的取值范围。

【解析】（1）证明：令y=0，则x2-4mx+3m2=0（m≠0）。

∵b2-4ac=（-4m）2-4×1×3m2=4m2＞0，

∴方程x2-4mx+3m2=0有两个不相等的实数根。

∴该二次函数图像与x轴总有两个公共点。

（2）解：∵y=x2-4mx+3m2=（x-m）（x-3m），

∴A（m，0），B（3m，0）。

∵两交点间距离为2，且m＞0，

∴3m-m=2。

∴m=1，即m的值为1。

当m=1时，y=x2-4x+3。

把y=3代入y=x2-4x+3，

得3=x2-4x+3，解得x=0或x=4。

∵抛物线开口向上，

∴当y＞3时，x的取值范围是x＜0或x＞4。

【点评】这两道“拓展变式”虽然和前面三道“延伸探究”在形式上不同，但本质上依旧考查函数与方程、不等式的关系。我们在解答这类题时，既要学会识图，还要清楚函数图像背后的本质，以不变应万变，会一题通一类，方可做到对知识的懂、透、化。