化难为易过“三关”

文／曹小龙

二次函数内容丰富，难点颇多，综合性强，令很多同学望而却步。本文列举三个方面简述突破之法。

一、图像与性质

例1在平面直角坐标系中，已知二次函数y=ax2+bx+c（a≠0）的图像如图1所示，有下列5个结论：①abc＞0；②2a-b=0；③9a+3b+c＞0；④b2＞4ac；⑤a+c＜b。其中正确的有（ ）。

图1

A.1个 B.2个 C.3个 D.4个

【分析】由抛物线开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据抛物线对称性推理判断。

解：∵图像开口向下，∴a＜0。

∵对称轴为直线

∴b=-2a＞0。

∵图像与y轴的交点在x轴的上方，

∴c＞0。∴abc＜0，①错误。

∴2a-b=-2b＜0，所以②错误。

由图像可知点（-1，0）关于x=1的对称点为（3，0）。

∵当x=-1时，y＜0，

∴当x=3时，y＜0。

∴9a+3b+c＜0，③错误。

∵抛物线与x轴有两个交点，

∴b2-4ac＞0。∴b2＞4ac，④正确。

当x=-1时，y＜0，

∴a-b+c＜0。∴a+c＜b，⑤正确。

∴正确的为④⑤，故选B。

二、模型与应用

例2某商品有线上、线下两种销售方式。

线上销售：单件利润定为600元时，销售量为0件，单件利润每减少1元销售量增加1件。另需支付其他成本5000元。

线下销售：单件利润500元。另需支付其他成本12500元。

注：净利润=销售商品的利润-其他成本。

（1）线上销售100件的净利润为___元；线下销售100件的净利润为___元；

（2）若销售量为x件，当0＜x≤600时，比较两种销售方式的净利润；

（3）现有该商品400件，若线上、线下同时销售，售完后的最大净利润是多少元？此时线上、线下各销售多少件？

【分析】第（2）问，先分别求出两种销售方式的净利润的函数表达式，再分三种情况讨论，可解方程、不等式；也可作差后根据图像观察求解。第（3）问，需建立关联两种销售方式的新函数表达式，再求最值。

解：（1）45000，37500。

（2）设销售量为x件时，线上销售的净利润为y1元，线下销售的净利润为y2元，线上线下销售的净利润差为w元。则

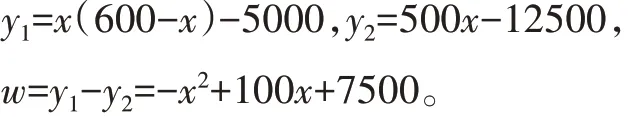
结合二次函数w=-x2+100x+7500的图像可知：

当0＜x＜150时，w＞0，即线上销售的净利润大于线下销售的净利润；

当x=150时，w=0，即线上销售的净利润等于线下销售的净利润；

当150＜x≤600时，w＜0，即线上销售的净利润小于线下销售的净利润。

（3）设线上销售a件时，售完400件商品的净利润为m元。则

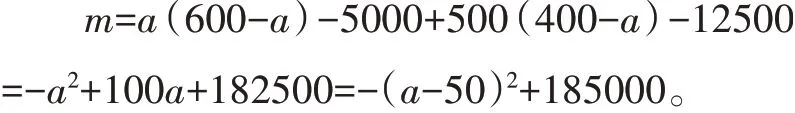
∵m的函数图像是抛物线且开口向下，∴当a=50时，m有最大值185000，即当线上销售50件，线下销售350件时，最大净利润为185000元。

三、含参与综合

例3已知函数y1=x+1和y2=x2+3x+c（c为常数）。

（1）若两个函数图像只有一个公共点，求c的值；

（2）点A在函数y1的图像上，点B在函数y2的图像上，A、B两点的横坐标都为m。若A、B两点的距离为3，直接写出满足条件的m值的个数及其对应的c的取值范围。

【分析】（1）联立方程，通过判别式Δ=0求解。（2）方法一：分别令y1-y2=3，y1-y2=-3，根据关于m的一元二次方程中Δ的取值范围与c的关系列方程或不等式求解。方法二：由（1）结合图像的平移，寻找临界位置，数形结合定范围。

解：（1）两个函数图像只有一个公共点，则方程x2+3x+c=x+1有两个相等的实数根，∴Δ=0，即22-4（c-1）=0。∴c=2。

（2）如图2，当c＞5时，0个；当c=5时，1个；当-1＜c＜5时，2个；当c=-1时，3个；当c＜-1时，4个。

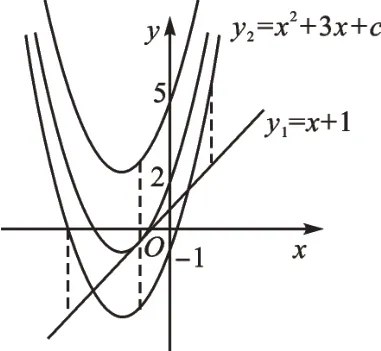
图2

二次函数含参问题中，我们要思考图像的对称轴、与x轴交点及经过的定点能否求出，多画几个草图分析临界位置（如顶点在x轴上时，经过特殊点——原点、定点或其他已知点），观察图像变化，确定参数的取值范围。如a决定形状、开口大小，a的绝对值越大（小），开口就越小（大）等。