温故知新巧用转化妙解最值

文／陈俊

二次函数作为初中数学的重点和难点，一直是中考命题的热点。其中，动点与最值问题，又是同学们感到比较棘手的一类问题。我们可以通过联系以往所学的知识，将陌生问题转化为熟悉问题，将复杂问题转化为简单问题，迅速找到解题的切入点。

一、利用“将军饮马”解决线段最值问题

例1如图1，抛物线y=-x2-2x+3与x轴交于A、B两点，与y轴交于点C，点M在抛物线的对称轴上，当点M到点B的距离与到点C的距离之和最小时，点M的坐标为 。

图1

【分析】点B与点A关于抛物线的对称轴对称，利用“将军饮马”模型，可以将点M到点B的距离与到点C的距离之和，转化为点M到点A的距离与到点C的距离之和。

解：∵抛物线y=-x2-2x+3与x轴交于A、B两点，

∴令y=0，得-x2-2x+3=0，

解得x=-3或x=1。

∴A（-3，0），B（-1，0）。

令x=0，得y=3，

∴C（0，3）。

设直线AC的表达式为y=kx+b，把A（-3，0）、C（0，3）分别代入直线y=kx+b，

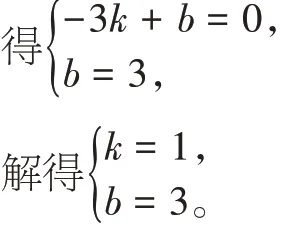
∴直线AC的表达式为y=x+3。

设直线AC与直线x=-1的交点为M，则此时MB+MC的值最小。

把x=-1代入直线y=x+3，得y=2，

∴M（-1，2）。

即当点M到点B的距离与到点C的距离之和最小时，点M的坐标为（-1，2）。

【小结】求两条线段之和最小值的问题，常采用“将军饮马”模型。对于这类问题，首先将动点所在直线看作“河”，再通过找对称点，求出直线表达式，便可解决问题。

二、利用“三点共线”解决线段最值问题

例2如图2，已知直线与y轴交于点A，与x轴交于点D，抛物线与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）。在抛物线的对称轴上找一点M，使 |AM-MC|的值最大，点M的坐标为 。

图2

【分析】由于点C和点B关于抛物线的对称轴对称，那么要求 |AM-MC|最大，即求|AM-MB|最大。根据三角形两边之差小于第三边，故当A、B、M在同一直线上时，|AM-MB|的值最大。

解：由直线可 得 点A坐 标为（0，1）。

将A（0，1）、B（1，0）坐标代入

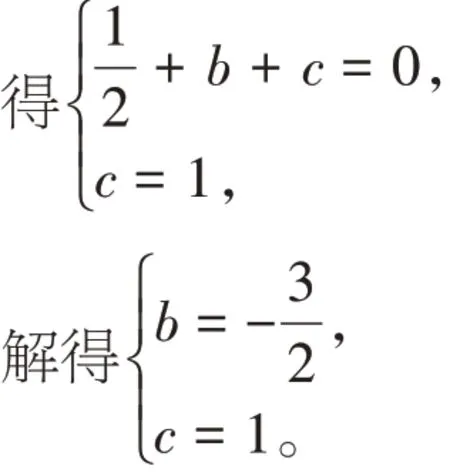
∴抛物线的表达式为

∴抛物线的对称轴为直线∵B、C关于直线对称，

∴MC=MB。

要求 |AM-MC|的最大值，即求|AM-MB|的最大值。

根据三角形两边之差小于第三边，故当A、B、M在同一直线上时，|AM-MB|的值最大。

由A（0，1）、B（1，0）坐标可求出直线AB的表达式为y=-x+1。

∴点M坐标为

【小结】我们对比发现，例1是“三点共线”中求线段和的问题，求的是最小值；例2是“三点共线”中求线段差的问题，求的是最大值。

三、利用“图形分割”和“坐标相减”解决面积最值问题

例3如图3，已知抛物线y=-x2+2x+3与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C（0，3）。点D是第一象限内抛物线上的一个动点（与点C、B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连接BD、CD。设点D的横坐标为m，△BCD的面积为S。求S关于m的函数表达式及自变量m的取值范围，并求出S的最大值。

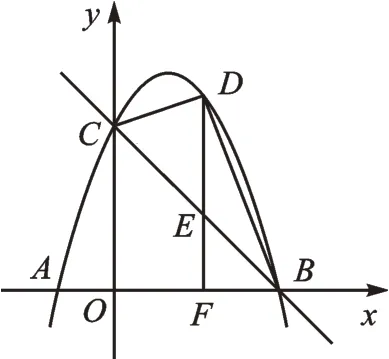
图3

【分析】本题直接表达出△BCD的面积有一定的困难，但我们如果通过图形分割，分别求出△ECD和△EBD的面积，就可以表示出△BCD的面积。本题的另一个难点是动点D的运动使得线段DE的长度发生改变，只要能求出DE的最大值，就能求出S的最大值。

解：设直线BC的表达式为y=kx+b（k≠0）。

∵直线BC过点B（3，0）、C（0，3），

∴y=-x+3。

设点D的坐标为（m，-m2+2m+3），

则点E的坐标为（m，-m+3），

∴当时，S有最大值

【小结】二次函数图像上点的位置的“直观变化”与二次函数表达式确定的“数量变化”之间有着密切的联系。在研究二次函数问题时，我们始终要以“变化与对应”为基础，感受数形关系。