“齐次式”在求解圆锥曲线问题中的妙用

江苏省太仓高级中学 (215400)

方明生

“齐次式”在三角函数及不等式等问题中应用较为广泛，近些年在圆锥曲线模块中出现较为频繁.圆锥曲线问题求解带给学生最大的烦恼就是运算量大，在平时的做题中，不少的学生没有形成正确的学习方法，缺少对题型的归纳整理和思考，通常采用常规的方法进行运算，思路是正确的，但运算能力不足使得运算出错，导致“会而不对”的尴尬局面.本文结合例题，从学生的角度出发，对斜率的和(积)为定值的这类题进行归类，利用“齐次式”法进行巧妙解答，避免繁琐的运算，做到知一题，会一类的效用.

一、斜率之积为定值

例1 (2017年全国Ⅲ卷·理20)已知抛物线C:y2=2x，过点(2,0)的直线l交C于A,B两点，圆M是以线段AB为直径的圆.(1)证明：坐标原点O在圆M上；(2)略.

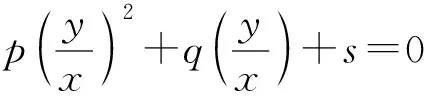
二、斜率之和为定值

(1)求椭圆C的标准方程；

(2)设直线AF,BF的斜率分别为k1,k2(k2≠0)，求证：k1+k2为定值.

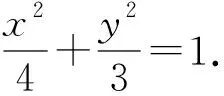
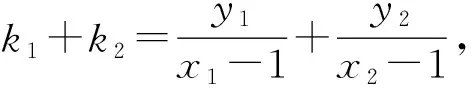
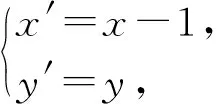
三、直线过定点

(1)求椭圆C的方程；

(2)设A为椭圆C的右顶点，直线l是与椭圆交于M,N两点的任意一条直线，若AM⊥AN，证明直线l过定点.

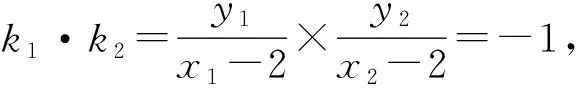
保险柜在书房里，他匆忙把那些东西收起来，锁好，起身正要离开，看到了电脑桌上的红色外套的苹果手机，那是妻子的。看到妻子的手机，他不由得想到了妻子对手机小心谨慎的样子。睡觉时她必需把手机放在自己的枕头底下，同时迅速瞥一眼尹爱群。出门时必要随身携带，从来没有人机分离的情况。这个现象让尹爱群一直感到奇怪，难道妻子的手机里藏着什么隐秘？可是现在，妻子的手机就在自己的手里，可以随意查看，是妻子有意为之还是一时疏忽？

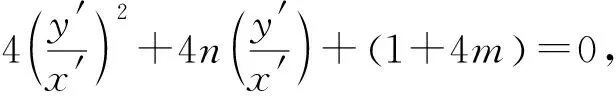
评注：本题已知斜率积为定值，去证明直线恒过定点，此题还可以改编为kAM+kAN=a(a为实数且a≠0),去证明直线过定点，此类题均可通过构造齐次式去求解，但在实际运算中一定要搞清楚直线l与直线l′、圆锥曲线C与C′的区别和联系.

(1)求椭圆C的方程；

(2)经过椭圆右焦点F且斜率为k(k≠0)的动直线l与椭圆交于A、B两点，试问x轴上是否存在异于点F的定点T，使|AF|·|BT|=|BF|·|AT|恒成立？若存在，求出T点坐标，若不存在，说明理由.

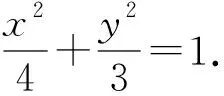
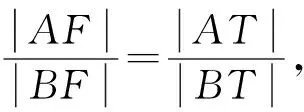
评注：本题第二问难度较大，需要通过|AF|·|BT|=|BF|·|AT|得到面积之比，再通过三角形的面积公式得到两条直线的夹角互补，从而得到斜率之和为0，在运算的时候理清思路，选择恰当的方法可以有效的节省求解时间.

四、斜率的和(积)为定值

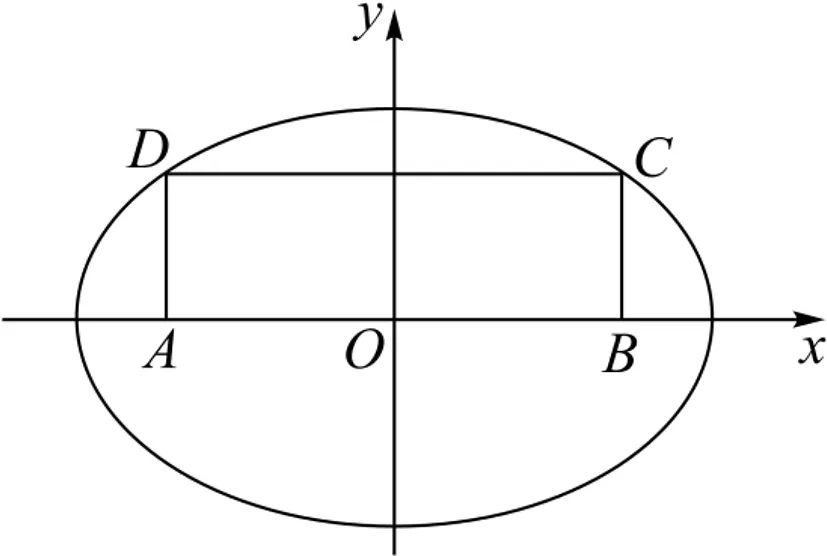
图1

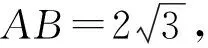
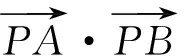
(2)若过点B且斜率为k的直线交椭圆于M、N两点(点C与M、N两点不重合)，且直线CM、CN的斜率分别为k1、k2，试证明k1+k2-2k为定值.

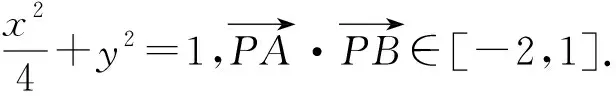
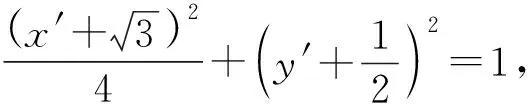
通过以上几个例子我们可以看出，利用齐次式解决斜率的和(积)与直线过定点问题，能够降低运算量，提升运算的准确性.通过对此类题型的分析，总结出以下解题步骤：

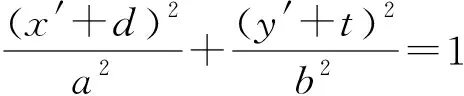
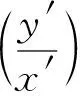
(4)利用韦达定理列出斜率之和(积)的等式；

(5)根据题意求出斜率之积(和)或根据它们是定值求出直线所过定点的坐标.