多变量问题中的“整元、换元、定元”策略*

福建省福清第三中学 (350315)

何文昌

福建省福清三山中学 (350318)

念 杰

不等式、函数与导数问题经常涉及多个变量，这类问题综合性大，技巧性强，学生往往无从下手，给学生的求解带来较大的困难.下面就“含多个变量问题”的“整元、换元、变元”策略作一探析，与同行交流.

一、整元——整合变量

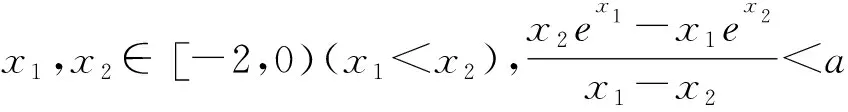
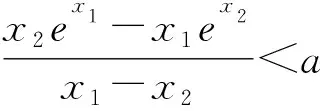
评注：以上问题求解的难点在于它是含三个变量的问题，需要把式子变形转换成同构式，用单调性的定义把同构式转化为双变量问题，再分离参数转化成单变量问题，进而构造函数求解，求解过程用到整元策略.

二、换元——转换变量

(1)若f(x)≥0，求a的取值范围；

(2)证明：若f(x)有两个零点x1,x2，则x1x2<1.

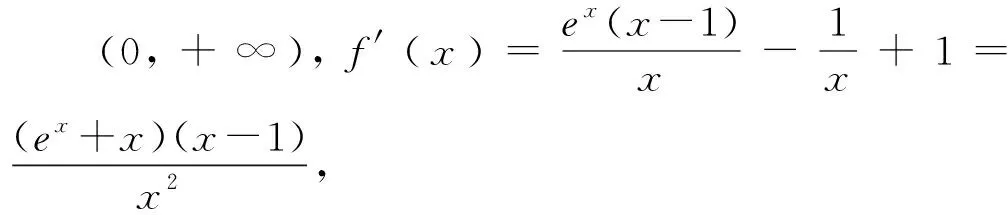
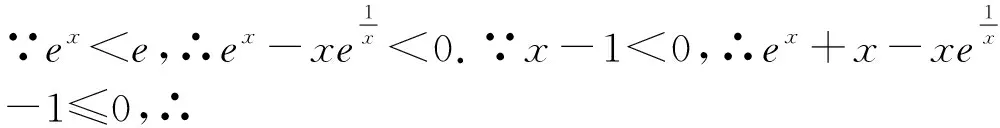
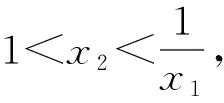
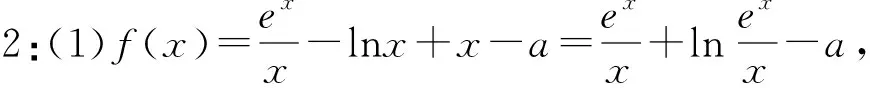
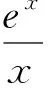
三、定元——确定主次

例3 (2022年北京卷第21题)已知函数f(x)=exln(1+x).

(1)略；(2)设g(x)=f′(x)，讨论g(x)在[0,+∞)上的单调性；

(3)证明：对任意的s,t∈(0,+∞)，有f(s+t)>f(s)+f(t).

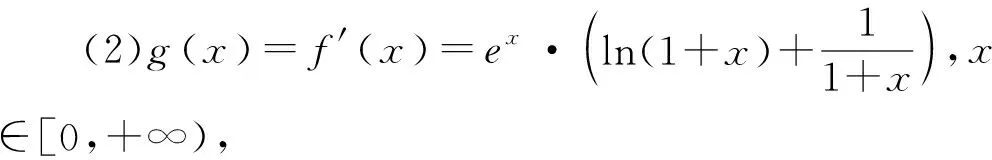
∴g′(x)>0对任意x∈[0,+∞)恒成立，g(x)在[0,+∞)上单调递增.

(3)设m(s)=f(s+t)-f(s)-f(t)，则m′(s)=f′(s+t)-f′(s)=g(s+t)-g(s).由于g(x)在[0,+∞)上单调递增，且s+t>s>0，则g(s+t)>g(s)，因此m′(s)=g(s+t)-g(s)>0，m(s)在(0,+∞)上递增，故m(s)>m(0)=f(0+t)-f(0)-f(t)=-f(0)=0，因此，对任意的s,t∈(0,+∞)，有f(s+t)>f(s)+f(t).

评注：本题第(3)问中f(s+t)>f(s)+f(t)中有双变量，因为s,t彼此独立、地位相同，可以把一个变量确定为主元(自变量)，另一个变量确定为次元(参数)，通过移项、构造函数，把双变量问题转化成单变量问题，再利用导数研究函数的单调性，从而证明结论，证明过程用到定元策略.