“转化·构造·换元”求解一道导数问题

江苏省通州高级中学 (226300)

袁 源

高考数学压轴试题蕴含丰富的数学思想和方法，是研究高考、备战高考的良好素材，笔者对2021年高考数学乙卷理科20题进行解法探究，发现换元法可以快速地求解，于是触发了我的思考.

1.试题呈现及解析

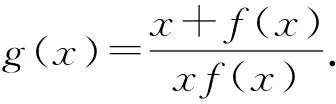
试题设计简洁、解题入口宽，解法灵活多样，能有效地考查函数与导数的基础知识，考查化归与转化思想，突出综合运用所学知识分析问题与解决问题的能力.在解决指数函数不等式、对数函数不等式或指数函数与对数函数混合不等式时，比如在解决恒成立问题或零点问题时，使用参变量分离法、隐零点代换法都避免不了复杂的计算，效果还不一定很好，然而合理使用“转化、构造、换元”三大法宝会达到意想不到的效果.

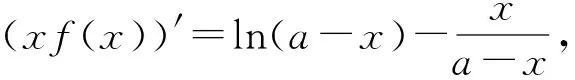
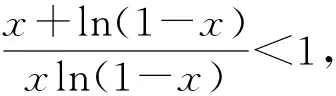
评析：鉴于函数ln(1-x)的形式较为复杂，进行换元，令t=ln(1-x)，再构造函数g(t)=(t-1)et+1,t≠0求解，解法简洁，真正体现了换元思想在导数中的运用魅力.

2.方法应用

例1 已知x3e2x-3lnx-ax-1≥0恒成立，求a的取值范围.

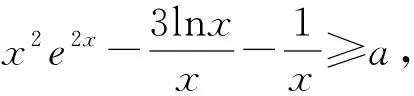
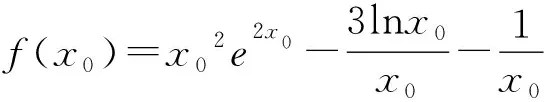
例2 若函数f(x)=(x-2)2ex+ae-x-2a|x-2|有6个零点，求a的取值范围.

解析：因为函数f(x)=(x-2)2ex+ae-x-2a|x-2|有6个零点，所以函数g(x)=(x-2)2e2x-2a|x-2|ex+a有6个零点.令t=|x-2|ex，则g(t)=t2-2at+a，首先研究t=|x-2|ex=|(x-2)ex|，只需研究y=(x-2)ex，由y′=(x-1)ex，当x∈(-∞,1)时，函数y=(x-2)ex单调递减；当x∈(1,+∞)时，函数y=(x-2)ex单调递增，又因为f(2)=0，则可以绘制函数y=(x-2)ex的草图如图1，又因为x=1时，y=-e，所以可以通过图象的变换得出t=|x-2|ex=|(x-2)ex|的草图如图2.

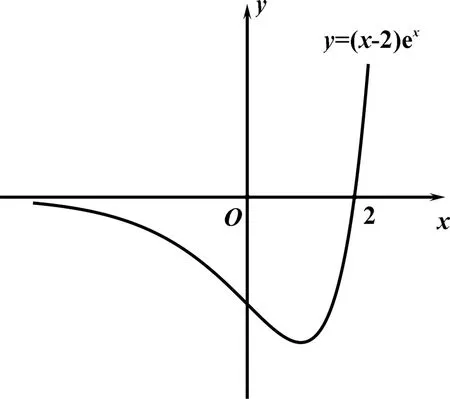
图1

图2

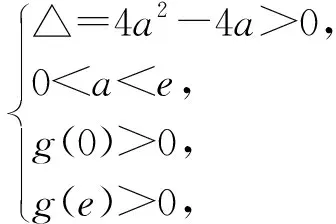
评析：求解本题的关键有两个方面，一方面可以将函数f(x)的零点个数转化为函数g(x)的零点个数；另一方面是令t=|x-2|ex进行换元，构造一元二次方程即可求解问题.

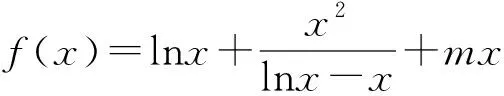
可见，利用换元法解决这类指数函数与对数函数混合不等式问题或函数零点问题，可以带来极大地便利.

好题总是回味无穷，耐人寻味，高考题深入展示了化归与转化思想、函数与方程思想、换元思想在不等式的证明中的运用.在教学中，我们应该经常与学生共享这些高考试题的思维探究和解法形成，引导学生探究解题方法，总结解题策略，对训练学生数学思维的广阔性、敏捷性、灵活性和深刻性是大有益处的.