一道导数多元变量不等式证明方法的深度融合
江苏省海门中学 (226100)
渠怀莲
多元变量不等式证明问题是导数中常见的一种题型,我们需要深入剖析,把握题目的本质,并对题目进行探究归纳,证明方法统一整合,与导数中单调性、极值、最值,切线基本问题融合考查.解决函数问题通常采用数形结合,正如著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微.”本文主要采用指对数的切割线放缩“以直代曲”思想方法论证不等式,并通过“数”进行逻辑推理,弱化条件或加强条件证明,化零为整统一结构形式,化整为零分而治之,构造新目标函数论证不等式.
一、题目呈现
已知函数f(x)=x(1-alnx)+1(a∈R).
(1)讨论函数f(x)的单调性;(略)
(2)若关于t的方程lnt-(m-1)t+1=0有两个不相等的实数根t1,t2,试证明:
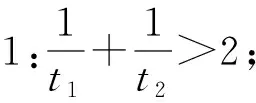
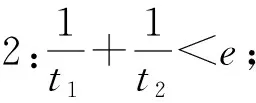

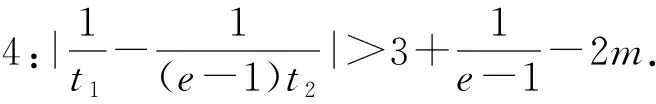
二、解法探究
首先,将方程调整至原函数的结构形式,利用已知结论解决问题,优化解题路径.

从而原问题转化为证明:
问题1:x1+x2>2;
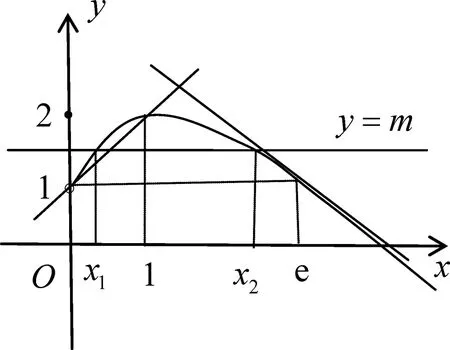
问题2:x1+x2 图1 其次,如图1,各参数的取值范围,1 最后,我们采用数形结合,先用“形”找出证明的突破口,再用“数”去论证推理. 问题1 (方法一)增量换元法,即将两个变量的和差积商作为一个变量,起到减元效果. (方法二)极值点偏移,由单调性重构函数证明不等式. 因为f(x)在(1,+∞)上单调递减,且0 问题2 以直代曲,切割线放缩. 图2 如图2以形助数,f(x)在(0,1)上考虑割线y=x+1,f(x)在(1,e)上考虑切线y=-x+e+1.首先,对∀x∈(0,1),都有f(x)>x+1.要证x(1-lnx)+1>x+1,即证xlnx<0,只需证lnx<0,成立.所以f(x1)>x1+1①.其次,对∀x∈(1,e),都有f(x)<-x+e+1,要证x(1-lnx)+1<-x+e+1,即证2x-xlnx-e<0.令φ(x)=2x-xlnx-e,1 问题3 (方法一)调整切线放缩,在区间内恰当选择切点. (方法二)弱化条件,尝试分而治之,重构函数证明不等式. 问题4 割线放缩,调整参数前的系数. 图3 此题的问题3是考查核心,其它几问是为了证明方法之间的融合而添加的设问.在证明过程中,我们采用了数形结合切割线放缩,其中寻找恰当的切点是关键,我们可以通过斜率去发现,也可以通过目标不等式中需要的量发现.方法一简洁明了,以形助数,“以直代曲”的思想方法,并且以数论形严密的逻辑推理.方法二技巧性要求很高,敢于把相关变量视作独立变量去处理,两个变量各重构一个新的目标函数分而治之.由此我们在处理数学问题时需要在“本手”的基础上,使出一招“巧手”,规避“俗手”解决问题的途径,做到知识与模块的整合,解决路径证明方法的融合,提升学生的直觉思维与逻辑思维.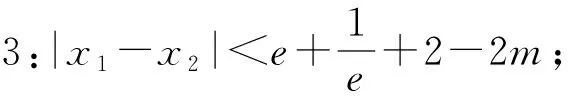




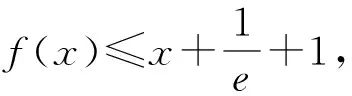



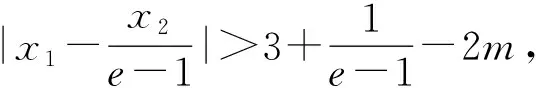
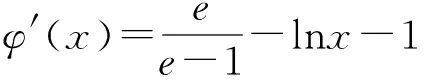
三、证后反思

