利用反比例函数图像对称性巧解题

林艺彬

(福建省漳州市第三中学 363000)

反比例函数是初中数学课程中的重要组成部分，同时对学生而言也是一个学习难点，其知识内容呈现出较为复杂抽象的特征.学习反比例函数的前提便是画好函数图像，在此基础上对函数图像的对称性进行研究，引导学生就函数图像对称性做到综合运用，对培养学生的数学思维与解题能力有着十分重要的作用.如今，伴随新课改的持续推行，针对反比例函数对称性解题的教学方法层出不穷，总体上都是向细致化与科学化发展，对教学实践起到了显著的促进作用.在此，笔者基于个人教学经验，同时借鉴一些成熟的教学案例，提出利用反比例函数图像对称性进行解题的具体方法，仅供参考.

1 反比例函数图像的对称性

2 利用反比例函数图像对称性进行解题的具体方法

2.1 图象为中心对称图形，对称中心是坐标原点

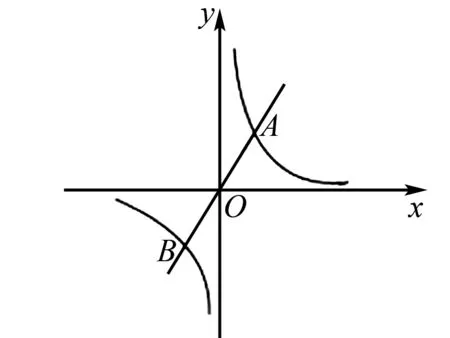
图1

A.(-2，-3) B.(2,3)

C(-2,3) D.(2.-3)

2.2 图象为轴对称图形，对称轴为直线y=x或y=-x

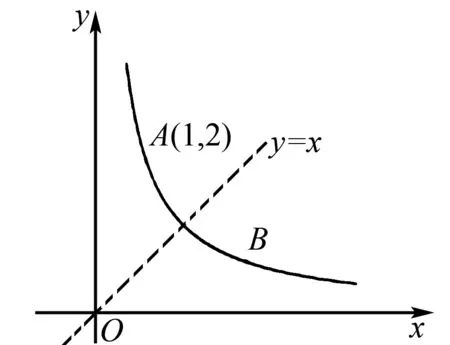
图3

解析基于点A与点B关于直线y=x对称的已知条件，可互换横纵坐标，即(a，b)变换为(b，a).已知点A的坐标为(1,2)，那么点B的坐标为(2,1).

结论2反比例函数图象关于直线y=x对称，其对称点为A(a，b)、B(b，a)，呈现出横纵坐标互换的点坐标特征.

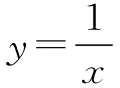
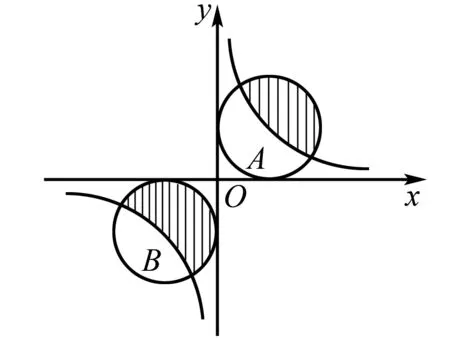
图4

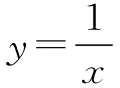
结论3反比例函数图象关于直线y=-x对称，其对称点为A(a，b)、B(-b，-a)，呈现出横纵坐标互换且互为相反数的点坐标特征.

3 反比例函数与几何综合题的方法分析

反比例函数与几何综合有着密不可分的关系，针对于这种类型的题目，教师可引导学生从以下几种思路来进行处理：一是就关键点处入手，基于关键点坐标及线段长度的相互转化，将函数特征和几何特征相结合而展开研究；二是围绕函数特征与几何特征进行组合、转化及列方程求解，如果能够有效利用反比例函数的模型，便可快速实现将函数特征向几何特征转化的目的.

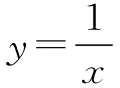
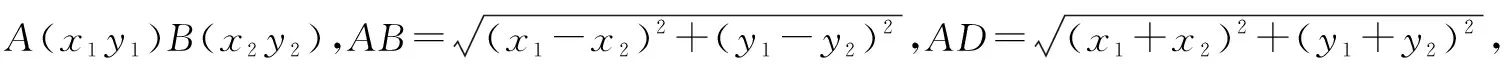
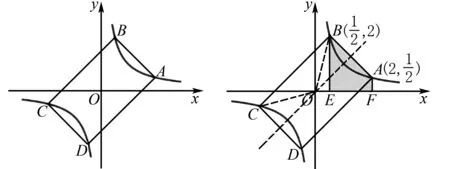
图5 图6

4 反比例函数图像对称性解题的教学方法

4.1 加入实例，增强学生反比例函数概念认知

在实际教学中，我们发现许多学生的记忆力都是很好的，可将教师在课堂上讲解的概念内容及时地记忆下来，但之后由于未能掌握相关学习方法且不愿意动脑，对数学学习便逐渐丧失了兴趣.数学教育并非是以单纯引导学生记忆数学概念与公式为主要目的，教师要通过教学让学生感到数学学习是一种乐趣、一种享受.如此，教师便要致力于激活学生的思维能力，调动学生学习兴趣，将难懂的反比例函数概念与实例相结合，帮助学生更好地理解与分析，减轻知识学习难度.以实际事例展开教学可丰富课堂内容与增强课堂教学的趣味性，而学生在不断地数学学习中也会实现数学思想的有效掌握，有利于其综合素养的培养.

4.2 引导积累，提升学生学习主观能动性

反比例函数对称性的相关理论知识的抽象性与复杂性极强，并不是仅凭几节课或是一段时间就能让学生完全领悟的，甚至于到了知识综合应用的解题环节，更是需要学生拥有较高的知识储备与应用能力.如此，教师便要引导学生去不断积累知识，同时做到长时间的坚持不懈，依照实际教学情境将反比例函数对称性的相关知识很好地融合起来，不断提升其个人认知，获知反比例函数对称性的实际价值与意义，这样一来，便能很好地提升学生学习的主观能动性.具体教学中，教师需要为学生提供一个自由、独立的学习空间，鼓励学生进行自主学习，而方法、教师都是其学习中的引导者，要为其发展提供关键力量.如可采用课题研究的教学模式，要求学生就反比例函数对称性的问题进行思考与探讨，将自身的想法与经验表达出来，同时吸收他人的宝贵意见，营造出一种团队合作与竞争的氛围.最后，还要把各个小组的劳动成果进行展示，先让学生进行自我点评，然后老师进行引导，这样不但突出了学生的主体地位，还实现了教师的引导作用.

总之，反比例函数图象的对称性是学生解题中一个重要的性质，若灵活运用此性质，必然能够及时、正确地解决题目，进而为反比例函数相关知识的学习提供很大的方便.对此，教师应在充分把握反比例函数图象对称性这一性质的基础上，通过结合实际例题与运用合适的教学方法，帮助学生更好地理解、掌握反比例函数图像的对称性性质，培养其解题思维，切实促进初中生数学核心素养的发展.