以中考题为例浅谈分类讨论在几何动点问题中的应用

张晓会

(广东省中山市第一中学 528400)

对于几何中的动点问题，我们不妨借助作图软件，根据动点所处的不同位置或者问题本身的可能性来做出相应的图形，进行分类讨论，再结合几何语言进行表述.这就要求我们首先找出整个动点的范围，和动点位置改变所对应的节点，然后再结合题目条件和不同情形的图形，应用相关知识计算出所求的量.

本文以近三年中考压轴题为例，说明分类讨论思想在几何动点问题中的应用，并作出变式辅以相应的图形进行说明.

例1 (2018中山)如图，已知Rt△OAB中，∠OAB=90°∠ABO=30°斜边OB=4，将Rt△AOB,绕点O顺时针旋60°，连接BC.

图1

(1)∠OBC=____°；

(2)连接AC，作OP⊥AC垂足为P，求OP的长度；

(3)点M，N同时从点O出发，在△OBC边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，记运动时间为x秒，△OMN的面积为y，求当x为何值时y可取得最大值？最大值是多少？

图2 图3 图4

本题考查了直角三角形、旋转以及二次函数最值问题等的相关知识，也可以相应改变图形和一些条件做相应变式练习，将“∠ABO=30°”改为“∠ABO=45°”和将“Rt△AOB绕点O顺时针旋60°”改为“Rt△AOB绕点O顺时针旋45°”，其余条件不变，依次求上述三个问题.

例2(2019中山)如图5，在△ABC中，AB=AC，AD⊥AB于点D，BC=10cm，AD=8cm．点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，记运动时间为t秒(t>0)．

图4 图5

(1)当t=2时，连接DE、DF，求证：四边形AEDF为菱形；

(2)在运动过程中所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长；

(3)是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值；若不存在，请说明理由．

(1)证明：略．

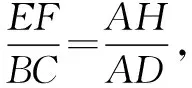
图7 图8

③若点P为直角顶点，如图8所示．

本题考查了菱形、三角形面积、二次函数最值、勾股定理等的相关知识，也可以改变图形和一些条件做相应变式练习：将“AB=AC”去掉，将“BC=10cm”改为“BD=4cm，DC=6cm”，其余条件不变，依次求上述第二、第三个问题.

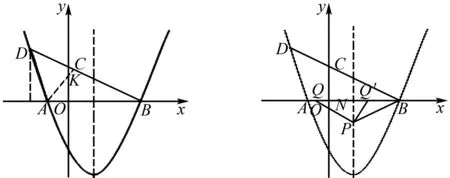
图9 图10

(1)求b，c的值；

(2)求直线BD的函数解析式；

(3)点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当△ABD和△BPQ相似时，请直接写出所有满足条件的点Q的坐标．

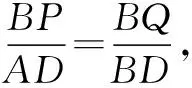
由以上几个中考题不难看出，几何动点问题经常会用到分类讨论这一数学思想，这就要求我们在平时的教学中不仅要注意学生基本的运算、推理能力的培养，更要有意识、有目的、有步骤地培养学生观察问题、分析问题的能力和思考能力，让学生体验数学的严密逻辑性，进而形成科学严谨的态度.