例析对二次函数综合问题的突破策略
陆兰兰
(江苏省常州外国语学校 213000)
二次函数是初中数学的重点与难点,其中综合类问题在中考中常作为压轴题出现.为使得学生在解题中少走弯路,提高学生解答二次函数综合问题的能力,应将其作为一个专题进行系统讲解.二次函数综合问题主要包括:图形周长问题、图形面积问题、角度关系问题、点的坐标问题、图形形状判断问题、参数定值问题六类,为使学生更好地掌握解决上述综合的问题的思路与方法,教学中应围绕具体例题展开教学活动.
1 二次函数与图形周长问题
二次函数与图形周长问题常依托二次函数性质考查一些特殊图形周长的计算.其中一些涉及周长最值的问题往往会考查圆的性质以及路径最短模型.突破该类问题不仅需要熟练掌握各种图形周长的计算方法,而且需理解与掌握相关模型的计算过程,透过现象看本质,结合习题创设的情境迅速构建熟悉的模型,使得问题得以顺利解决.
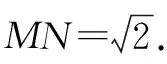
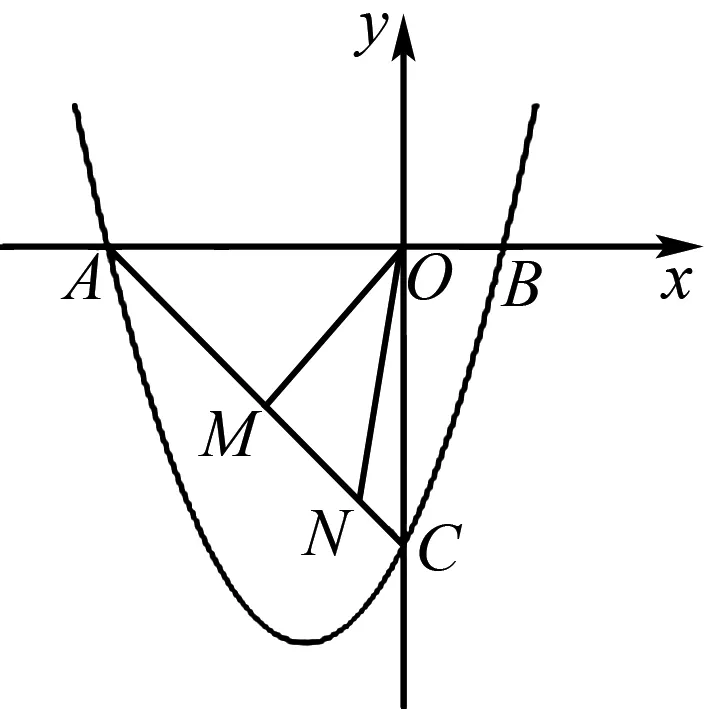
图1
(1)求抛物线的表达式;
(2)求△OMN周长的最小值.
对于问题(1)根据给出的顶点坐标,设出抛物线的顶点式方程,将已知点坐标代入求得具体表达式.问题(2)运用二次函数方程求出相关点坐标,设出点M的坐标后,充分挖掘题干中的隐含条件,找到MN两点坐标之间的关系,将问题转化为求直线同侧两点到直线上一点距离之和问题,借助路径最短模型计算出结果.
解(1)设抛物线的表达式为y=a(x+1)2-4,将点A(-3,0)代入得4a-4=0,a=1,则抛物线的表达式为y=x2+2x-3;
(2)令x2+2x-3=0,解得x1=-3,x2=1,则A(-3,0),C(0,-3),则容易求解出直线AC的方程为y=-x-3.设M(t,-t-3)(-3 图2 二次函数与图形面积问题是初中数学的常考问题.计算图形面积时如若为规则图形可联系规则图形面积计算公式进行计算.对不规则的图形常采用两种方法进行处理:方法一,将不规则图形分割成若干规则图形;方法二,借助图形之间的关系通过图形面积相减间接得出结果.如此便可将该类综合问题转化为求线段长度问题,借助题设条件以及二次函数图象特点,不难求出最终结果. 例2已知直线y=x-3和x轴、y轴分别交于A、C两点,点B(1,0),抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,对称轴与x轴交于点E,点E关于原点的对称点为点F,如图3,连接CE,P为直线y=x-3上的一个动点. 图3 (1)求抛物线的表达式; 问题(1)根据题干描述求出A、B、C三点坐标,运用待定系数法求解;问题(2)运用二次函数方程以及题干中的已知条件求出点P坐标以及直线PN的表达式.将直线和抛物线方程联立,求出点M和点N坐标,将△AFN,△BFM面积作差得出四边形ABMN的面积. 图4 二次函数与角度关系问题是初中数学各类测试中的常考问题.解答该类问题的思路是,首先运用几何性质分析线段之间的长度关系得出对应角度的大小,如等腰直角三角形、等边三角形、圆直径所对的圆周角等;然后借助锐角三角函数值进行逆向推理得出对应的角度.对于角度之间的关系,可运用三角形内角和,外角定理进行分析. (1)求抛物线的表达式及点M的坐标;(2)向下平移直线AB,得到过点M的直线y=mx+n,且和x轴负半轴交于点C,取点D(2,0),连接DM,求证:∠ADM-∠ACM=45°. 问题(1)根据直线方程求出点A坐标结合抛物线过原点得出表达式.问题(2)根据直线平移后的题干求出平移后的直线方程,然后通过求出对应线段长度得出∠DMH的正弦值以及对应角度大小,在此基础上运用外角定理证明得出结论. 二次函数与点的坐标问题常结合相关图形进行设问,要求学生计算出满足某一条件的点的坐标.解答该类问题思路因题而异,如要求满足某个图形形状时则需运用图形性质,当为直角三角形时应注重勾股定理的应用,判断线段、角度关系得出点的坐标.要求满足某个图形周长、面积问题时需要表示出对应的周长、面积.对于一些最值型问题需借助二次函数性质,确定具体坐标来解答. 综上所述,二次函数综合问题难度较大,教学实践中既要做好相关问题类型的归纳与总结,以及不同类型问题求解过程的讲解,又要要求学生做好听课笔记,把握解决不同综合问题的细节,并在课下开展针对性的训练活动,更好地巩固所学知识,锻炼解题灵活性,实现解题能力的进一步提升.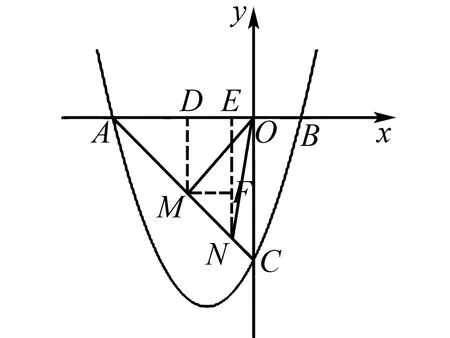
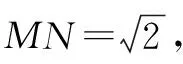
2 二次函数与图形面积问题
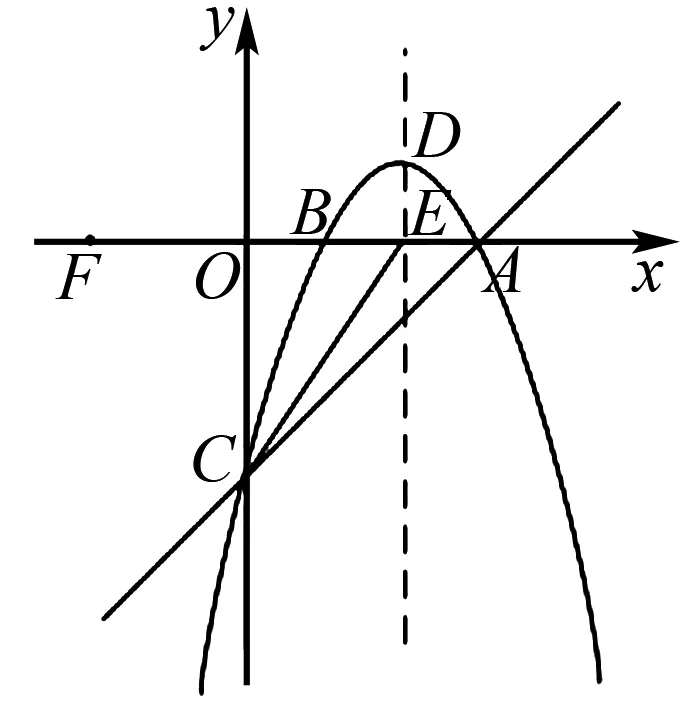
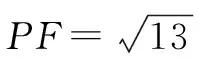
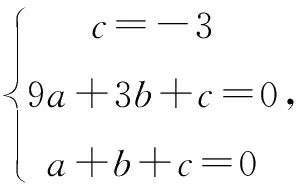
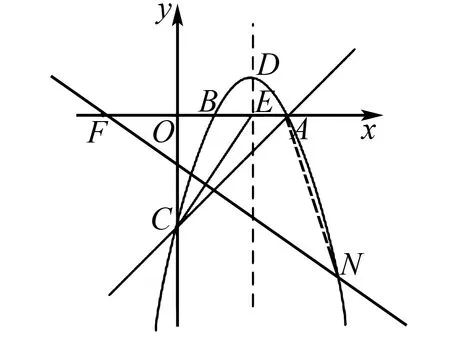

3 二次函数与角度关系问题
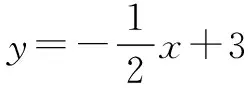
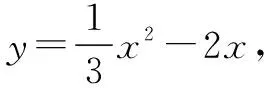
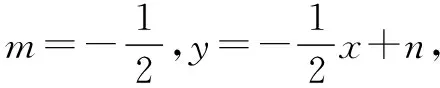
4 二次函数与点的坐标问题

