基于MPC的智能车辆变轨迹跟踪控制研究

贺晓丽

（天津职业技术师范大学，天津 300222）

0 引言

轨迹跟踪作为研究智能车辆的一部分，其作用是帮助智能车辆按照规划层规划出的轨迹路线稳定、精确行驶，将智能车辆的“想法”变成“现实”的执行环节。目前，已有众多学者对智能车辆的轨迹跟踪模块进行了深入研究[1-4]。张灏琦[5]针对智能车辆在低附着系数路面等环境下轨迹跟踪的精确性差以及稳定性不高的问题展开了研究，对传统LQR（线性二次型调节）的方法进行了优化，提出的前馈LQR算法提高了轨迹跟踪的精度。吴飞龙[6]针对高速工况下、低附着系数的复杂路面上转向和行驶稳定性等难以控制的问题，在传统MPC控制器的基础上设计了前轮主动转向控制器，对控制器参数进行了优化，并进行了实验验证。于向军[7]针对环卫车辆周期重复性工作特点，考虑模型时变以及未知扰动问题，提出了一种基于无模型自适应迭代学习的环卫车辆轨迹跟踪控制方法，提高了轨迹跟踪的精度。

综上可知，众多学者在轨迹跟踪这方面的研究一般是针对追踪单轨迹而言，单纯追踪圆形轨迹或者单纯追踪五次多项式轨迹，又或是在追踪单条轨迹的条件下研究不同工况下的追踪情况，但是针对变轨迹跟踪问题的研究尚未涉猎。因此对智能车辆进行变轨迹跟踪研究。基于传统的MPC（模型预测控制）控制器设计一种轨迹跟踪控制器，使得所设计的控制器应用于智能车辆时能够先进行5次多项式的单行换道然后继续追踪一定半径的圆形轨迹行驶。

1 车辆运动学模型

选择二自由度车辆运动学模型，以后轮轴心为参考点建立车辆运动学模型，如图1所示。

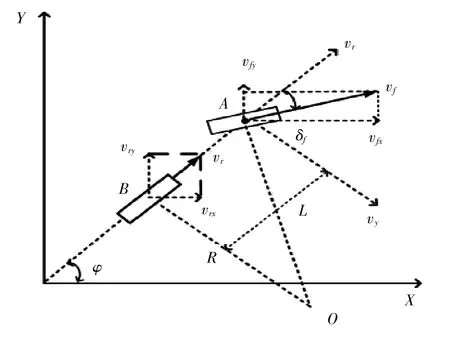
图1 二自由度车辆运动学模型

图1为依据阿克曼转向定理得到二自由度车辆运动学的简化模型。A点为前轴中心点，B点为后轴中心点，vr为后轮速度，vf为前轮速度，δf为前轮转角，L为轴距，O为瞬时转动中心，R为转动半径，φ为横摆角。

根据几何图形、理论力学以及高中的知识分析图1，可得到该二自由度的车辆运动学模型的状态空间表达式（1）：

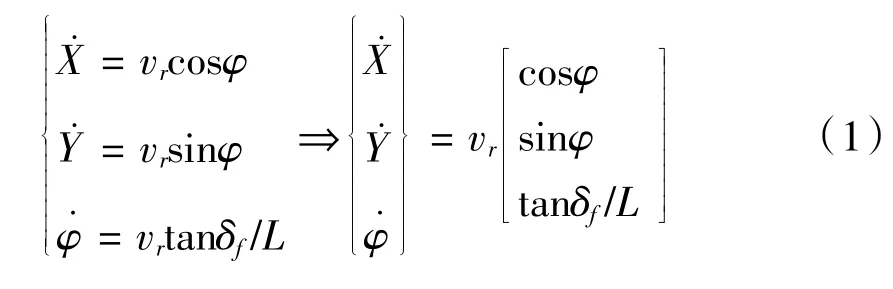
2 MPC轨迹跟踪控制器设计

分析MPC的原理，设计一种智能车辆轨迹跟踪控制器，使得所设计的控制器应用于智能车辆时能够先单行换道然后继续追踪圆形轨迹。设计步骤如下：

2.1 线性误差模型的建立

由车辆运动学模型的状态空间表达式（1）可设立该系统的状态量为X=[x，y，φ]T，控制量为u=[vr，δf]T，运动学形式写为：

设立参考系统的运动学形式为：

其中参考状态量Xr=[xr，yr，φr]T，参考控制量ur=[vr，δr]T。

（1）线性化处理

将式（2）在点（xr，ur）处采用一阶泰勒展开，只保留一阶项，忽略高阶项。泰勒公式为

得到

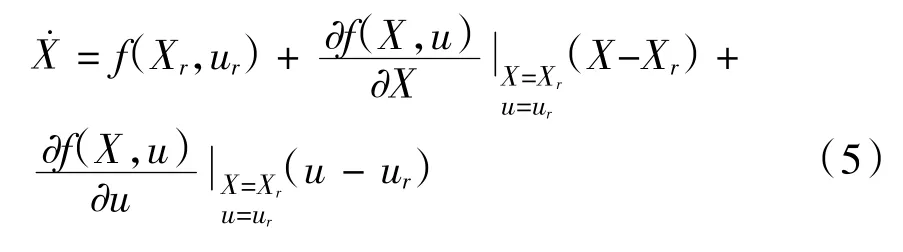
将式（5）与式（3）相减得到：

将式（6）写为

式（7）则为车辆运动学模型的线性误差模型。

（2）离散化处理

对式（7）进行前向欧拉离散化：

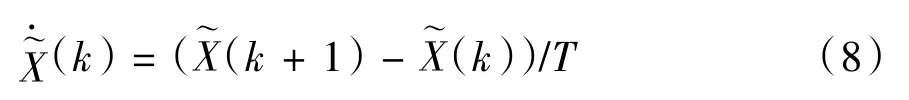
得到

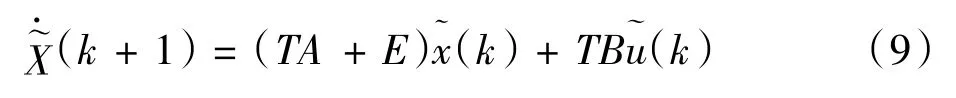
令TA+E=a，TB=b，则得到离散状态空间方程

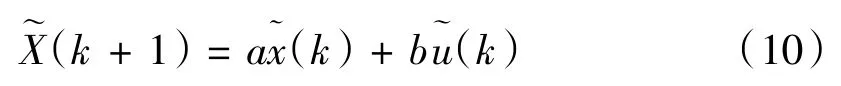
（3）构建新的状态空间方程

为了将状态量偏差和控制量偏差都整合进去，构建新的状态空间方程

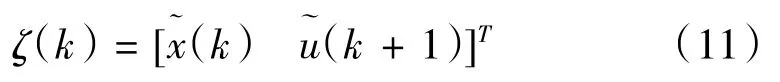
将式（11）迭代一次得到式（12）：

2.2 预测方程

预测时域Np≥控制时域Nc。将式（12）进行迭代得到：

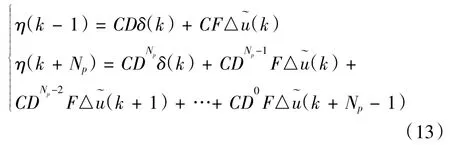
得到预测方程

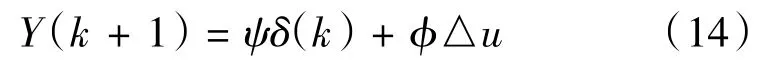
由式（14）可知下一时刻的输出量等于该时刻的状态量与该时刻控制量的变化量之和，求解出控制量的变化量即可预测出下一时刻的输出量。

2.3 优化

为求解控制量的变化量，将求解问题转化为二次规划问题。构建代价函数为

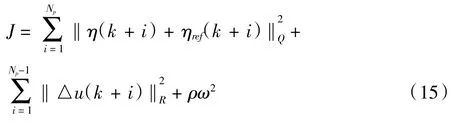
式中ρ为权重系数，ω为松弛因子。

2.4 约束

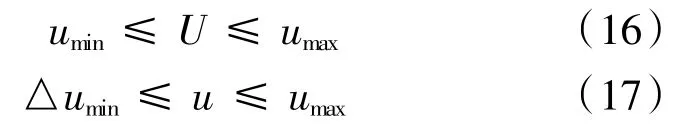
利用硬约束和软约束对控制增量进行求解，将约束条件转化为控制增量的形式，得到转换矩阵的形式为：

求解出控制量变化量的矩阵序列，将求解的结果代入误差方程进行滚动优化。如此循环往复。

3 Carsim-Simulink联合仿真

利用Carsim和Matlab中的Simulink模块建立Carsim-Simulink联合仿真实验平台。

3.1 在Carsim中选取智能车辆

选取智能车辆如图2所示。

图2 所选智能车辆图示

选取智能车辆的相关参数设置见表1。

表1 智能车辆的参数设置

3.2 设置实验条件

智能车辆的起点设置为原点，参考轨迹设置为五次多项式的单行道换道然后进行圆形轨迹的变轨迹路线。采样时间设置为0.01 s，仿真时间为30 s，松弛因子的值为10，参考变轨迹的前轮转角为0。

3.3 仿真验证环节

建立Carsim与Simulink联合仿真的平台。选择Carsim软件提供的一部车型，输入输出参数进行设置，完成Carsim与Simulink接口设置。将智能车辆模型发送至Simulink中；在Simulink中搭建模型，将设计的轨迹跟踪控制器算法嵌入S-Funcation模块实现程序。验证结果如图3所示。

图3 追踪变轨迹的实际位移与预设变轨迹位移对比图

由图3可看出，虚线代表所设计的参考变轨迹位移曲线，实线代表将所设计的MPC变轨迹跟踪控制器应用于该智能车辆时的实际追踪位移曲线。从图中观察可知，所设计的变轨迹MPC轨迹跟踪控制器应用于该智能车辆时能够很好地完成先单行换道又继续追踪圆形轨迹的追踪任务及能够比较精确的追踪上所设计的变轨迹曲线，从而证明该控制器具有适应变轨迹追踪的可行性。

如图4所示为所设计的MPC变轨迹跟踪控制器应用于智能车辆时追踪所设计的变轨迹曲线时的横向位移对比曲线图，其中虚线部分为追踪变轨迹的参考横向位移曲线，实线部分为追踪变轨迹时的实际横向位移曲线。从图中观察得知，在0～15 s的单行换道时域内，实际轨迹与参考轨迹基本吻合；然后结束换道，在15～30 s时域内继续追踪圆形轨迹时同样具有良好的追踪性，实际横向位移与设计的变轨迹参考位移之间误差很小，误差基本稳定为0～0.5 m。

图4 追踪变轨迹的横摆角速度曲线图

综上可知，基于传统MPC轨迹跟踪控制器设计的一种MPC变轨迹跟踪控制器应用于智能车辆时能够成功完成先执行单行换道后继续追踪圆形轨迹的变轨迹任务。因此本设计的轨迹跟踪控制器具有适应变轨迹追踪的新型用途。

4 结论

（1）基于MPC原理，分析了传统MPC轨迹跟踪控制器的设计过程。通过建立二自由度的车辆运动学模型，经过线性、离散化处理得到线性误差方程；在此基础上进行迭代得到预测方程，将求解控制量的问题转化为二次规划问题，结合硬约束和软约束环节对该问题进行求解和滚动优化。

（2）在传统MPC轨迹跟踪控制器的基础上增加设计五次多项式和圆形轨迹相结合的变参考轨迹，并将该MPC变轨迹跟踪控制器嵌入Simulink中的S_Function模块。搭建了Carsim-Simulink联合仿真实验平台。验证结果显示：MPC变轨迹跟踪控制器应用于智能车辆时，能够完成先执行五次多项的单行换道，后继续进行圆形轨迹的追踪任务，证明该MPC变轨迹跟踪控制器具有适应变轨迹追踪的新型用途。