一种基于PCA和相关向量机的锂电池在线寿命预测方法研究
王国良,狄心莹
(辽宁石油化工大学信息与控制工程学院,辽宁 抚顺 113001)
锂离子电池作为电源系统的重要组成部件,其具有小巧轻便、环保节能、高续航能力等优点[1],被广泛应用于各大领域。为了促进新能源技术的发展,对锂离子电池的剩余寿命进行预测研究至关重要。以往对锂离子电池充放电过程的研究中发现,随着电池的使用时间和充放电循环次数的增加,其容量在不断减小[2]。为了避免对重要设备造成永久性损坏,必须对电池容量进行预测,从而保证电池在使用期间处于健康状态[3]。
锂离子电池的剩余寿命预测可分为基于概率统计分布、模型驱动和数据驱动预测方法[4]。数据驱动作为概率统计理论的主要预测方法,其结合神经网络和支持向量机(SVM)[5]等学习方法,通过建立输入和输出变量之间的模型来预测锂离子电池的剩余寿命。解冰[6]建立基于最小二乘支持向量机模型,引入遗传退火算法提高了预测精度。王瀛洲等[7]利用蚁狮优化和支持向量回归的方法提高了电池寿命预测准确性。倪裕隆[8]改进了蚁狮优化算法,为SVM方法提供最优参数,进一步提高了其预测精度。但是,支持向量机须选用满足一定约束条件的核函数,预测结果为无概率性表现形式,并且神经网络收敛速度慢,训练时间长,预测值为稀疏性的点估计值。引入贝叶斯思想后,弥补了该不足。但是,通常基于RVM相关的锂离子电池寿命预测方法只考虑单一变量的输入输出关系,对多变量输入与输出不能直接建立关系模型。对单一特征因素变量分别预测并加权融合得到的预测值,虽然在一定程度上提高了预测精度,但效果不够明显且步骤冗余。针对这一问题,本文提出了基于主元分析的特征因素变量加权的RVM锂离子电池剩余寿命预测方法,该方法的普适性更广,对锂离子电池的寿命预测精度更高。
1 基本原理和算法
基于相关向量机的锂离子电池寿命预测模型数据处理方法,对单一特征变量预测输出值加权和基于PCA的特征因素变量加权融合构建得到预测输出值。首先,对不同特征变量,通过相关向量机得到相应预测模型,考虑输出的各预测值向量之间线性相关性得到相应权值。然后,基于PCA思想,直接将不同特征变量对电池寿命衰减的影响程度作为给出权值的重要依据。
1.1 PCA的数学意义
假设对系统的n个采样点进行m次独立采样,则系统可以由一个n×m维的随机矩阵G∈Rm×n描述。
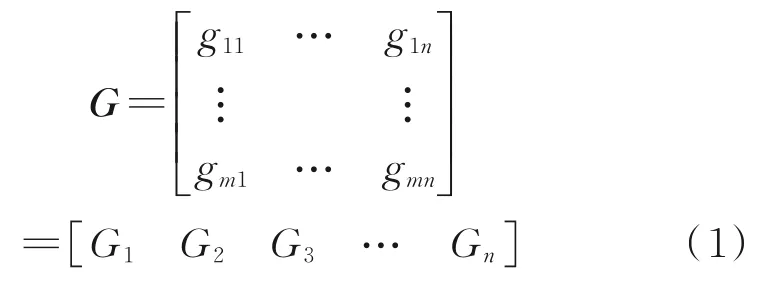
式中,gi,j为采样数据变量,i=1,…,m;j=1,…,n。
由于所采集的数据中包含不同量纲,为消除带有不同量纲的数据所组成的数据矩阵对PCA的运行结果有所影响,先对G进行归一化处理,去除系统数据的量纲。
1.1.1 归一化处理 通过式(2)对数据进行归一化处理。
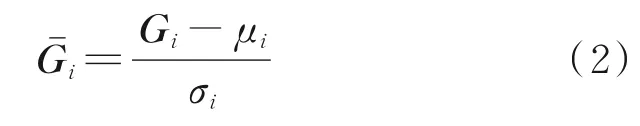
式中,为对向量Gi归一化处理后的得到的新数据向量;μi和σi分别为Gi的均值和方差。通过处理,可得随机矩阵

随机矩阵可以分解为n个向量的外积之和,即:
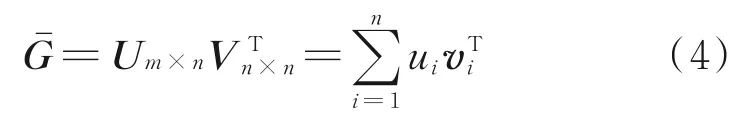
式中,Um×n=[u1,u2,…,un]为得分矩阵,由得分主元ui∈Rm×1构 成;Vn×n=[v1,v2,…,vn]为 负 荷 矩阵,由负荷向量vi∈Rn×1构成,且由矩阵Gˉ的协方差矩阵给出。
1.1.2 特征值与特征向量 记上述随机矩阵Gˉ的协方差矩阵为ΣGˉ,则:

对式(5)求解:
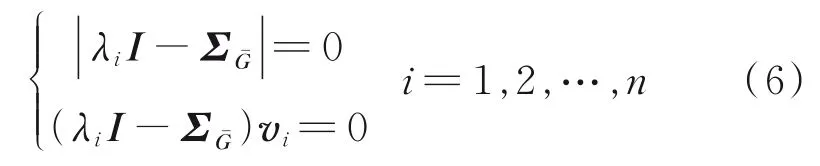
式中,λi为特征值;I为特征向量。
求解后可以分别得到协方差矩阵ΣGˉ的特征值λi(i=1,…,n)及相对应的特征向量vi(i=1,…,n)。通常假设n个特征值都不相等,并且有λ1>λ2>λ3>…>λn。为证明式(4)成立,两边同乘以vi得:
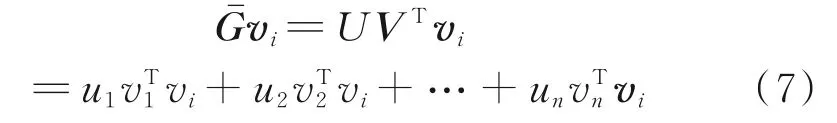
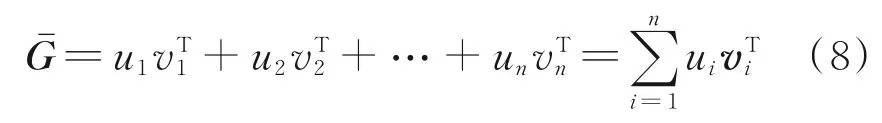
1.1.3 确定主成分个数 一般情况下,设主成分个数为k(k≤n),且k满足:

求得k,那么矩阵则可表示为:

式中,̂为主成分空间(主元空间)为残差空间。
在现代工业控制研究中,PCA常与其他方法结合应用于各领域控制系统的在线故障检测问题研究[9-10]及其他方面的数据分析中。T2和SPE是PCA中两个常用的性能指标,用于故障诊断。
1.2 相关向量机
相关向量机(RVM)[11]是在SVM的基础上做相应的改进,由E.M.Tipping[12]在2001年提出的。
假设存在训练样本集{xk,yk},(k=1,2,…,n),其中xk为输入向量,yk为输出向量,并认为yk是关于xk的函数ϕ(xk)的输出,即:

式中,εk为方差σ2的高斯噪声,服从均值为0。常见的ϕ(xk)形式为:
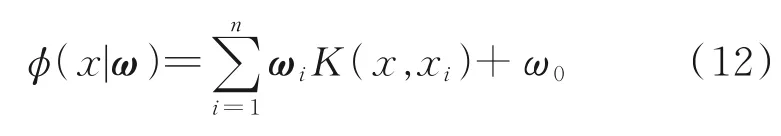
式中,ω=(ω1,ω2,…,ωn)为权重向量;K(x,xi)为核函数;ω0为偏差[13]。E.M.Tipping从贝叶斯理论的角度出发,认为ω服从先验分布,即
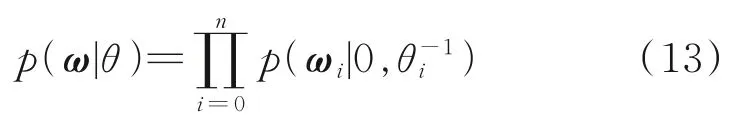
可以得到权重向量的后验分布:
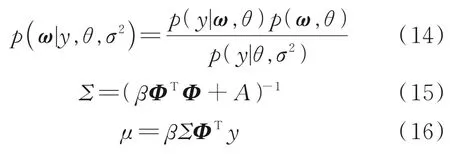
式中,Σ为后验分布方差;μ为后验分布均值;y为训练 样 本 的 输 出 量;A=diag(θ1,θ2,…,θn),Φ=[ϕ(x1),…,ϕ(xn)]T为设计矩阵,ϕ(x)=[1,K(x,x1),…,K(x,xn)]T。超参数的θ和方差σ2优化可以通过式(17)和式(18)实现。
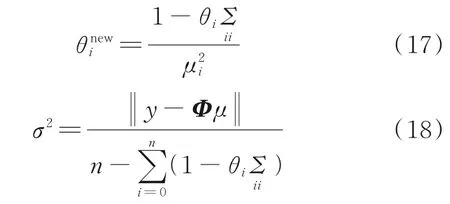
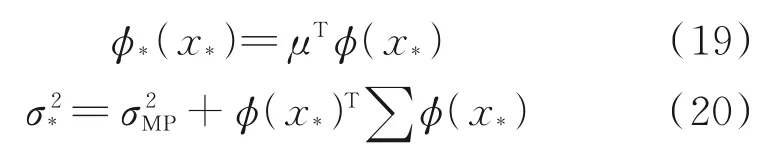
选取RBF核函数[14],该核函数具有使特征输入和输出样本呈现非线性的能力,仅在测试数据点的附近较小领域内产生影响,非线性逼近能力很强,其表达式为:
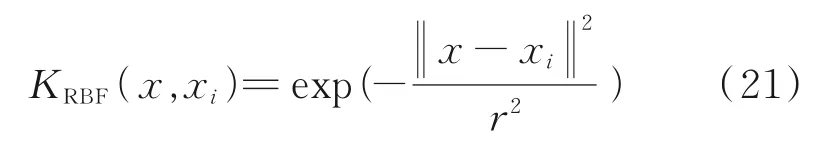
式中,r为核函数的参数。r越小,RBF对原数据的影响范围越小。
1.3 基于PCA特征因素变量加权建构概述
1.3.1 单因素变量RVM预测值的加权处理 根据RVM理论基础,分别对可能影响锂离子电池容量的不同特征变量测量值与电池容量真实值建立RVM模型,得到所对应的预测输出y*。由于电池容量的变化非单独某个特征变量引起,不同y*和实际容量存在相应的线性关系:

式中,y*1,y*2,…,y*n分别对应n个特征变量;x1,x2,…,xn为RVM模型下的预测容量值;Y*为预测值线性融合向量,由预测值线性融合所得;ti为相应的权重系数,由向量相关系数给出:
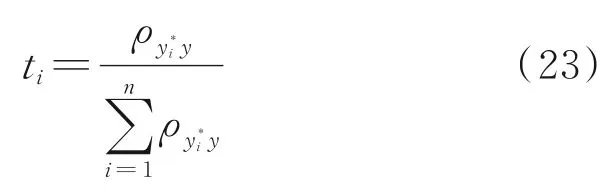
式中,ρy*y为表征电池容量预测值向量y*与真实值向量y之间线性关系的紧密程度指标(||ρ≤1),其绝对值决定二者之间的紧密程度,cov(·)为协方差为标准差。|ρy*y|较大,说明y*与y的线性相关程度较强;|ρy*y|较小,说明y*与y的线性相关程度较弱;|ρy*y|=0,则说明y*与y不相关。。
1.3.2 基于PCA的特征变量加权建构方法 根据PCA的数学意义可知,对采样特征变量原始数据矩阵G归一化去量纲处理后得到矩阵Gˉ,通过Gˉ求取协方差矩阵ΣGˉ,并计算该协方差矩阵特征值及与之对应的特征向量,可以找到表征变量主要特征的主元向量ui(i=1,2,…,m)。特征值决定主元的重要程度。

式中,ri为权重系数由协方差矩阵特征值给出:

该协方差矩阵特征值同样决定主元的重要程度,即主元向量对原变量向量的覆盖程度。因此,可以得到相关主元的权重系数,从而得到各特征因素变量加权构建以后的特征变量。将此变量作为锂离子电池在线剩余寿命预测相关向量机的输入,与真实电容值建立相应预测模型。对新采集的电池数据进行PCA分析,并对处理后的特征变量通过相关向量机进行在线预测,得到预测结果。具体流程如图1所示。

图1 PCA加权特征建构电池寿命预测流程
2 实验与分析
为了验证所提出的预测值加权构建及特征因素变量加权构建方法的性能,证明两种方法的有效性,选取B7型号锂离子电池实验所得数据,采用两种方法进行仿真实验。对已有的相关研究分析发现,锂离子电池在线运行存在不完全充放电的现象,因此需将数据中锂离子电池不完全充放电时数据全部剔除,对锂离子电池进行在线剩余寿命预测方法的研究才具有一定意义。等压升充电时间间隔、等流降充电时间间隔和等压降放电时间间隔三个特征因素变量可作为主要相关向量机建立模型的输入。提取可测量特征因素变量后,根据已有容量数据,通过相关向量机(RVM)建立特征因素变量与电池容量的关系模型;将在线采集的特征变量数据向量作为输入,输出得到相应的容量预测值向量。充电时,电压从2.7 V上升到4.2 V所需时间作为特征因素变量x1,即x1为等压升充电时间间隔;电流从1.5 A下降到0.3 A所需时间作为特征因素变量x2,即x2为等流降充电时间间隔。放电时,电压从3.7 V下降到2.7 V所需时间作为特征因素变量x3,即x3为等压降放电时间间隔。
综上,提取等压升充电时间间隔等三个特征因素变量及相应的电池容量数据进行实验分析。实验所用数据均采用NASA公布的B7号锂离子电池的164组充放电循环真实测量数据。
2.1 预测值加权构建
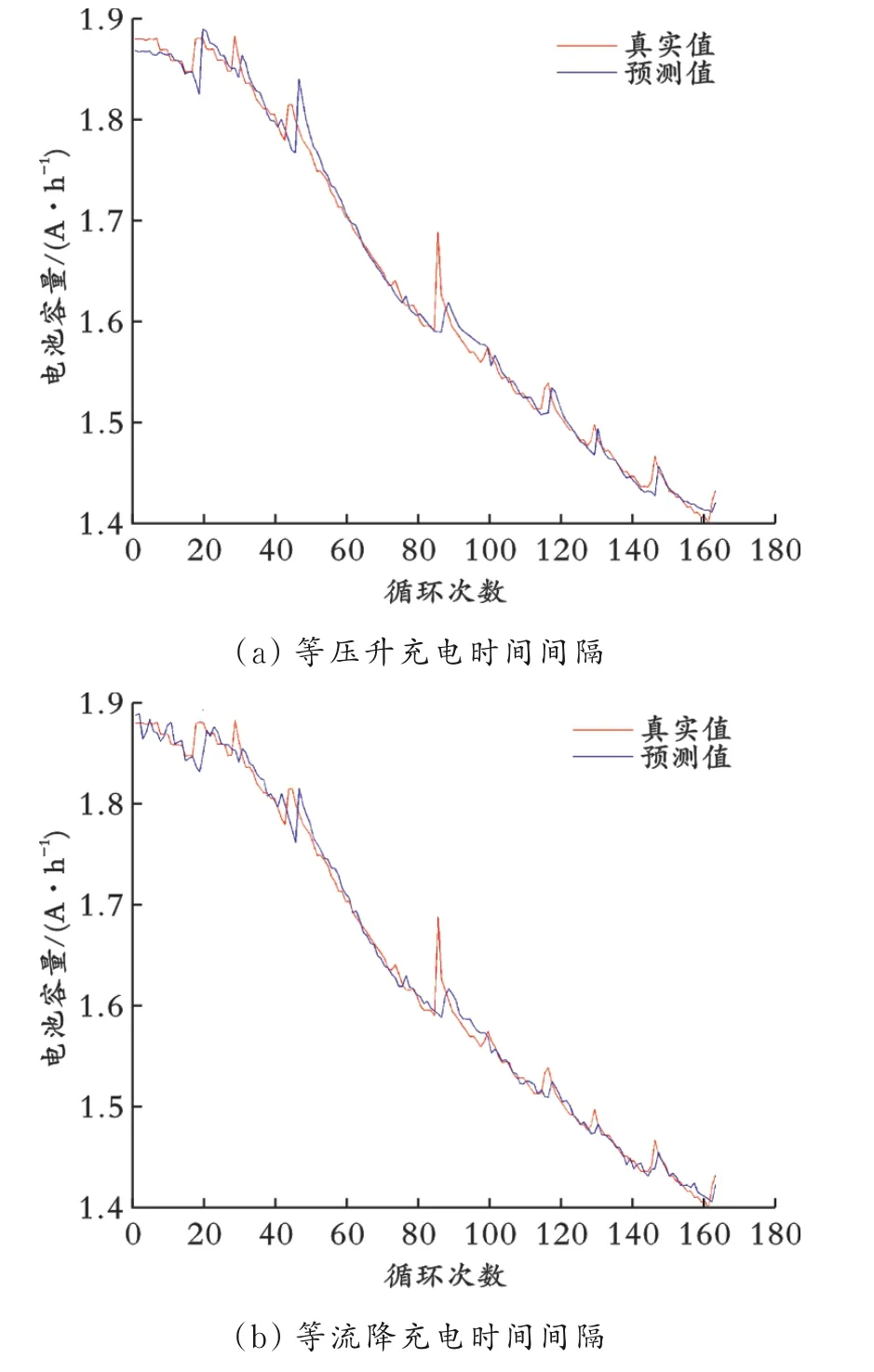
分别利用B7号锂离子电池的三个特征因素变量x1、x2、x3进行预测,所得预测值由相关系数线性融合所得值与融合前的三组单一变量预测值进行对比,其中选取前100组建模数据作为静态数据,用于建立预测模型。模拟建模完成后,采集的新产生64组数据设为动态采集数据,用于在线预测,预测起点为101。
单一变量及预测值加权建构预测结果如图2所示。预测输出Y*由预测值线性融合所得。预测值从101循环开始,64组预测数据实验分析结果为对不同单一特征因素变量预测结果线性拟合得到的加权预测值,考虑了多个特征因素变量对电池容量衰减的影响。对比单一特征因素变量建立的预测模型机制,由数学增长率算法计算得拟合程度分别比单个特征变量的预测值拟合程度提高2.3%、0.4%、0.7%,在一定程度上增加了其预测精度,预测值更加接近容量真实值,对提高锂离子电池在线寿命的预测性能具有一定意义。
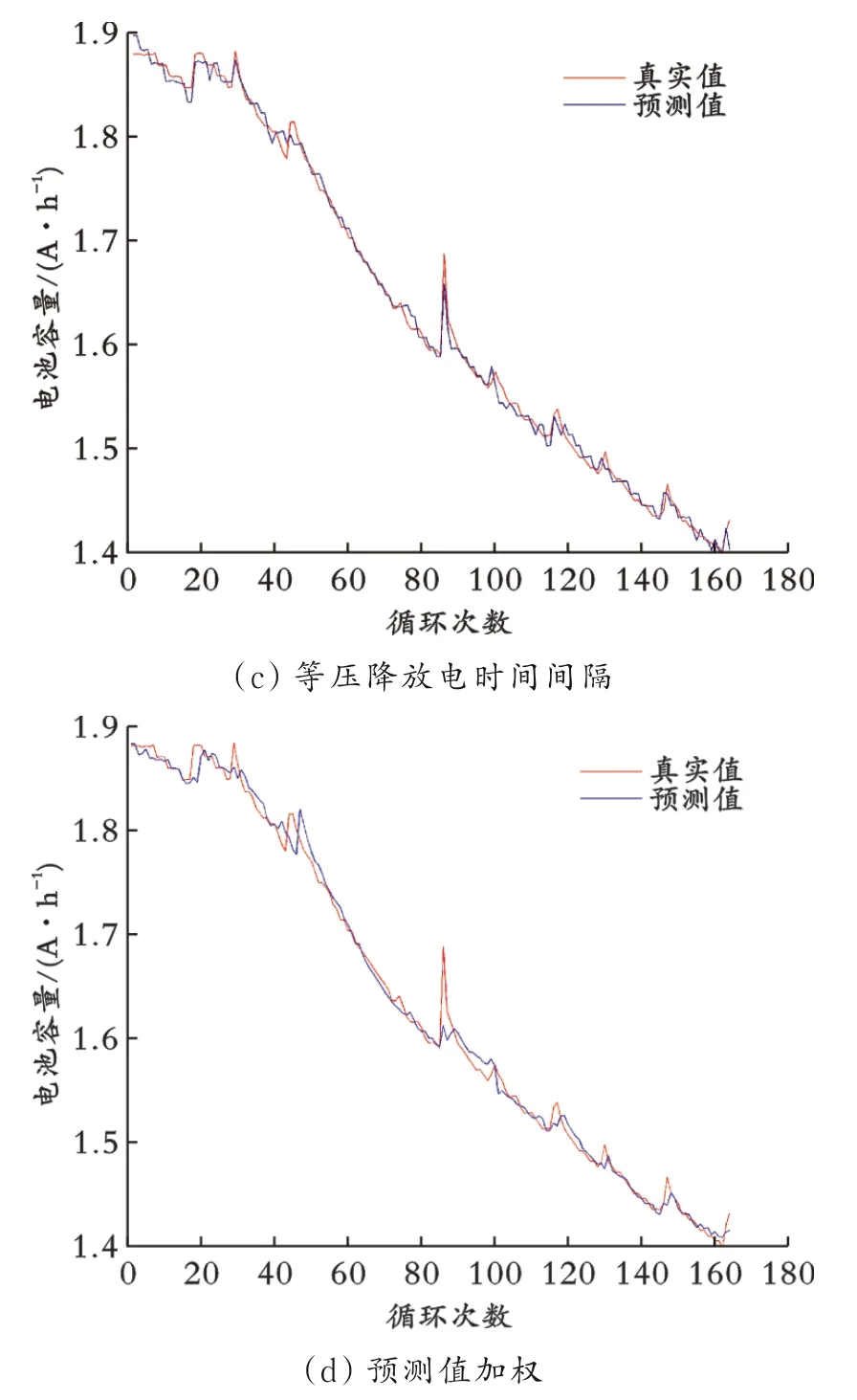
图2 单一变量及预测值加权建构预测结果
单一变量加权构建方法的预测效果如表1所示。
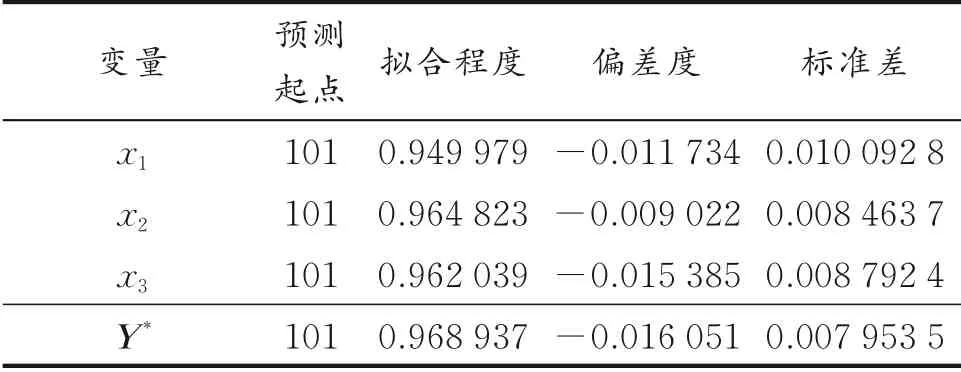
表1 单一变量加权构建方法的预测效果
2.2 基于PCA的特征因素变量加权建构
基于PCA的特征因素变量加权建构预测实验分析,采用B7号锂离子电池164组充放电循环真实数据进行实验分析。其中,选取前100组中3个特征因素变量数据作为静态数据,经PCA分析用于相关向量机建立电池寿命预测模型,得到其相应核函数参数,即通用程序里可调节参数a=3,J=1.8;取后64组设为动态采集数据,用于电池寿命的在线预测。在线寿命预测过程如下:
预测建模确定相关向量机核函数参数后,开始进行在线预测实验;读取第101组数据中3个变量值为第一组测量值,将所构成的1×3维向量型矩阵作为PCA的输入得到加权建构特征变量值,由相关向量机得到对应预测电池容量值;继而读取第102组数据,重复上述运算步骤,得到对应预测值;以此类推,分析计算第103,104,…,164组数据,依次得到相应电容的预测值,进而完成锂离子电池的在线寿命预测实验。
基于PCA的特征变量加权构建预测结果如图3所示。
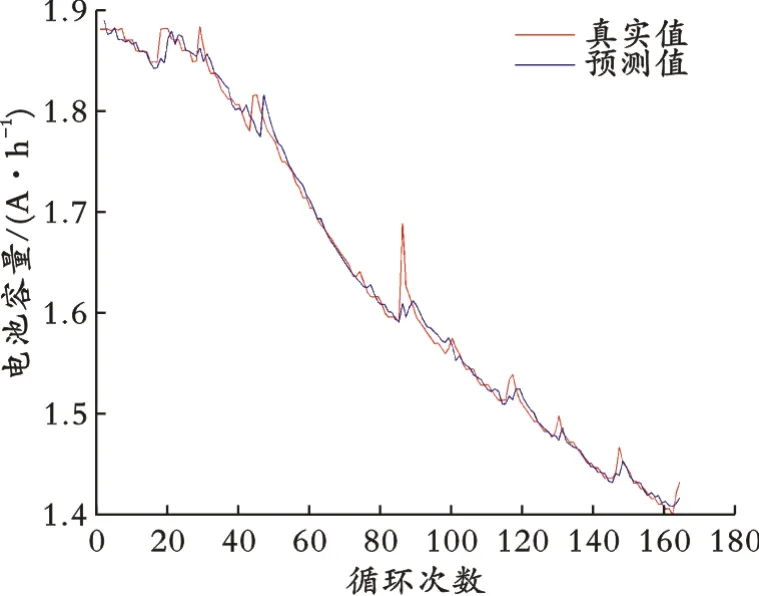
图3 基于PCA的特征变量加权构建预测结果
由PCA加权构建所得特征变量作为输入得到的电池容量预测值,避免忽略多个特征变量输入对锂离子电池容量衰减的影响,从根本上解决了多个不同特征因素变量对电池容量衰减影响程度不同而导致存在预测精准度差异的现象,拟合程度较比单个特征变量的预测值拟合程度分别提高2.3%、0.7%、0.9%,在一定程度上提高了其预测精度,使预测值更加接近容量真实值,有效地提高了锂离子电池寿命的在线预测性能。
PCA特征变量加权构建方法的预测效果如表2所示。其中,X*为PCA加权建构所得特征变量。

表2 PCA特征变量加权构建方法的预测效果
2.3 两种建构方法预测结果对比
预测值加权构建与基于PCA特征变量加权构建方法对锂离子电池容量预测结果(见图4)。
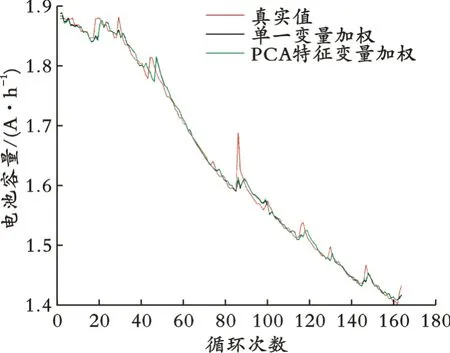
图4 两种预测结果对比
从图4可以看出,与单一变量加权构建方法相比基于PCA的特征变量加权构建方法的预测效果更好。
3 结论
多个单一变量预测值加权线性融合的方法,虽考虑到多个特征因素变量对电池容量衰减的影响,在一定程度上增加了预测精度,但仅适用于变量少的相关预测实验研究,普适性低。由PCA加权构建所得特征变量的方法进行预测,可避免不同特征变量对锂离子电池容量衰减的影响,同时从根本上解决因多个不同特征因素变量对电池容量衰减影响程度不同而存在预测精度差异的现象,增加其预测精度,使预测值更加接近容量真实值,普适性更高。验证实验结果表明,所提变量加权建构处理方法的预测结果与电池真实容量值拟合程度更好,证明所提方法的可行性和有效性。

