基于余氏理论及元胞自动机的Ti-2Nb合金组织模拟
林丽彬,林成,郭丽丽,莫永星,杨静怡,崔建潇,彭贤民
(1.辽宁石油化工大学 机械工程学院,辽宁 抚顺 113001;2.锦州锦恒汽车安全系统股份有限公司,辽宁 锦州 121007)
近α钛合金由于密度低、耐腐蚀性能好、焊接性好被广泛应用于船舶、海洋管道和化工行业[1]。Nb是钛合金中广泛使用的一种合金元素,具有β稳定化作用。同时,Nb元素固溶在钛合金中能够产生显著的固溶强化作用,在提高合金强度的同时,也能保持良好的塑性。因此,研究Nb元素对钛合金组织演变规律的影响,尤其是对其理论模型进行研究,对钛合金的合金化原理具有重要的价值。
目前,合金微观组织模拟方法主要有相场法(PF)[2-5]、蒙 特 卡 罗 法(MC)[6-10]和 元 胞 自 动 机 法(CA)[11-16]。这些组织模拟方法大体上可分为两类:一类为数值解析法,它是在经典的材料晶粒长大理论模型的基础上,利用数值计算方法对经典理论方程进行求解,从而实现组织模拟的方法;另一类为计算机抽象图形显现法,它是设计一定几何阵列来构造初始组织,然后依据材料晶粒长大的物理和数学规律,通过程序操作来完成组织模拟的方法,该方法侧重事件的随机性。由于后者比较方便、实用,因而得到广泛应用,如蒙特卡罗法和元胞自动机法。但是,如何对抽象的几何阵列赋予材料在设计、制备、相变及服役中的真实物理内涵,仍是研究者一直探讨的问题。近年来,大数据、机器学习和人工智能技术在国内外发展迅速,机器学习辅助材料设计与优化已成为材料研究的热点领域之一[17]。目前,以机器学习为代表的材料基因组工程[18]已经在功能材料领域获得比较成功的研究结果,但在结构材料方面仍需进一步深入研究。由于该方法依赖大量实验数据以及多学科方法手段,因此如何在分析模型中嵌入材料科学基本原理,仍面临诸多挑战。
吉林大学余瑞璜院士于1978年建立了固体与分子经验电子理论(简称余氏理论)[19],该理论已经广泛应用于材料领域,如相变[20-24]、结合能[25-27]、强韧化[28-30]、磁性[31-32]、界面[33-34]、复合材料[35]等。但是,基于余氏理论的合金组织模拟工作仍未深入开展。最近,辽宁石油化工大学合金价电子结构与成分设计课题组首次提出了基于余氏理论及元胞自动机开展钛合金β相组织模拟的方法[36]。但是,该方法主要适合多元钛合金的情况,对不含Al元素的钛合金体系(如二元合金)并没有给出具体方法。因此,本文利用文献[36]给出的方法思路,开展了Ti-2Nb合金β相高温固溶组织模拟研究,进一步阐明了不含Al元素钛合金β相高温固溶组织的模拟方法。本文给出的方法思路与实现途径,为丰富和发展基于余氏理论的组织模拟方法提供了重要的基础数据,具有一定的参考价值。
1 建模方法
Ti-2Nb合金在升温 过程中,α相逐 渐向β相转变。随着温度的升高,α相比例逐渐减少,而β相比例逐渐增多。当温度达到β相变点以上时,Ti-2Nb合金中α相全部转变为单一的β相固溶体。在固溶温度刚刚达到相变点以上时,Nb元素在合金中分配并不均匀,处于不平衡状态,随着固溶处理的持续,Ti-2Nb合金中Nb元素达到平衡。Nb元素在合金中再分配过程中,伴随着β晶粒形核和长大。Nb溶质原子固溶到基体β-Ti后,在其周围产生浓度梯度,形成有利于形核的位置。在这些有利形核位置中,有些相结构单元形成若干晶坯,并逐渐长大成细小晶粒,然后这些细小晶粒经过晶粒的吞并与长大,形成常见的等轴β相组织。基于上述金属学基本原理,开展了Ti-2Nb合金β相高温固溶组织模拟。
Ti-2Nb合金β相组织模拟的流程示意图如图1所示。图1中,a、b分别为β-Ti-Nb、β-Ti的结构单元;c为相结构单元随机分布图;d为形核点随机分布图;e为四邻居生长的细小晶粒;f为八邻居生长的晶粒组织。
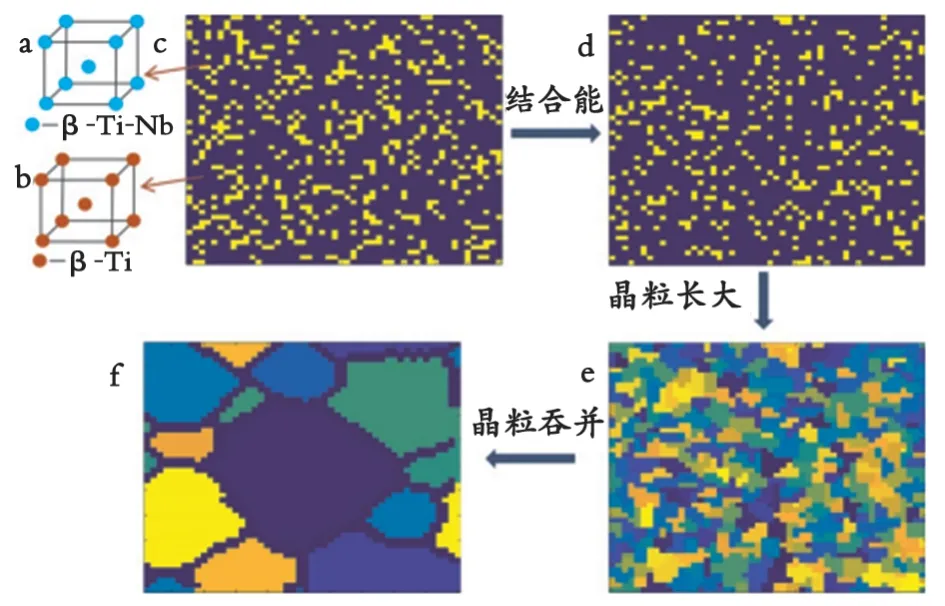
图1 Ti-2Nb合金β相组织模拟流程示意图
β相固溶组织(β相组织,下同)模拟的建模思路为:首先,构建β相结构单元模型,即Ti-2Nb合金高温固溶时β相组织由β-Ti、β-Ti-Nb结构单元混合而成(见图1中a及b),并且在β-Ti-Nb结构单元周围形成有利于形核的位置;其次,并不是所有的有利形核点都参与形核与长大,该过程与固溶温度及结合能大小有关,故利用余氏理论计算的相结构单元结合能计算β相组织演变时的形核点数目(见图1中c及d);再次,利用元胞自动机中的四邻居规则实现由相结构单元演变成微小晶粒的模拟(见图1中e);最后,利用元胞自动机中的八邻居规则实现微小晶粒吞并、长大过程,从而完成Ti-2Nb合金β相组织模拟(见图1中f)。
具体建模方法如下:假设Ti-2Nb合金在高温固溶时β相组织中含有β-Ti、β-Ti-Nb相结构单元,并且通过Ti-2Nb合金的名义成分获得β-Ti-Nb结构单元的可能份额Fβ-Ti-Nb,其计算公式为:
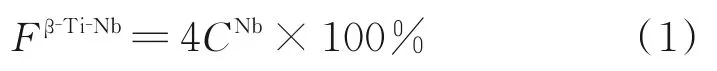
式中,CNb为Nb元素的原子分数。
为了在二维元胞空间中呈现出Ti-2Nb合金β相固溶时相结构单元的数量及其分布,利用式(1)给出的β-Ti-Nb相结构单元的可能份额,计算元胞空间Nx×Ny中β相可能形核点数目Nβ-Ti-Nb(不考虑温度的影响),其计算公式为:式中,数字50表示100个原子形成β-Ti体心晶胞的数目;Nx为元胞空间中x方向单位元胞的个数;Ny为元胞空间中y方向单位元胞的个数。
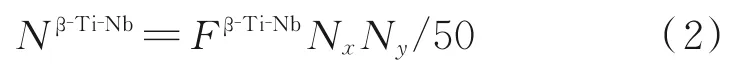
在β-Ti-Nb相结构单元形成的有利形核点中,因固溶加热产生的热振动能够引起有利形核点发生解体与原子扩散,并失去提供β相固溶体有利形核的作用,而有些β-Ti-Nb相结构单元能够抵抗热振动破坏,并且能够形核长大形成典型的β相组织。这些能够抵抗热振动破坏并起到形核作用的相结构单元数量与固溶温度有关,也与β-Ti-Nb相结构单元结合能大小有关。利用β-Ti-Nb相结构单元结合能建立不同固溶温度下β-Ti-Nb结构单元在元胞空间Nx×Ny中的形核点数目Sj,其计算式为:

式中,Kp为经验参数,取值1 330;T为固溶温度,K;Ec为β-Ti-Nb结构单元结合能,取值466 kJ/mol;R为摩尔气体常数,8.314 kJ/mol。
β晶粒长大是集热激活、扩散与界面反应于一体的物理冶金过程,主要表现为晶界的迁移。根据式(3)可以计算不同固溶温度下的形核点数目。然后,按照元胞自动机四邻居规则演构出细小晶粒(见图1中e),这些细小晶粒按照八邻居规则进行吞并、长大(见图1中f)。将上述建模方法编制成计算机软件,在软件中输入元胞空间大小、形核点数目、模拟步长等参数,便可模拟Ti-2Nb合金β相组织。
2 结果与讨论
2.1 不同固溶温度的β相组织模拟
Ti-2Nb合金的名义成分见表1。
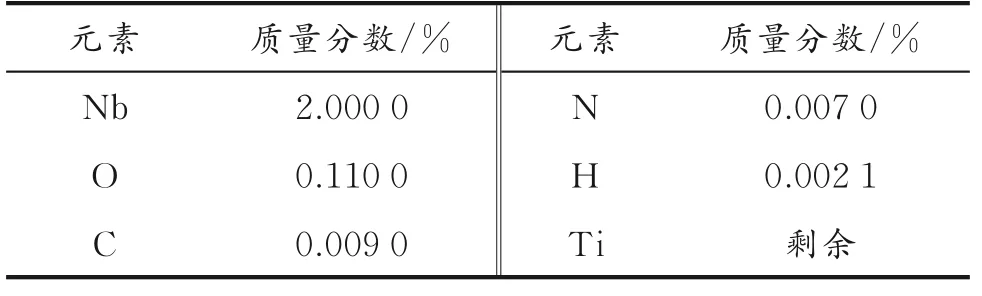
表1 Ti-2Nb合金的名义成分
根据表1给出的Ti-2Nb合金名义成分,计算可得Nb的原子分数CNb为1.04%。将Nb原子分数代入式(1),可得β-Ti-Nb结构单元的可能份额Fβ-Ti-Nb,其值为4.16。本文选取元胞空间50×50,将得到的Fβ-Ti-Nb值代入式(2),可求得β相中形核点数目(不考虑温度影响),其值为208。将不考虑温度的形核点数目及固溶温度代入式(3)中,可求得Ti-2Nb合金在1 000、1 050、1 100、1 150、1 200℃固溶时的β-Ti-Nb结构单元的形核点数目,其值分别为208、200、193、187、181。将计算所得形核点数目(考虑固溶温度因素)及模拟步长(以模拟步长600为例)输入模拟程序中,便可得不同固溶温度下的β相组织模拟图,结果如图2所示。
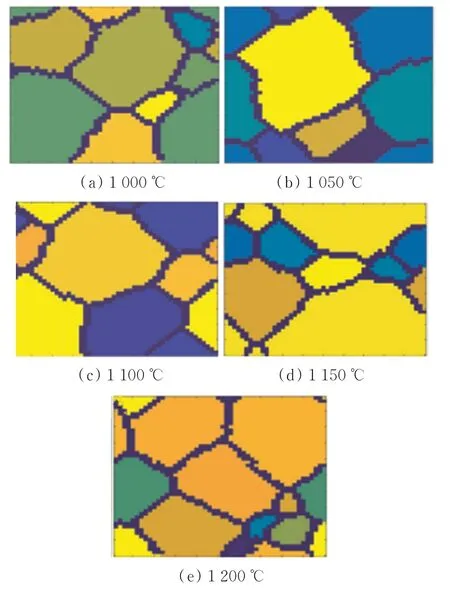
图2 不同固溶温度的β相组织模拟图
从图2可以看出,在模拟步长600下,固溶温度对β相组织的影响并不十分明显,这主要是因为晶粒中组织大小不均匀,差别较大。为便于对晶粒大小进行对比,采用线性截距法统计组织模拟图的平均晶粒尺寸。具体做法为:在组织模拟图1/2y轴处统计沿x轴方向上每个晶粒占有元胞数目。
在模拟步长为600、固溶温度不同的条件下,β相组织的平均晶粒尺寸如图3所示。图3中,平均晶粒尺寸的单位U.G-C.N代表单位晶粒所占的元胞数(模拟平均晶粒尺寸)。
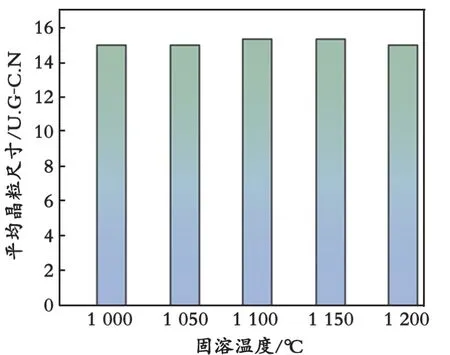
图3 在模拟步长为600、固溶温度不同的条件下,β相组织的平均晶粒尺寸
从图3可以看出,在模拟步长为600、固溶温度不同的条件下,β相组织具有基本一致的平均晶粒尺寸。
2.2 不同固溶时间的组织模拟
在同一固溶温度下,固溶时间对晶粒形态、晶粒尺寸等也会产生影响。固溶时间对微观组织的影响主要通过模拟步长来实现。
不同固溶温度下β相组织平均晶粒尺寸随模拟步长的变化趋势如图4所示。
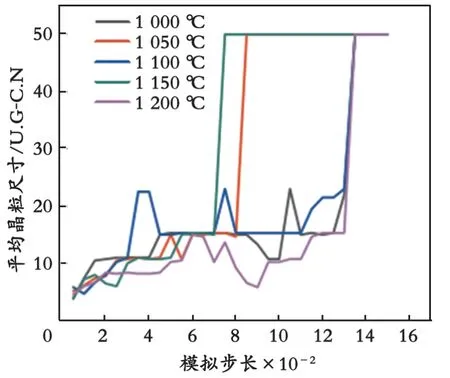
图4 不同固溶温度下β相组织平均晶粒尺寸随模拟步长的变化趋势
从图4可以看出,在不同的固溶温度下,当模拟步长较小时,平均晶粒尺寸总体趋势随模拟步长的增加而增大;当模拟步长较大时,平均晶粒尺寸随模拟步长的增加而呈现不变或波动变化;在每个固溶温度下均出现晶粒急剧增大的现象。造成这一现象的原因可能是:当只有几个大晶粒时,模拟步长对晶粒个数的影响较小,落在平均晶粒尺寸统计线上的晶界长度稳定,平均晶粒尺寸基本保持不变;随着模拟步长的增大,晶粒间会发生吞并,此时平均晶粒尺寸会随着发生突变,晶粒尺寸呈现急剧增加的现象。由此可知,不同固溶时间下组织的演变可以通过模拟步长的变化来体现。
固溶温度为1 000℃时,不同模拟步长的β相组织模拟图如图5所示。从图5可以看出,随着模拟步长的增加,β模拟组织的晶粒逐渐增大,这一结果与图4中的趋势基本相符。
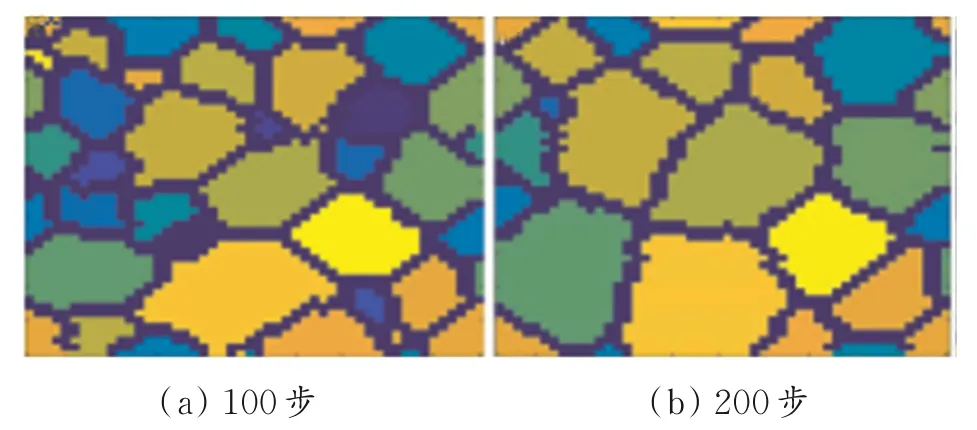
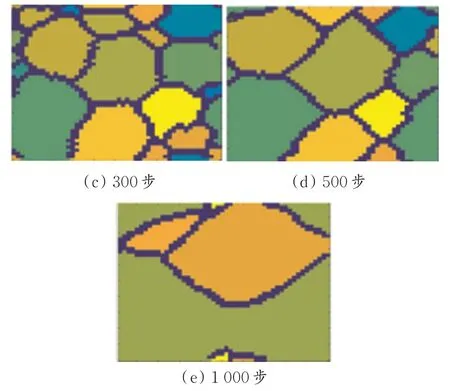
图5 固溶温度为1 000℃时,不同模拟步长的β相组织模拟图
2.3 实际组织与模拟组织的关联方法
β相固溶组织模拟图显示的是抽象的几何图案,为了和实际组织进行联系,提出了模拟组织与实际组织的关联式:
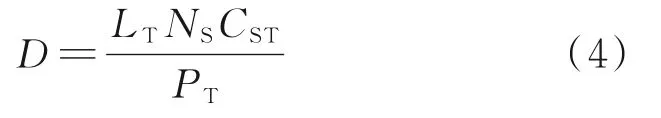
式中,D为模拟计算的晶粒尺寸;LT为实际组织按照标尺折算的总长度;NS为元胞空间内平均晶粒尺寸(按元胞个数进行统计);PT为实际组织图像的像素;CST为元胞空间中单元格点与实际组织的换算系数,可通过元胞空间大小和实际组织像素获得。
以光学显微镜Olympus的金相组织为例,给出模拟组织与实际组织的关联方法。选取Olympus光学显微镜的像素为4 912×3 684,金相组织标尺为200 μm(50倍)。假定Ti-2Nb合金在1 000℃下β相组织的实测晶粒尺寸为446.299 μm。通过式(4)及Image J软件,可以获得1 000℃固溶温度、不同模拟步长下模拟组织的平均晶粒尺寸(实际平均晶粒尺寸),结果如图6所示。
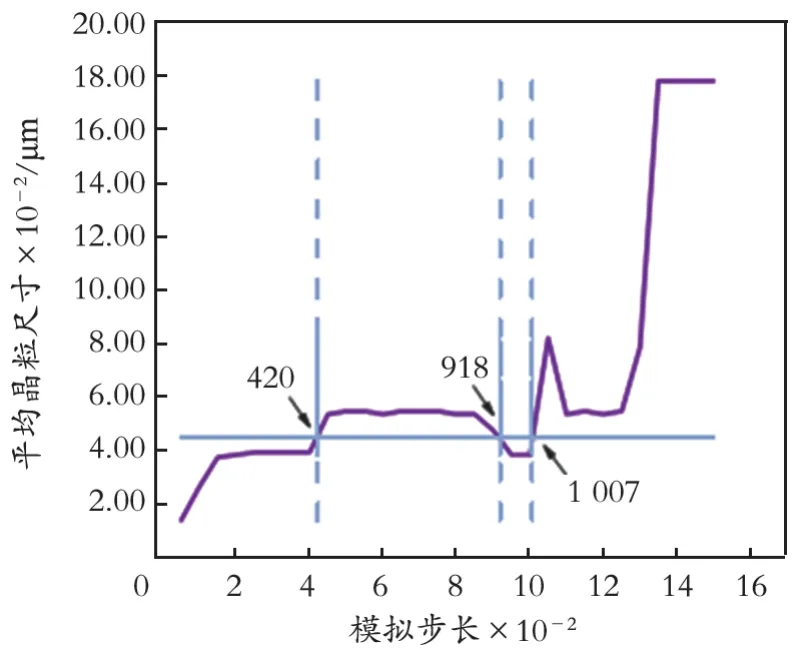
图6 固溶温度1 000℃、不同模拟步长下与实际金相对应的β相组织平均晶粒尺寸
利用该变化趋势图,可以获得与实测值符合的模拟步长,然后将模拟步长输入到计算机软件中,便可获得与实际符合的模拟组织图。具体做法如下:在图6的y轴上找到446.299 μm,然后沿着x轴方向画一水平线,水平线与晶粒变化曲线相交点即为与实际相符合的模拟步长,即420、918和1 007。将获得的模拟步长输入到计算机软件,便可获得与实际金相组织相对应的Ti-2Nb合金模拟组织图,结果如图7所示。从图7可以看出,尽管模拟步长420、918与1 007的平均晶粒尺寸相同,但是组织模拟图相差比较明显,模拟步长越大,组织模拟图中晶粒越不均匀。这进一步表明,模拟步长大时晶粒吞并趋势比较明显。实际上,在合金中观察的金相组织在不同区域内也是有明显差异的。
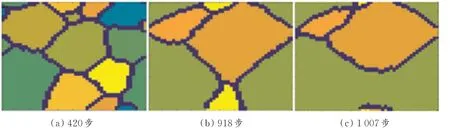
图7 1 000℃下的β相组织模拟图
3 结论
(1)将余氏理论与元胞自动机规则结合,建立了基于余氏理论及元胞自动机的Ti-2Nb合金β相组织模拟方法。
(2)结合余氏理论,建立了β相组织形核点与固溶温度的定量关系式,并建立了模拟晶粒尺寸的描述公式,为后续利用晶粒尺寸将固溶时间与模拟步长间建立定量关系提供了可借鉴的思路。
(3)将余氏理论与元胞自动机规则结合,对1 000、1 050、1 100、1 150、1 200℃下的Ti-2Nb合金β相组织进行了模拟,并给出了模拟组织与实际金相组织的关联方法。

