带有尖角基体上异质形核能力的研究
刘庆辉,李向明
(1.唐山师范学院 数学与信息科学系,河北 唐山 063000;2.昆明理工大学 材料科学与工程学院,昆明 650093)
金属的凝固是金属由液态向固态的相变过程,在大多数情况下,是晶粒形核和生长的过程,其中形核是结晶相变过程的初始阶段[1—3]。形核有均质形核和异质形核两种方式,由于金属液体中总是含有大量的杂质颗粒,晶核往往优先依附于这些杂质的表面而形成。另外,为了控制形核和提高材料的性能,经常向金属液体中加入一些细小的形核剂,使其在金属液体中形成大量分散的人工制造的晶核,因此,异质形核是形核的主要发生形式[4]。研究发现,内部杂质或者外加形核剂的几何特性和材料属性(润湿角)在很大程度上影响其异质形核的能力[5—7],这方面一直是晶体生长理论研究的重点。Volmer M.和Flood H.首先研究了在平面基体上形成球冠状晶核的异质形核问题[8—9];由于理想平整的基体几乎是不存在的,所以在此基础上,Fletcher N.H.考虑了基体是凸球面(悬浮粒子)的情形[10];Qian和Ma研究了凸球面和凹球面上的异质形核[11—12];Lu J.F.,Leung S.N.和Li X.M.等给出了锥形腔内的异质形核机制[13—15];Zhang H.W.和Li Y.X.以熔体中均质形核、夹杂物的平表面以及圆锥形凹坑 3种典型模型对气泡形核机理进行了理论分析[16]。最近笔者分别研究了具有尖点且表面为等曲率的孔洞以及具有变曲率表面基体上的异质形核问题[17—18]。
上述研究工作主要是考虑在坩埚或者模具壁表面的凸起或凹陷处的异质形核问题,通过在其表面形成球冠状晶核来分析形核规律。然而,在坩埚或者模具壁表面可能还存在一些较大的刻痕或者裂缝,当在这类基体上形核时,如果仍采用球冠状晶核模型便不太符合实际,因此需要考虑在基体表面形成其他非球冠状的晶核,目前,对这方面的研究相对较少。文中假设形核基体是一个具有尖角的凹槽,凹槽表面分别为平面、圆柱面和椭圆柱面,考虑晶核从尖角的顶点开始均匀生长,并形成圆柱状晶核,基体的几何特征(尺寸、形状)对其形核能力的影响规律是研究的重点。
1 数学模型
在异质形核过程中,当晶核依附在基体表面形成并达到平衡状态时,3种表面张力及润湿角在交点处满足 Young's方程,即γαs-γns=γnαcosΦ,其中Φ是润湿角,γnα,γns,γαs分别是晶核和母相、晶核和基体以及母相和基体之间的界面张力。根据经典形核理论,如果可以求出晶核的体积V,晶核与母相的接触面积Anα以及晶核与基体的接触面积Ans,那么形成一个异质晶核所需要的形核功W便可以表示为[15,17—18]:

式中:Δµ=µn-µα是在常温常压下,晶核与母相之间化学势的差;Vm是晶核的摩尔体积。
带尖角基体上异质形核截面见图1,考虑形成半径为r,高为h的圆柱状晶核,由于形核功与晶核的高度成正比,为简化运算,令h=1。根据式(1),可以建立形核功的数学模型,计算临界形核功,通过分析异质形核与均质形核临界形核功的比值,即形状因子F的变化规律,得到形核基体的几何特征和材料属性对临界形核功的影响规律,揭示异质形核规律,为更好地控制形核提供理论依据。

图1 带尖角基体上异质形核截面Fig.1 Cross section of heterogeneous nucleation on substrate with sharp corner
1.1 带尖角平面基体上异质形核
首先考虑基体表面是理想化的平面。如图1a所示,假设两个平面之间的夹角,即基体尖角等于2θ,根据几何知识,晶核的体积V、晶核与母相的接触面积Anα以及晶核与基体的接触面积Ans分别为:
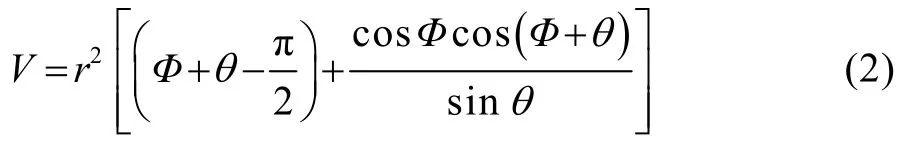
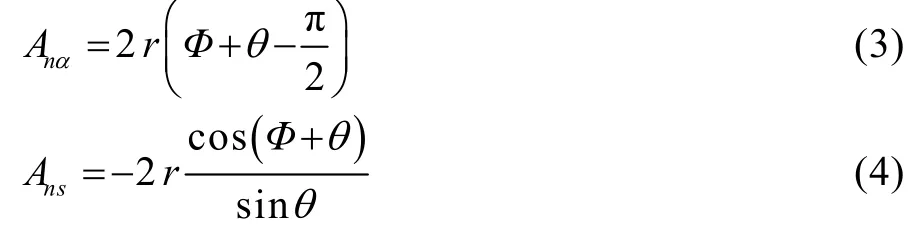
式中:Φ和θ满足:。将式(2)—(4)代入到式(1)中,得到在带尖角平面基体上形成圆柱状晶核所需的形核功:



1.2 带尖角圆柱面基体上异质形核
在实际中,基体表面有可能会出现弯曲的情况,因此,在图1b中,假设基体表面为两个对称且半径为a的圆柱面,基体尖角为两个圆柱面在尖点处切线之间的夹角,设为2θ,为了简化计算,引入中间变量α,即圆柱面在交点处的切线与弦之间的夹角,则晶核的体积V、晶核与母相的接触面积Anα以及晶核与基体的接触面积Ans的表达式为:

其中Θ=Φ+2α+θ,α满足式(9)。

根据式(6)—(9)和式(1),得到在带尖角圆柱面基体上形成圆柱状晶核所需的形核功:
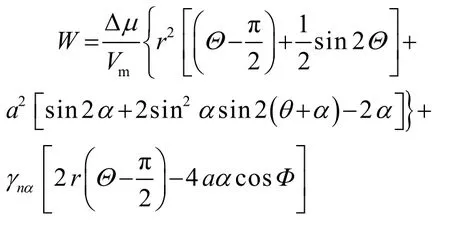
此时,临界形核半径r*仍等于,相应的临界形核功:

上式中形状因子计算如下:

1.3 带尖角椭圆柱面基体上异质形核
虽然带尖角的平面基体和圆柱面基体形状不同,但有一个相同点,就是沿晶核生长的方向,其表面曲率都是恒等不变的。如果基体表面的曲率是连续变化的,那么形核规律又是如何呢,这里考虑一个特殊的变曲率曲面,即基体表面是两个对称且长轴(或短轴)在同直线上的椭圆柱面,正如图1c所示,假设椭圆柱面的半径分别为a和λa(λ>0),基体尖角等于2θ。显然,λ,θ决定了基体的几何形状,且沿晶核的生长方向,当λ>1时,表面曲率是逐渐增加的;当λ<1时,表面曲率是逐渐减少的;当λ=1时为圆柱面,表面曲率不变,恒等于1/a。
由于V,Anα,Ans很难仅通过a,λ,r,Φ和θ来表示,因此,在晶核与基体的交点处,引入中间变量β,即椭圆柱面在交点处的切线与中垂线之间的夹角。经过数学推导,得到晶核体积V、晶核与母相的接触面积Anα以及晶核与基体的接触面积Ans的表达式为:

中间变量β满足方程:

根据经典形核理论,在晶核的生长过程中,只有当晶核半径r随着晶核体积V的增大而增大时,才可以通过r来得到形成稳定晶核的临界条件,因此,结合式(10)和式(13),r对V求导得到:

经过分析,对于固定的Φ∈(0,π),仅当θ接近时,f(β)在内才有可能出现零点。然而,对于有意义的任意Φ,θ和λ,g(β)在内恒大于 0。这就意味着晶核半径r并不总是随着晶核体积V的增大而增大。也就是说,不能简单地使用晶核半径r来表示晶核的长大与缩小。注意到,所以。即在晶核的生长过程中,中间变量β总是随着晶核体积V的增大而增大,因此可以考虑使用β来刻画晶核的生长,并得到形成稳定晶核的临界条件。
将式(10)—(12)代入到式(1)中,得到在带尖角椭圆柱面基体上形成圆柱状晶核所需的形核功:

由式(13)和式(14)可以看出,形核功W是β的函数,如果函数W(β)存在极大值,则该极大值便是形成临界晶核所需的临界形核功,且相应的极大值点便是形成稳定晶核的临界条件,因此,W对β求导,并且使其等于0,则

因为g(β)恒大于 0,所以式(15)存在非零解β*,且满足方程:
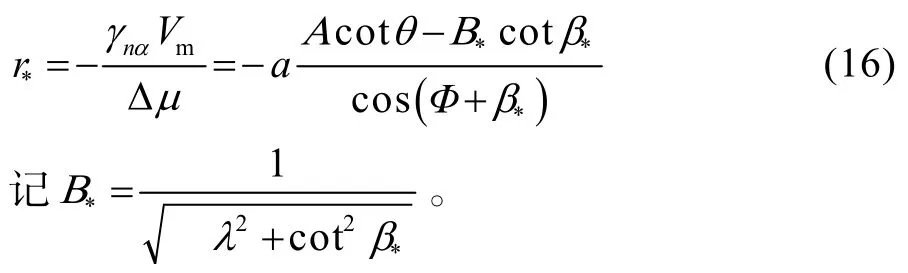
W对β求二阶导数,并将β*代入,得到:

显然,如果f(β*)>0,则W在β*处取极大值;如果f(β*)<0,则W在β*处取极小值。

图2 r与β的关系Fig.2 Relationship betweenr andβ
值得注意的是,如果临界形核半径相对于带尖角椭圆柱面基体的几何尺寸较小,比如在图2中,当r*/a小于函数r(β)的极小值时,式(17)必存在唯一解β*,且为函数W(β)的唯一极大值点,因此β*成为形成稳定晶核的临界条件,即当β>β*时,晶核可以稳定的连续生长。与β*相对应的晶核体积V*称作临界形核体积。由式(16)可以看出,当出现二次形核时,临界形核体积将会有两个,但临界形核半径是唯一不变的。特别地,当在3种不同形核基体上异质形核时,临界形核半径恒等于均质形核时的临界形核半径。
将β*代入到式(14)中,得临界形核功:

其中形状因子:

2 分析和讨论
上一部分讨论了在具有3种不同表面(平面、圆柱面、椭圆柱面)且带有尖角的基体上,形成圆柱状晶核的异质形核问题,根据经典形核理论,建立了形核功的数学模型,得到了与均质形核临界形核功的比值,即形状因子F的表达式。显然,F决定了在基体上形核的难易程度,F越小,越容易形核;反之,越难。下面就来分析形核基体的几何特征(尺寸、形状)和材料属性(润湿角)对F的影响规律。
在带尖角平面基体上异质形核时,形状因子F1与Φ和θ的变化关系见图3。显然,当θ=0.5π时,对应平面基体上的异质形核。如图3所示,当θ固定时,F1随着Φ的增加而增加,说明润湿角越小,平面基体越容易形核,促进形核的能力越强。另一方面,对于固定的Φ来说,F1与θ的变化相对比较复杂。由于,且Φ+θ>0.5π,所以,当Φ≤0.5π时,有F1θ>0,即F1随着θ的增大而增加,而当Φ>0.5π时,F1θ在(0,0.5π)内存在唯一零点θ=-arcsincosΦ,且F1在(0,-arcsincosΦ]内单调减少,在[-arcsincosΦ,0.5π)内单调增加,因此,当润湿角为锐角时,尖角越小,带尖角平面基体的形核能力越强,与平面基体相比,在带尖角平面基体上更容易形核。当润湿角为钝角时,则存在一个最佳尖角,此时基体的形核能力最强,且最佳尖角随着润湿角的增加而增大,如果偏离最佳尖角太多(无论增大还是减小),都将降低带尖角平面基体的形核能力。特别地,当润湿角接近π且尖角接近0时,有F1>1,即异质形核临界形核功比均质形核临界形核功还要大,这意味着在具有这样特性的带尖角平面基体上不会形核,换句话说,带尖角平面基体并不总是比平面基体容易形核。

图3 在带尖角平面基体上异质形核时,F1与Φ和θ的关系Fig.3 Relationship betweenF1 andΦ,θ as heterogeneous nucleation on planar substrate with sharp corner
当基体表面由平面变为圆柱面时,形核规律会发生什么变化呢?在带尖角圆柱面基体上异质形核时,对于固定的R=10,F2与Φ和θ的关系见图4,对比图3可以发现,在这两种形状不同的基体上形核时,F与Φ和θ的关系变化规律是相似的。对于带尖角圆柱面基体,其形核能力随着Φ的增加而减少。当θ=0.5π时,对应在圆柱体或者具有圆柱体形状的纳米棒上异质形核,与之相比,如果润湿角为锐角,在带尖角圆柱面基体上容易形核。如果润湿角为钝角,在带尖角圆柱面基体上是否更容易形核,还需要考虑尖角的大小,但是当润湿角接近 π且尖角接近0时,在带尖角圆柱面基体上显然较难形核,甚至不能形核。

图4 在带尖角圆柱面基体上异质形核时,F2与Φ和θ的关系(R=10)Fig.4 Relationship betweenF2 andΦ &θ as heterogeneous nucleation on cylinder substrate with sharp corner for the case ofR=10
一般来说,当内部杂质或者外加形核剂的几何尺寸越大,其形核能力越强,那么对于带尖角圆柱面基体来说,是否也符合这个规律呢?图5给出了在带尖角圆柱面基体上异质形核时,F2和R的关系。可以看出,当Φ=0.8π,θ=0.15π时,F2随着R的增大而增大,特别地,当R>18时,有F2>1,而对于其他情形,随着R的增大,F2都是减小的。容易证明,当R→+∞时,带尖角圆柱面基体上的异质形核将退化为带尖角平面基体上的异质形核,因此,如果润湿角为锐角,或者润湿角为钝角且尖角较大,则带尖角圆柱面基体的几何尺寸越大,越容易形核,但带尖角平面基体的形核能力更强。如果润湿角接近π且尖角接近0,情况相反,此时为了使带尖角圆柱面基体能够有效促进形核,其几何尺寸存在最大值。也就是说,对于带尖角圆柱面基体,并不是尺寸越大越容易形核,同时还需要考虑润湿角和尖角的大小。

图5 在带尖角圆柱面基体上异质形核时,F2与R的关系Fig.5 Relationship betweenF2 andR as heterogeneous nucleation on cylinder substrate with sharp corner
通过1.3小节中的讨论可知,在带尖角椭圆柱面基体上异质形核时,如果θ接近 max{ 0.5 π-Φ,0} 且λ>1,则对于某些特殊的R,存在二次形核的现象,然而当R较大时,则不会发生。图6给出了当R=10时,F3与λ的关系,可以看出,随着λ的增加,F3都是先减小后增大,需要注意的是,当Φ=0.4π,θ=0.15π时,曲线在[1,10]上看似趋于水平,但实际上是略有增加的,这说明当带尖角椭圆柱面基体的几何尺寸a相对于临界晶核半径r*较大时,存在一个最佳的λ*,满足方程:F3λ(R,λ,Φ,θ)=0,此时最有利于形核,而且当θ接近0.5π时,有λ*<1。
当λ=1时,对应在带尖角圆柱面基体上的异质形核,相比之下,在带尖角椭圆柱面基体上是否更容易形核,取决于λ的选取。假设λ=λ0和λ=1是F3的等值点,即F3在λ0和1处的取值相同,则具有这两种几何特性的带尖角椭圆柱面基体的形核能力是相同的,因此,当λ介于λ0和1之间时,在带尖角椭圆柱面基体上容易形核,反之则较难。值得注意的是,当λ→0时,对所有的θ,曲线都汇聚于一点,此时退化为在平面基体上的异质形核,与之相比,仅当Φ接近π,θ接近0且λ较大时,在带尖角椭圆柱面基体上较难形核。

图6 在带尖角椭圆柱面基体上异质形核时,F3与λ的关系Fig.6 Relationship betweemF3 andλ as heterogeneous nucleation on elliptical cylinder substrate with sharp corner
特别地,在图6a中,对于λ=9,当θ=0.3π,0.4π时,F3没有值,在图6b中也有类似的现象,这意味着,若想使得带尖角椭圆柱面基体具有促进异质形核的能力,那么λ存在最大值,且该最大值随着尖角的增大而减小。
图7给出了在带尖角椭圆柱面基体上异质形核时,F3与θ的关系。可以看出,对于固定的λ,当Φ≤0.5π时,F3随着θ的增大而增大。当Φ>0.5π时,F3随着θ的增大先减小后增大,特别地,如果θ接近0,则F3的值可能大于1,即较小的尖角不利于带尖角椭圆柱面基体形核,这与在带尖角平面基体和圆柱面基体上异质形核的规律相同。另外,在图7中,当R=+∞时,对应在带尖角平面基体上的异质形核。显然,如果润湿角为锐角,或者润湿角为钝角且尖角较大时,在带尖角平面基体上容易形核。如果润湿角为钝角且尖角接近0,则在带尖角椭圆柱面基体上容易形核。由图6和图7还可以看出,带尖角椭圆柱面基体的形核能力随着润湿角的增加而减小。
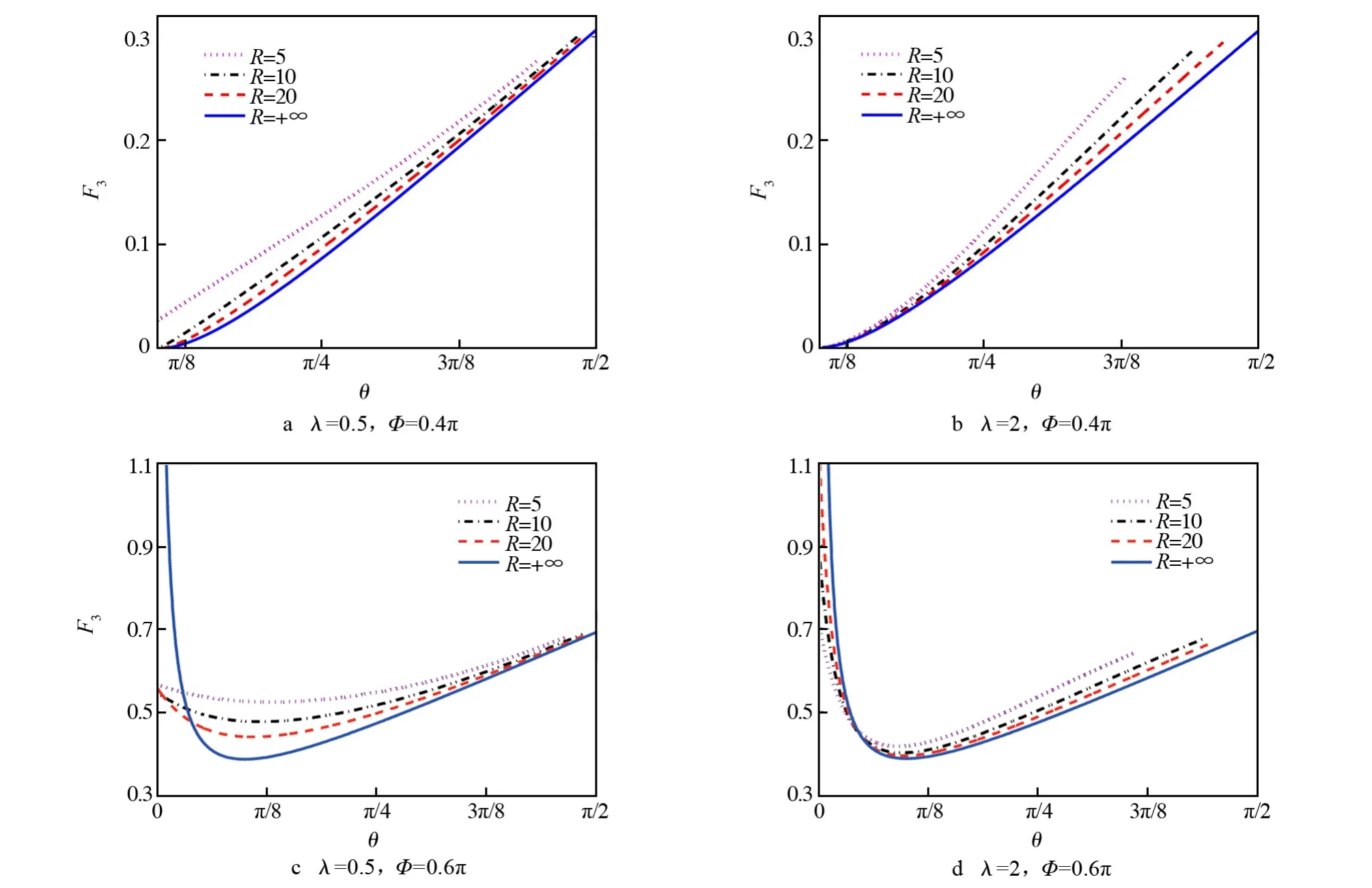
图7 在带尖角椭圆柱面基体上异质形核时,F3与θ的关系Fig.7 Relationship betweenF3 andθ as heterogeneous nucleation on elliptical cylinder substrate with sharp corner
3 结论
研究了在具有3种不同表面(平面、圆柱面、椭圆柱面)且带有尖角的基体上,形成圆柱状晶核的异质形核问题。通过建立形核功的数学模型,分析了基体的几何尺寸a,几何形状λ、θ以及材料属性Φ对其形核能力的影响规律。主要结果如下。
1)当Φ≤0.5π时,基体形核能力随着θ的增大而减小;当Φ>0.5π时,随着θ的增大先增加后减小,此时存在最佳尖角,形核能力最强。特别地,当Φ接近π且θ接近0时,在基体上不会形核,也就是说,对于某些具有特殊几何特征的形核基体来说,即使存在于金属熔体中,也不会起到促进异质形核的作用。另外,Φ越小,基体形核能力越强。
2)当Φ≤0.5π,或者Φ>0.5π且θ较大时,带尖角平面基体形核能力最强,带尖角椭圆柱面基体次之,平面基体最弱。而当Φ>0.5π且θ接近0时,与带尖角平面基体相比,在带尖角椭圆柱面基体上容易形核;且当λ较大时,带尖角椭圆柱面基体的形核能力反而弱于平面基体,甚至不能形核。
3)当带尖角椭圆柱面基体的几何尺寸a相对于临界晶核半径r*较大时,存在最佳的λ*,此时基体具有最强的形核能力,如果偏离太多,将降低形核的有效性,与带尖角圆柱面基体相比,在带尖角椭圆柱面基体上是否容易形核与λ的选取有关。
4)当θ接近 m ax{ 0.5 π-Φ,0} 且λ>1时,在具有特殊几何尺寸的带尖角椭圆柱面基体上会发生二次形核。
——目镜套筒

