化归转化思想在三角恒等变换题型中的应用
⦿甘肃省庆阳市镇原县第二中学
王 东
1 引言
三角变换中利用化归转化思想将复杂的三角函数问题化为形如f(x)=Asin(ωx+φ)+b简单易求解的函数模型.这类题型的设计往往为以下几种情况:结合三角函数求最大(小)值,利用实际问题构建函数模型解决问题,利用向量的运算求解角度或结合解三角形求边长等.熟记公式并灵活应用是解决此类题型的关键.
2 例题分析
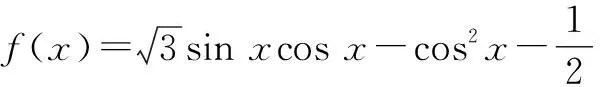
分析:题目中给出的函数名称不同,而且次幂也不相同,所以我们要做的首先就是把高次幂函数降幂,其次把不同名的函数转化为同名函数.这类题型的解题思路就是逆用二倍角公式,结合辅助角公式将函数化归为f(x)=Asin(ωx+φ)+b形式,进而求得函数的最值.

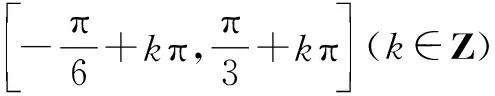
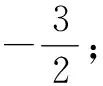

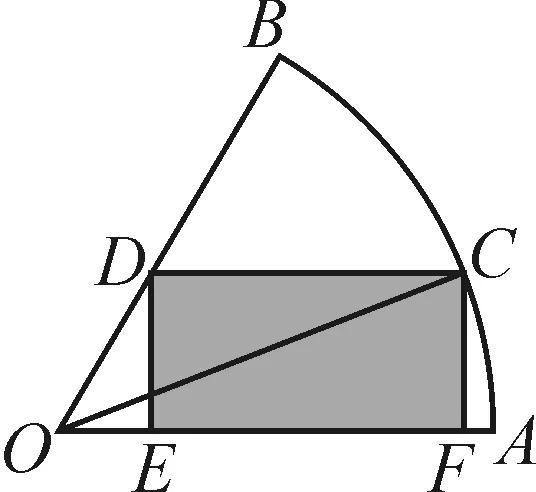
图1
例2如图1,圆心角为60°的扇形AOB的半径为1,C是弧AB上一点,作矩形CDEF,且点D在半径OB上,点E,F在半径OA上.当点C在什么位置时,这个矩形的面积最大?此时∠AOC等于多少度?
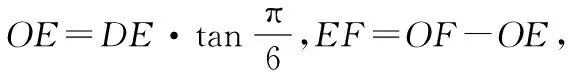
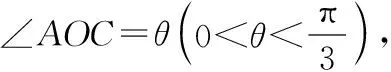
在Rt△FOC中,利用三角函数可得
FC=sinθ·OC=sinθ,OF=OC·cosθ=cosθ.
在Rt△OED中,
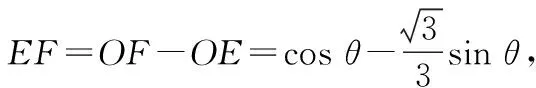
SEFCD=EF·FC
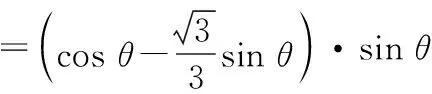
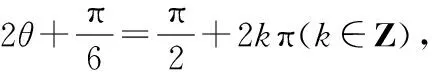
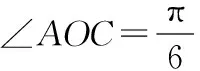
点评:此类题型的新颖之处在于,借助图形利用角的三角函数值表示未知边,通过面积公式构建函数模型,从而利用三角恒等变换解题.
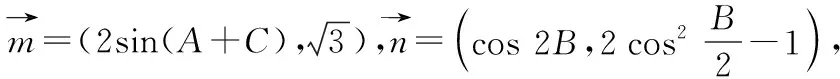
分析:该题中利用两个平行向量的坐标关系建立等式是解题的突破口.利用三角形的内角和等于π这个隐含条件以及角的恒等变换可得sin(A+C)=sinB,再利用二倍角公式和同角的正余弦商的关系,可求得角B的大小.
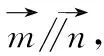
在三角形ABC中,A+C=π-B,所以
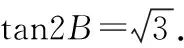
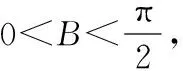
点评:和差角的正余弦公式、二倍角公式等的源头是向量数量积的坐标的运算,所以借助向量的数量积、平行或垂直向量的坐标运算构建三角函数(或方程)模型是比较常见的命题方式,需要同学们构建相应的知识体系.
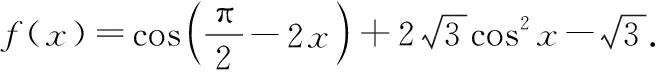
分析:这道题本质在于利用余弦定理解三角形,知道a,c两条边长,只需要借助转化与化归思想化简函数f(x),求得a,c两边的夹角B,就可以利用b2=a2+c2-2ac·cosB,可求得b的值.
解:根据题意,得
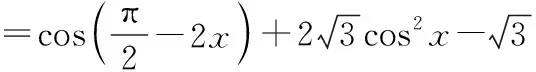
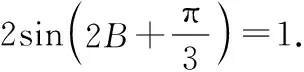
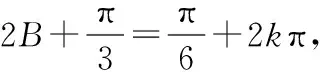
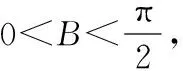
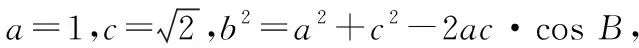
所以,b=1.
点评:在函数模型的应用中求解三角形角度问题,一定要注意对角度范围的讨论,有时还需要进行分类讨论.
3 结束语
解决形如f(x)=Asin(wx+φ)+b的函数模型问题,教学中我们要强化基础知识的记忆——和差角的正余弦公式、二倍角公式、降幂公式以及辅助角公式,并合理利用这些有力工具来提升学生解题的基本技能,在学与练的过程中形成基本活动经验并产生基本思想[2].所以,教师要指导学生对某类题型模型化解题思路的整理,并在解题和应用方面不断灵活“切换”.

