“放缩构造”促进高中数学高阶思维能力提升
⦿江苏省如东高级中学
洪 兵
新一轮高考改革已逐步迈入了推进阶段,加快新课程改革进程,促进新教材的有效使用,发展学生的高阶思维,都是数学教学的重要目标,也是培养学生数学核心素养的重要任务与有力抓手.放缩构造在解题时能力要求较高,若能熟练掌握,必定对学生数学学科核心素养的培养以及高中数学高阶思维能力的提升有较大益处.
1 高中数学高阶思维界定及表现特征
何谓高阶思维?美国教育家布鲁姆 (B.S.Bloom)和加涅等对学习理论进行了高阶思维的划分,将认知领域的教育目标分成识记、理解、应用、分析、评价和创造六个类别.其中分析、评价和创造,通常被称为“高阶思维”,它包括问题解决、推理与决策、批判性思维、创新性思维和反思性思维等五个维度,体现思维的高阶.
高中生在数学学习中培养了较强的实践能力、创新精神,具备高中数学高阶思维,其特征表现为善于发现问题的特殊性.如发现问题的隐含条件等,说明学生养成了求异思维;若能多角度思考分析问题 ,说明学生具备了创造思维;若能灵活妙用数学思想方法,说明学生具有了开放思维.
2 及时发现问题特殊性,培养求异思维
2.1 利用收敛原理,夹逼放缩
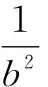
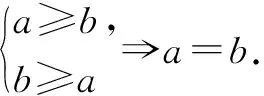
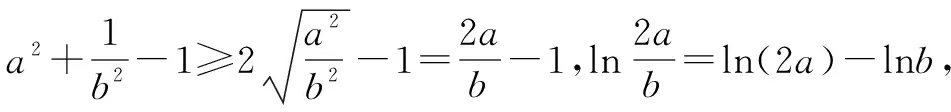
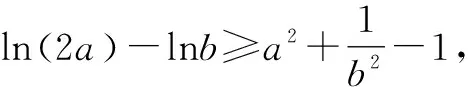
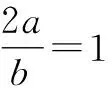
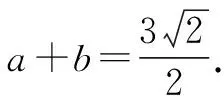
2.2 利用分式形式,极限放缩
问题2已知关于x的不等式a[x-ln(x+1)]≤ex-x-1在x≥0时恒成立,求实数a的取值范围.
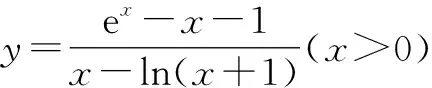
解析:当x=0时,a∈R,则主要研究当x>0时实数a的取值范围.
由x-1≥lnx恒成立可知x≥ln(x+1),所以x>0时,x-ln(x+1)>0.
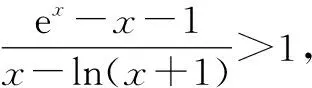
综上可知,实数a的取值范围是a≤1.
3 多角度思考分析问题 ,培养创造思维
3.1 利用分层转化,易元放缩
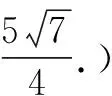
解题思路:利用分割法求四边形ABCD的面积,在两个三角形中分别使用余弦定理,多角度分析简单的几何问题 ,再将所有的关系式互相联系,培养学生的创造性思维.
另外,已知二元变量x,y满足函数t(x,y),先以变量x为主元,令f(x)=t(x,y),求得f(x)=t(x,y)的最值φ(y),再以变量y为主元,求得φ(y)的最大值.利用分层处理,易元放缩,培养学生创造思维,提升数学高阶思维能力.
解析:连接BD,将平面四边形ABCD分割成两三角形.
在△BCD中,有BD2=CB2+CD2-2CB·CDcosC=22+22-2×2×2cosC=8-8cosC.
在△ABD中,有BD2=AB2+AD2-2AB·ADcosA=12+42-2×1×4cosA=17-8cosA.
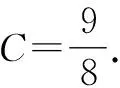
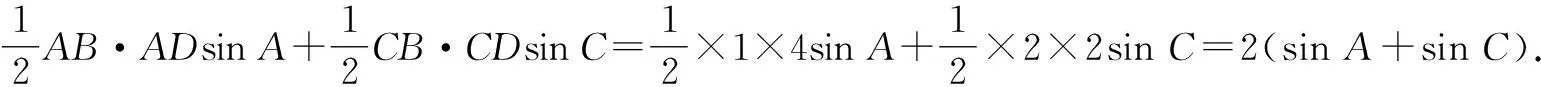
在三角形中,易知A,C∈(0,π),sinA>0,sinC>0.
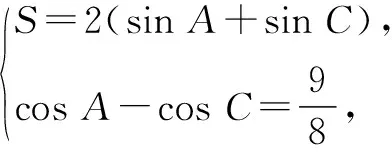
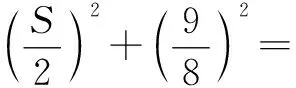
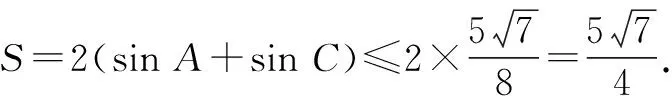
3.2 利用同构特征,单调放缩
问题4(2020年高考山东卷第22题改编)已知函数f(x)=aex-1-lnx+lna,若f(x)≥1,求实数a的取值范围.(答案:[1,+∞).)
解题思路:对于复杂的不等式构造出同构不等式,形如f[g(x)]≥f[h(x)],由函数y=f(x)的单调性,化简得g(x)与h(x)的不等关系式,再研究参数的取值范围.利用整体思想,分层次转化,达到降维的目的.
解析:f(x)=aex-1-lnx+lna=elna+x-1-lnx+lna≥1等价于
elna+x-1+lna+x-1≥lnx+x=elnx+lnx
①
令g(x)=ex+x,①式等价于
g(lna+x-1)≥g(lnx).
显然g(x)为单调增函数,所以lna+x-1≥lnx,即lna≥lnx-x+1.
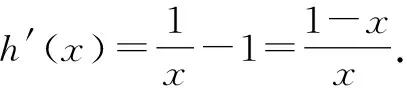
所以,在区间(0,1)上,h′(x)>0,h(x)单调递增;在(1,+∞)上,h′(x)<0,h(x)单调递减.
所以,h(x)的最大值为h(1)=0,即lna≥0,解得a≥1.
故填答案:[1,+∞).
4 灵活妙用数学思想方法,培养开放思维
4.1 利用曲线相切,传递放缩
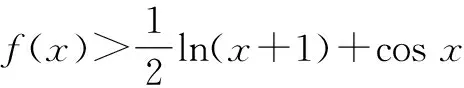
解题思路:此类问题的思考角度很多,从不等式的角度寻求思路繁琐.让学生认真观察提出不同见解,根据图形的特征,灵活妙用数学思想方法,突破思维瓶颈,培养学生开放思维,从而提升数学高阶思维能力.
由函数y=f(x)与y=g(x)图象在点(x0,f(x0))处相切,且f(x)≥g(x0)≥g(x),f(x0)=g(x0) , 则f(x)的最小值为f(x0)=g(x0).
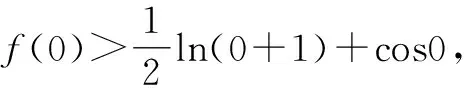
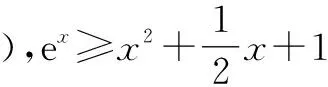
当a>1时,
=1-cosx≥0(x=0取等号).
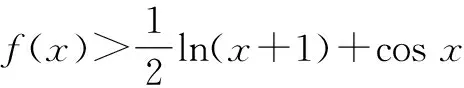
4.2 利用数形结合,几何放缩
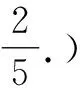
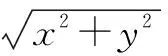
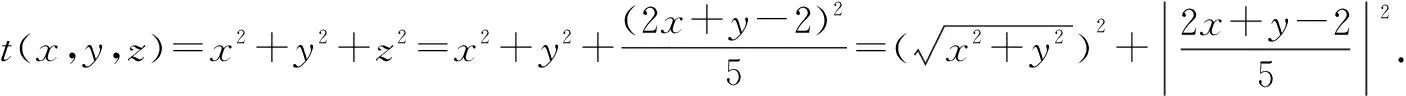
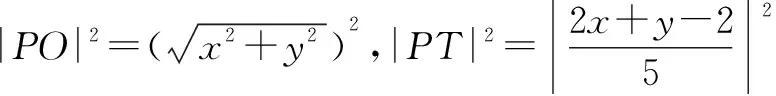
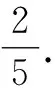
5 结束语
“放缩构造”整合高中数学知识,对应变能力有较高的要求.数学时应抓住题目的特点,根据不同题目的类型,采用恰到好处的放缩方法,特别在不等式恒成立有解求参、不等式放缩证明、函数最值与超越函数间的关系等问题的研究,体现非常充分;教学时应精心设置问题,总结基本的放缩方法和放缩调整手段.鼓励学生积极探究,启发深度思考,激发深度学习.
可见,“放缩构造”可以作为高中阶段提升思维和逻辑推理能力、分析问题和解决问题的能力的支点,探究解决问题的方法和途径.“放缩构造”是积累思维经验的过程,提升学生数学高阶思维能力,从而达到培养学生数学学科核心素养的目的.

