定理结构与图形结构双管齐下自然生成解法——正、余弦定理的几何应用

⦿江苏省苏州市第六中学校

李 娟

1 引言

正、余弦定理揭示了三角形中边、角的量化关系.解三角形是高考必考的知识点，总体难度适中.本文试图从定理本身的结构特征和几何图形的结构、条件和问题整合考虑，阐述如何“快”且“准”地高效运用正、余弦定理.教学结构主义的代表人物布鲁纳强调：就是学习事物是如何关联的，便于学生记忆和正迁移，能使学生提高直觉处理问题的能力.联合考虑问题和条件中的元素，辨别是哪个定理对应的元素，快速识别用单一定理还是“联合行动”抑或“多次行动”.

下面通过具体案例对正、余弦定理的几何应用进行分析.

课前检测给出几道小题，主要复习相关知识与相应的思想方法.

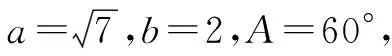
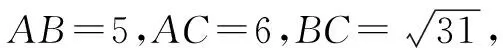
选题目的：第(1)～(3)小题的字母符号与原定理一致，便于学生提取和迁移相关知识.第(4)小题与原定理字母符号不一致，可转化成对应的小写字母，同时引导学生观察余弦定理左右两侧边与角的关系，为在较复杂图形中正确且快速地根据原理“造等式”做准备.在解决上述简单问题时，注意引导学生关注两个定理的“同”与“异”.“同”在正、余弦定理本质是恒等式，因此首要功能是“造等式”，体现方程思想.“异”在元素对象不同，结构特征亦不同.正弦定理实质是3个等式，每个等式中的元素是四个量，即两组对应边、角，其结构特征体现了数学的对称美和和谐美；余弦定理也是3个等式，元素是四个量，即三边一角，而角决定选用3个等式中的哪一个.余弦定理是勾股定理的拓展延伸，注意新知识和旧知识的联系.同时，提醒学生注意应用正弦定理求角时，有一解和两解两种情况需要结合“内角和定理”和“大边对大角，小边对小角”进行检验取舍，而余弦定理求角是唯一解.因此，在有选择的前提下，优选余弦定理求角.正、余弦定理的功能主要是两个方面，即“造等式”和“边角互化”.

2 经典题例，突破问题

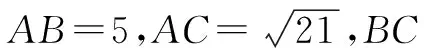
思路探求：本题是正、余弦定理的几何应用，题目中的字母符号与原定理不一致.首先，要求学生明确原定理中的元素对象及其关系，才能正确地“造等式”.其次，题目的顺利解决还需要学生充分了解图形的结构特征，即大三角形分成两个小三角形，两个小三角形有一条公共边、一对互补内角.这些特殊之处就是联系之处，就是架构关系式之处，是解题的关键.另外，没有被切割的∠B，∠C是两个三角形的内角，根据需要选择三角形，一般选择已知条件多的三角形利用定理构造等式(或方程组).根据上述分析，自然生成下面两种解法.

解法1：利用两个小三角形的一对互补角建立等式，两个小三角形内涉及的元素都是三边一角，故都使用余弦定理建立方程.

设BC=2m，则BD=CD=m.

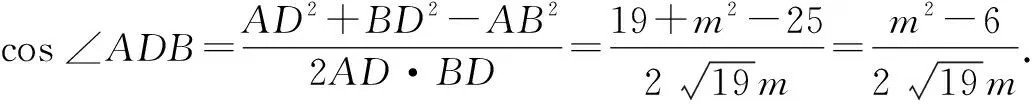
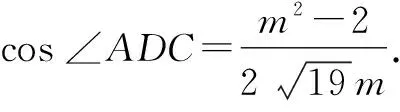
又∠ADB+∠ADC=180°，所以cos ∠ADB+cos ∠ADC=0，即m2-6+m2-2=0.

解得m2=4，m=2，故BC=4.

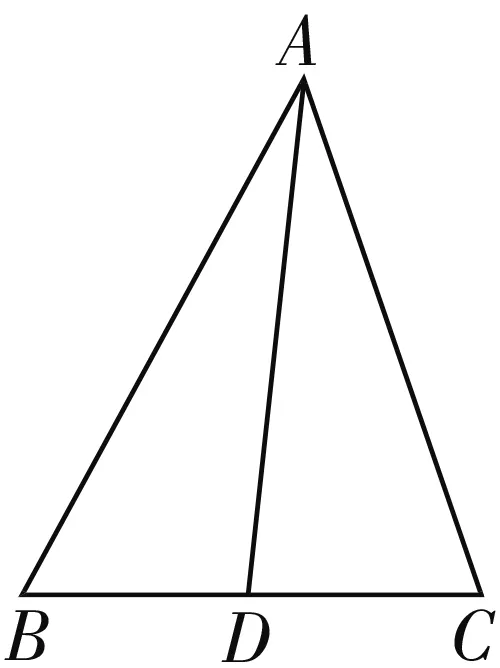
图1

解法2：利用∠B是图1中△ABC与△ABD的内角构建等式，两个三角形内涉及的元素亦是三边一角，故使用余弦定理建立方程.

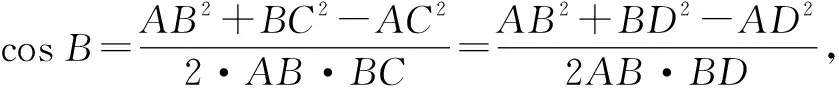
3 侧重综合，关注应用

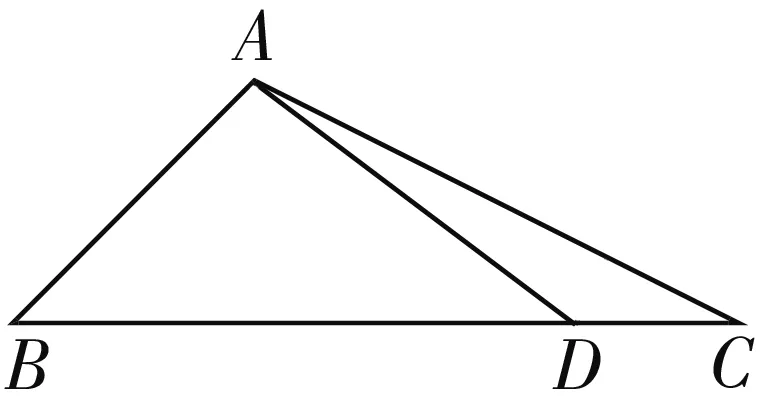
图2

3.1 与三角函数的综合

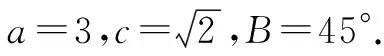
(1)求sinC的值；

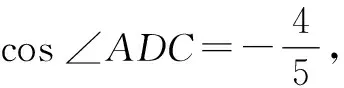
思路探求：(1)图2中的∠C是两个三角形的内角，而△ABC中条件相对充分.梳理题目已知条件可知既不是三边一角，也不是两组对应边、角，因此判断是“联合行动”，先由余弦定理解得边b，再由正弦定理求sinC.当然，亦可由余弦定理解得cosC，再由同角三角函数基式关系式求sinC.

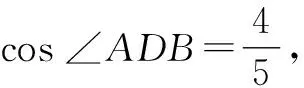
3.2 模块间的联结：与椭圆的综合

例3(2019年高考数学全国卷Ⅰ第10题)已知椭圆C的焦点为F1(-1，0)，F2(1，0)，过F2的直线与C交于A，B两点.若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为( ).

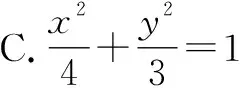
思路探求：本题考查椭圆的几何性质、焦点三角形和余弦定理.对应的图形结构和前面一致，因此构造等式的途径也有3种，下面给出其中一种解法.

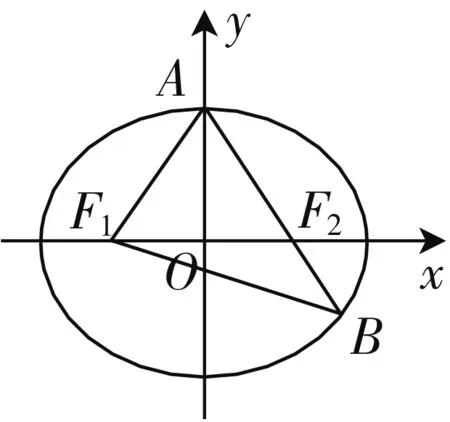
图3

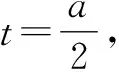
在△ABF1中，由余弦定理得

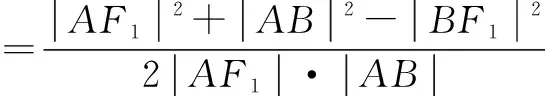
在△AF1F2中，由余弦定理得

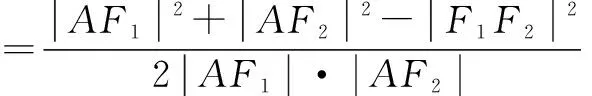
解得a2=3c2.

又c=1，所以a2=3，则b2=a2-c2=2.

4 利用结构特征，巧证明

4.1 证明三角形内角平分线性质定理

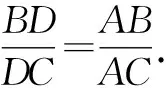
证明：如图4,设∠BAD=∠CAD=α，∠ADB=β，∠ADC=γ，则β+γ=180°.

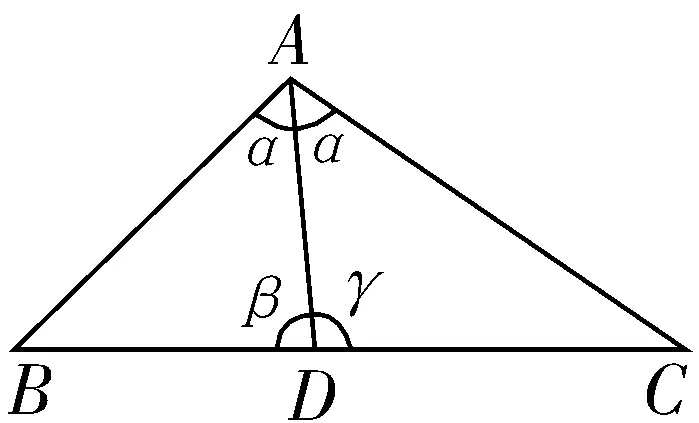
图4

因而sinβ=sinγ.

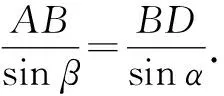
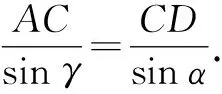
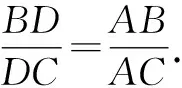
4.2 代数问题几何化，建立三角形几何模型

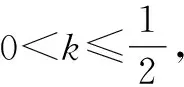
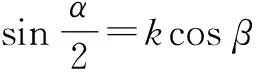
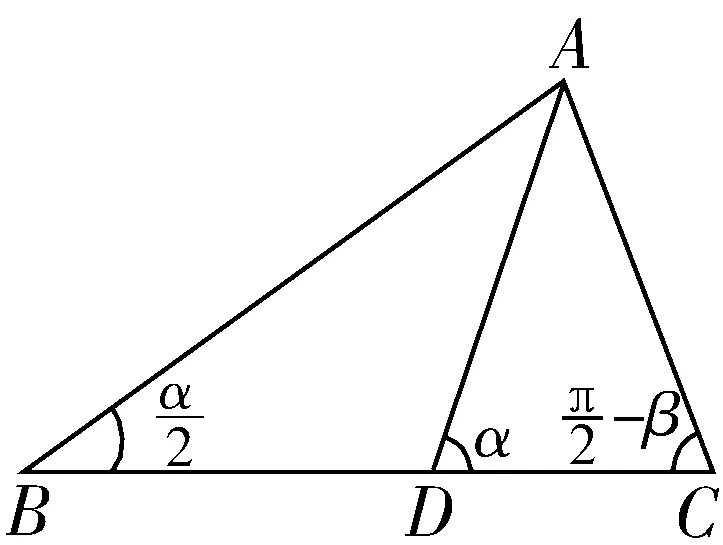
图5

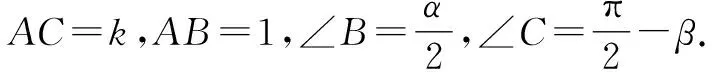
在BC上取点D，使得BD=AD，则∠ADC=α.

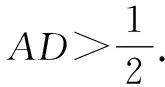
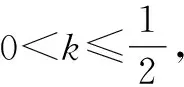
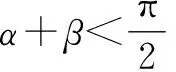
5 结束语

本文主要探讨在所研究的几何模型，即大三角形分割成两个小三角形中，结合图形特征，通过梳理条件、结论中的元素，快速、准确地选用原理构造方程(方程组)，从而解决问题.