高考命题有依据 复习备考有目标

⦿江苏省南京市大厂高级中学

李素娟

1 引言

“立德树人”是历年高考数学命题的指导思想，在这一核心功能指导下，全面贯彻高考评价体系的要求，推动人才培养的改革创新，引领并指导高中数学教育与教学，得以合理选拔高一层次人才.因而，高考数学命题有据可依，试卷必须充分体现数学学科的特点，突出数学必备知识的考查，合理引导教学，倡导育人为本、遵循教育规律、回归数学教材等的落实，为复习备考提供明确的目标.

2 核心素养引领复习方向

培养数学学科核心素养是为了更好地促进学生形成“三观正”(正确的人生观、价值观、世界观)、“用数学”的目的.借助数学的眼光观察世界，发展一般性素养——主要涉及数学抽象、直观想象；借助数学的思维分析世界，发展严谨性素养——主要涉及逻辑推理、数学运算；借助数学的语言表达世界，发展应用性素养——主要涉及数学建模、数据分析.从培养数学学科核心素养角度入手来设置命题，为复习备考指明方向.

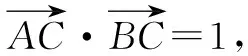
A.圆 B.椭圆 C.抛物线 D.直线

分析：根据题目条件，取平面内的两个定点A，B的极端位置——A，B重合，达到两点合二为一来分析与处理问题，并把特殊情况下得到的结论反馈到题目中去，选择与之相符合的结论，从而得以巧妙逻辑推理，合理破解.破解本题的方法很多，不同方法涉及不同的核心素养与数学知识.

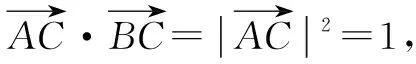
复习备考建议：正确把握高中数学课程标准与教学大纲、高中数学教学、高考数学命题以及数学核心素养等之间的关系，有针对性地安排实例与练习，就六个方面的核心素养借助数学的眼光、数学的思维、数学的语言等视角切入，合理强化训练，落实核心素养的培养.

3 夯实教材为高考筑基

数学教材是历年高考命题之源，典例之根，母题之库.而高考试题主要考查主干知识、能力和素养，侧重于思维、应用、创新，从“解题”上升到“解决问题”，从“做题”升华到“做人做事”，直到提升综合素养.在数学学科素养导向新举措、能力考查新突破的形势下，相当数量的高考试题都能在数学教材中寻觅其“影踪”，找到相关的背景、面孔、变形、拓展与提升等，从回归数学教材角度入手来设置命题，为复习备考提供蓝本.

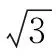
分析：根据题目条件，先确定焦点的坐标，进而确定焦点弦所对应的直线方程，联立直线与抛物线方程，消元后转化为相应的二次方程，结合二次方程的实数根，利用弦长公式加以运算即可确定.

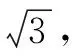
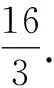
链接教材：

普通高中课程标准实验教科书《数学·选修2-1(A版)》(人民教育出版社，2007年2月第2版)第69页例4：

斜率为1的直线l经过抛物线y2=4x的焦点F，且与抛物线交于A，B两点，求线段AB的长.

复习备考建议：高考命题经常是源于教材意料之外，植于教材情理之中，高于教材能力之上.在复习备考时，充分理解与掌握数学的知识体系、框架结构、公式定理、例题习题等，进一步对教材内容进行组合、加工和拓展，挖掘知识本源，“重视很多习题潜在着进一步扩展其教学功能、发展功能和教育功能的可行性”.

4 高考真题延续往年精髓

往届高考真题已然成为新一届高考命题的一个极佳的“试题库”“题源库”，通过变形、转化、深入、创新、拓展应用等手段加以合理改编，承载指导数学教学与学习中的示范与引领作用.而深入研究往届的一些典型高考试题，对把握高考命题规律，感悟高考热点、重点及其考查方式，探寻培养数学学科素养的途径，提高应考能力和复习效率等都大有益处.从高考真题角度入手设置命题，为复习备考提前演练.

例3(2020年高考数学全国卷Ⅰ理科第14题)设a，b为单位向量，且|a+b|=1，则|a-b|=______.

分析：对条件中平面向量和的模加以平方处理，通过数量积公式的转化与应用，确定对应数量积的值，再通过平面向量差的模的平方处理来转化与运算，进而得以求解.

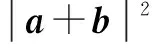
其实该高考命题来源于2004年高考数学全国卷Ⅱ文科第9题.通过两向量a，b的模以及对应平面向量的和(或差)的模来求解相应平面向量的差(或和)的模问题.破解时，可以利用平面向量的数量积公式或坐标法来处理，也可以借助“平行四边形四边的平方和等于两条对角线的平方和”的公式来处理.

高考真题(2004年高考数学全国卷Ⅱ文科第9题)已知向量a，b满足|a|=1，|b|=2，|a-b|=2，则|a+b|=( ).

(答案：D)

复习备考建议：高考复习备考一定要“知己知彼”，才能“百战百胜”.特别是有针对性做一些历年高考中的同一知识点的相关典型实例，从数学知识、数学思想方法与数学能力等角度切入，不断理解并掌握对应的实质，领悟并升华思想方法，挖掘并拓展数学能力，为我所用，融会贯通，真正分享历年高考真题的智慧，不断提升数学能力与核心素养.

5 科学育人巧融高考命题

高考命题倡导“五育”(德智体美劳)并举的根本目标，有效落实“五育”，全面提升人文素养.高考数学试题也经常融入政治经济、科学文化、艺术哲学、道德修养、价值理念等“五育”元素，交汇数学，特别是合理设置创新情境，结合社会现实，贴近生活实际，关注时代热点，充分体现数学实际应用价值以及育人价值.从科学育人角度入手设置命题，为复习备考创设情境.

例4(2020年高考数学全国卷Ⅱ理科第3题，文科第4题)在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成1 200份订单的配货，由于订单量大幅增加，导致订单积压.为解决困难，许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货，预计第二天的新订单超过1 600份的概率为0.05，志愿者每人每天能完成50份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于0.95，则至少需要志愿者( ).

A.10名 B.18名 C.24名 D.32名

分析：结合阅读与理解，通过概率与对应的数据分析，归纳与总结出题目的内涵，合理构建数学模型，合理调配志愿者.

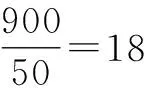
故选：B.

复习备考建议：在复习备考过程中，有针对性结合一些相关“五育”(德智体美劳)实例的问题，通过问题背景的巧妙设置，合理把高考数学与育人根本目标进行有机融合，充分体现高考数学的指导性功能与方向性意义.复习备考关键在于引导学生对问题的理解、分析、剖析、建模等，并结合数学相关知识来进一步融合与深入，拓展数学创新与应用，体现数学特色.

6 结束语

合理借助核心素养引领复习方向，落实命题指导思想；夯实教材只为高考筑基，复习应回归数学教材；高考真题延续往年精髓，要合理应用历年真题；科学育人巧融高考命题，可创新情境巧妙设置.把握改革精神，创新试题设计，优化试卷结构，明确复习方向，全面对学生的数学语言的阅读、理解、转化、表达等能力加以不断深化，紧紧抓住数学基础知识和基本技能，从基础入手，不断深入，有效复习，全面提升.